Dieser Online-Zugkraftrechner bzw. Leistungsrechner kann unter anderem eine der folgenden Größen berechnen: maximal mögliche Geschwindigkeit, erforderliche Leistung & Zugkraft, mögliche Steigung, Anhängelast und erforderliche Haftreibungszahl. Im Anschluss findet man dazu passendes Hintergrundwissen und Formeln.
Mit der Voreinstellung werden die benötigte Leistung und die dafür erforderliche Zugkraft eines Railjets (Elektrolokomotive Taurus 1116 und sieben Wagen) bei einer Geschwindigkeit von 230 km/h berechnet.
Inhaltsverzeichnis
Werbung
Leistungs- und Zugkraft-Rechner für Straße & Schiene
Unter “Vorauswahl” findet man passende Werte für PKW, LKW, Bus, Fahrrad oder Züge.
Standardmäßig werden Motor- und Antriebswirkungsgrad nicht berücksichtigt!!
* Für diese Werte ein Minus vor die Zahl setzen!
Abkürzungen:
| Verz. | Verzögerung |
| Luftwiderstandsbeiw. | Luftwiderstandsbeiwert |
| F. | Faktor |
>> Hier gibt es Zusatzinformationen für die einzugebenden Werte.
Hinweise für die Verwendung des Zugkraftrechners
- Dieser Rechner kann eine der folgenden Größen berechnen:
- Theoretisch maximal mögliche Geschwindigkeit bei gegebener Leistung. Die erreichbare Geschwindigkeit wird allerdings unter Umständen durch die maximale Drehzahl des Motors beschränkt, zudem ist die Leistung nicht über den gesamten Geschwindigkeitsbereich verfügbar.
- Erforderliche Leistung und Zugkraft bei gewünschter Geschwindigkeit. Die zur Verfügung stehende Zugkraft kann aus dem Zugkraftdiagramm abgelesen werden.
- Bewältigbare Steigung
- Vorhandene Beschleunigung
- Mögliche Masse der Wagen
- Masse der Lokomotive
- Zusätzlich kann bestimmt werden:
- Nötige Haftreibungszahl und erforderliche Zugkraft
- Maximal mögliche Anfahrzugkraft aufgrund der Haftreibungszahl, das Triebfahrzeug kann auch über weniger oder mehr Zugkraft verfügen, siehe Tabelle weiter unten.
- Die hier angeführten Haftreibungszahlen gelten nur bei relativ niedrigen Geschwindigkeiten, für Schienenfahrzeuge gilt die Berechnung der Anfahrzugkraft zudem nur bei Verwendung von Stahlrädern auf einer Stahlschiene. Siehe dazu die Unterseite Haftreibungszahlen!
- Die Berechnung für die Anfahrzugkraft gilt nur dann, wenn auf jede Achse ungefähr die gleiche Last wirkt.
- Für die richtige Funktion wird keine Gewähr übernommen – für Berichtigungen und Verbesserungs-Vorschläge bitte um Nachricht mittels Kontaktformular!
Hintergrundwissen und Formeln
Zusatzinformationen zu den einzugebenden Werten
Vergleichswerte für Anfahrzugkraft, Stundenleistung, Masse und µH
Bitte beachten Sie, dass hier die Anfahrzugkraft in kN, die Stundenleistung in kW und die Masse in Tonnen angegeben wird! K ist die Abkürzung für kilo und bedeutet 1000, daher sind 1 kW = 1000 W, 1 kN = 1000 N.
| Beispiele (ÖBB) |
Anfahrzugkraft in kN |
Stundenleistung in kW |
Masse in t |
µH * |
| Lok 1293 | 340 | 6400 | 90 | 0.385 |
| Lok 1016/1116 | 300 | 6400 | 86 | 0.356 |
| Lok 1044/1144 | 327 | 5400 | 84 | 0.397 |
| Lok 2016 | 235 | 2000 | 80 | 0.299 |
| Lok 2043 | 196 | 1104 | 68 | 0.294 |
| Triebwagen 4020 | 117 | 1200 | 129 | |
| Triebwagen 5047 | 68 | 419 | 47 |
Quelle: Wikipedia
* Notwendiger Haftreibungskoeffizient beim Anfahren, berechnet aus den gegebenen Werten.
Zugkraftdiagramm einer modernen E-Lokomotive
In der folgenden Abbildung ist ein sogenanntes Zugkraftdiagramm für eine moderne Elektrolokomotive zu sehen. Es handelt sich dabei um eine schematische Zeichnung, die dem Zugkraftdiagramm der Baureihe 1016 bzw. 1116 (Taurus) der ÖBB jedoch ähnlich ist.
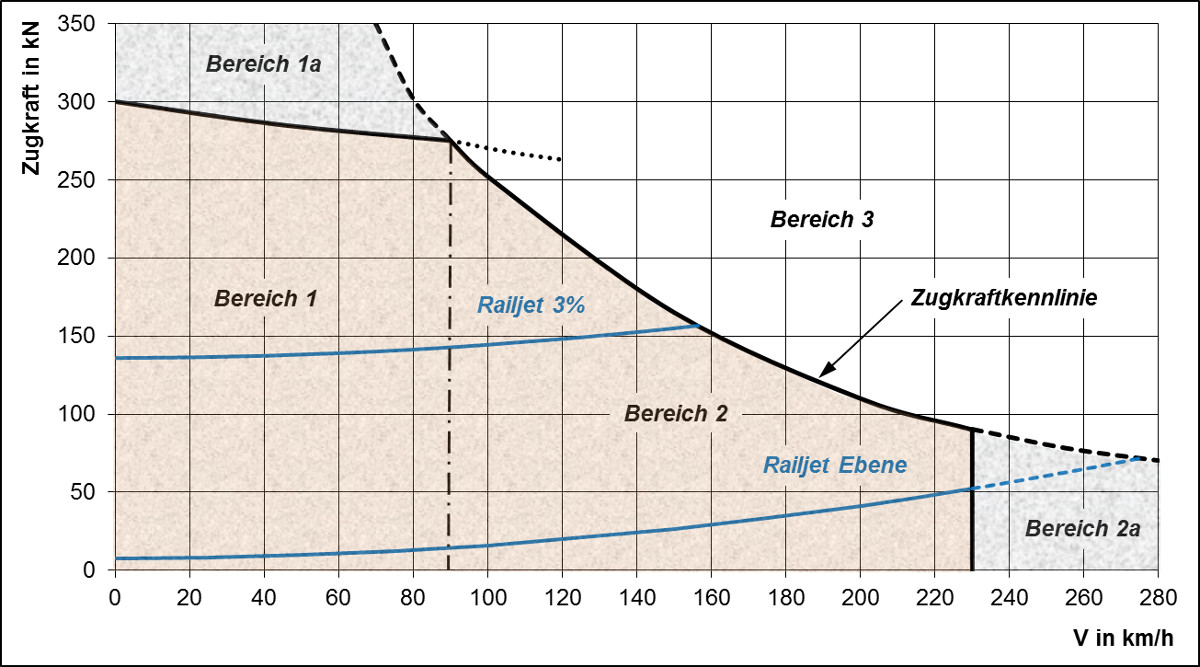
In diesem Zugkraftdiagramm ist folgendes zu sehen:
- Die Zugkraftkennlinie zeigt die maximal vorhandene Zugkraft der Lokomotive in Abhängigkeit von der Geschwindigkeit.
- Das Diagramm besteht aus fünf Bereichen, wobei in der Praxis nur die hellbraune Fläche (Bereiche 1 und 2) von Bedeutung ist:
- Bereich 1: Die auf die Schienen übertragbare Zugkraft wird durch die Haftreibungszahl und nicht aufgrund der zur Verfügung stehenden Leistung beschränkt.
- Bereich 1a: Mit der installierten Leistung wäre eine größere Anfahrzugkraft möglich, das lässt allerdings die Haftreibungszahl nicht zu, die Räder würden schleudern (= durchdrehen).
- Bereich 2: Nur die Leistung der Lok begrenzt die auf die Schienen übertragbare Zugkraft. Hätte die Lokomotive mehr Leistung zur Verfügung, wäre demnach eine höhere Zugkraft möglich.
- Bereich 2a: Die Lok könnte aufgrund ihrer Leistung eine höhere Geschwindigkeit erreichen, die Höchstgeschwindigkeit wird im Planbetrieb jedoch auf 230 km/h beschränkt. Im Jahre 2006 erreichte ein Taurus III 357 km/h, das ist der Weltrekord für konventionelle Lokomotiven.
- Bereich 3: Für eine höhere Zugkraft hat die Lokomotive einfach zu wenig Leistung.
- Als Ergänzung sind noch zwei blaue Kennlinien eingezeichnet, die mit dem Zugkraftrechner bestimmt wurden:
- Railjet 3 %: Diese Kurve zeigt die benötigte Zugkraft eines Railjets (Lok Taurus und sieben Wagen) auf einer Strecke mit einer Steigung von 3 % in Abhängigkeit von der Fahrgeschwindigkeit. Der Zug könnte demnach maximal 155 km/h fahren, in der Praxis würde er jedoch nur mit rund 130 km/h verkehren, da gewisse Reserven nötig sind, beispielsweise bei Gegenwind und für das Beschleunigen.
- Railjet Ebene: Diese Zugkraft braucht ein Railjet in der Ebene.
Berechnung der maximalen Zugkraft = Anfahrzugkraft
Die maximale Anfahrzugkraft, die ein Fahrzeug unter Berücksichtigung der Haftreibungszahl theoretisch erbringen kann, berechnet sich wie folgt:
$$F_{Z.max}=m_{Lok}·g·cos(\alpha)·\frac{Achsen_{angetrieben}}{Achsen_{alle}}·µ_H$$
| FZ.max: | Maximale Zugkraft in N |
| mLok: | Masse der Lok in kg |
| g: | Erdbeschleunigung in m/s² |
| α: | Steigungswinkel in ° (für kleine Winkel wird cos α gleich eins gesetzt) |
| Achsenangetrieben: | Anzahl der angetriebenen Achsen |
| Achsenalle: | Gesamtzahl der Achsen |
| µH: | Haftreibungszahl, siehe auch vorige Tabelle |
Für die Erdbeschleunigung setzt man 9.81 m/s² ein. Wenn alle Achsen angetrieben sind, fällt der Term Achsenangetrieben/Achsenalle weg. Wenn nicht alle Achsen der Lokomotive angetrieben sind, gilt die Formel nur dann, wenn jede Achse ungefähr die gleiche Last aufnimmt.
Zugkraftgleichung
Die benötigte Zugkraft kann mit der folgenden Formel, der sogenannten Zugkraftgleichung, berechnet werden:
$$F_Z=(m_{Lok}+m_{Wagen})·g·(w_R+w_L+w_S+w_K+w_B)$$
| FZ: | Erforderliche Zugkraft in N |
| mLok: | Masse der Lok in kg |
| mWagen: | Gesamtmasse aller angehängten Wagen in kg |
| g: | Erdbeschleunigung in m/s² |
| wR: | Rollwiderstand |
| wL: | Luftwiderstand |
| wS: | Steigungswiderstand |
| wK: | Krümmungswiderstand |
| wB: | Beschleunigungswiderstand |
Wie man die einzelnen Widerstände berechnet, wird auf einer eigenen Unterseite beschrieben:
Berechnung der erforderlichen Leistung
Die erforderliche Leistung am Rad errechnet sich zu
$$P=F_Z·v$$
| P: | Erforderliche Leistung in W |
| FZ: | Vorhandene Zugkraft in N |
| v: | Geschwindigkeit in m/s |
Die gesamte Antriebsleistung des Fahrzeuges muss natürlich noch höher sein, da Verluste des Antriebsstrangs (zum Beispiel Getriebe) und des Motors zu berücksichtigen sind!
Erreichbare Geschwindigkeit
Um bei gegebener Leistung die erreichbare Geschwindigkeit berechnen zu können, muss man die Gleichung für die erforderliche Leistung umformen. Das Problem dabei ist, dass die Geschwindigkeit zum Quadrat in der Berechnung des Luftwiderstandes enthalten ist. Man kann jedoch die entstehende Gleichung in folgende Form bringen:
$$v^3+a · v^2+b · v+c=0$$
Nun ist es möglich, die Geschwindigkeit v mit den Cardanischen Formeln zu berechnen.
Werbung
Seite erstellt 2013/2014. Zuletzt geändert am: