Unter Iteration versteht man das öftere Wiederholen von gleichen oder ähnlichen Handlungen mit dem Ziel, letztlich eine genügend genaue Lösung zu bekommen, also eine Näherung. Manchmal ist es sogar möglich, die exakte Lösung zu berechnen.
Hier wird zum besseren Verständnis anhand eines Beispiels demonstriert, wie man die Lösung einer einfachen Gleichung mithilfe der Iteration finden kann. Das zweite Beispiel zeigt, dass die Iteration für die Verwendung vieler meiner Rechner unter Umständen sehr nützlich ist.
Werbung
Beispiel I: einfache Gleichung
Die folgende einfache lineare Gleichung ist gegeben:
$$2x + 3 = 13$$
Man kann diese Gleichung natürlich durch einfaches Umformen (= Umstellen) lösen:
2x + 3 = 13 / -3
2x = 13 – 3
2x = 10 / ÷5
x = 5
Lösung dieser Gleichung durch Iteration
Alternativ findet man die Lösung auch mittels Iteration:
- Zunächst nimmt man zum Beispiel x = 10 an. Einsetzen in die Gleichung liefert: 2*10 + 3 = 23. Das Ergebnis ist viel größer als 13.
- 2. Durchführung des Versuchs mit einer kleineren Zahl: x = 6. Man erhält: 2*6 + 3 = 15. Schon viel besser!
- 3. Versuch: x = 4. Man erhält: 2*4 + 3 = 11. Das Ergebnis ist etwas zu klein.
- 4. Versuch: x = 5. Man erhält: 2*5 + 3 = 13. Dieses Ergebnis stimmt mit der rechten Seite der ursprünglichen Gleichung überein, somit handelt es sich bei x = 5 sogar um die exakte Lösung.
Normalerweise wird kein vernünftiger Mensch so eine einfache Gleichung auf diese Art lösen. Das Beispiel zeigt jedoch sehr anschaulich, was man unter Iteration versteht.
Beispiel II: Berechnung der Kraft F mit Balkenrechner
Viele meiner Rechner können zum Beispiel die Kraft F nicht berechnen, da sie bekannt sein muss. Es gibt jedoch die Möglichkeit, die gesuchte Kraft mittels Iteration zu bestimmen. Dies wird anhand des Balkenrechners gezeigt.
Angabe
Ein 2450 mm langes Aluminium-Vierkantrohr wird auf einem Festlager und einem Loslager gelagert und hat die folgenden Maße:
Höhe 40 mm, Breite 180 mm, alle Wandstärken 4 mm.
Es ist die nötige Kraft F in Balkenmitte zu berechnen, um eine Durchbiegung von 7 mm zu erreichen.
Berechnung von F mittels Balkenrechner & Iteration
Prinzipiell kann mein Balkenrechner nur die Durchbiegung bei gegebener Kraft F berechnen, in diesem Beispiel ist aber die Kraft gesucht und die Durchbiegung gegeben. Dennoch kann diese Aufgabe indirekt mit dem Balkenrechner gelöst werden, indem man die Methode der Iteration verwendet:
- Dazu werden zunächst alle bekannten Daten – also die Länge und die Abmessungen des Balkens, der Abstand a der Kraft, der Werkstoff und so weiter – in den Rechner eingetragen. Anschließend verändert man die Kraft F so lange, bis man ein möglichst genaues Ergebnis bekommt.
- Als Erstes führt man z. B. mit der voreingestellten Kraft F = 8,5 kN eine Berechnung durch. Man erhält für die Durchbiegung fm = 75,87 mm, was jedoch viel größer als die gewünschte Durchbiegung von 7 mm ist.
- Für den 2. Versuch wählt man daher einen wesentlich kleineren Wert für die Kraft, also zum Beipiel F = 0,5 kN. Man erhält: fm = 4,46 mm, was etwas zu klein ist.
- Da der beim vorigen Versuch ermittelte Wert zu klein war, wählt man nun eine etwas größere Kraft: F = 0,8 kN –> fm = 7,14 mm. Dieses Ergebnis ist schon ganz gut und nur mehr etwas zu groß.
- 4. Versuch: F = 0,7 kN –> fm = 6,25 mm (ganz gut, etwas zu klein)
- 5. Versuch: F = 0,75 kN –> fm = 6,69 mm (besser, noch immer etwas zu klein)
- Nach weiteren Versuchen erhält man das exakte Ergebnis: F = 0,784 kN. Die Durchbiegung fm entspricht nun genau den gewünschten 7 mm.
Wie die Felder des Rechners auszufüllen sind, zeigen die folgenden beiden Screenshots, wobei die Kraft F natürlich bei jedem Versuch geändert werden muss:
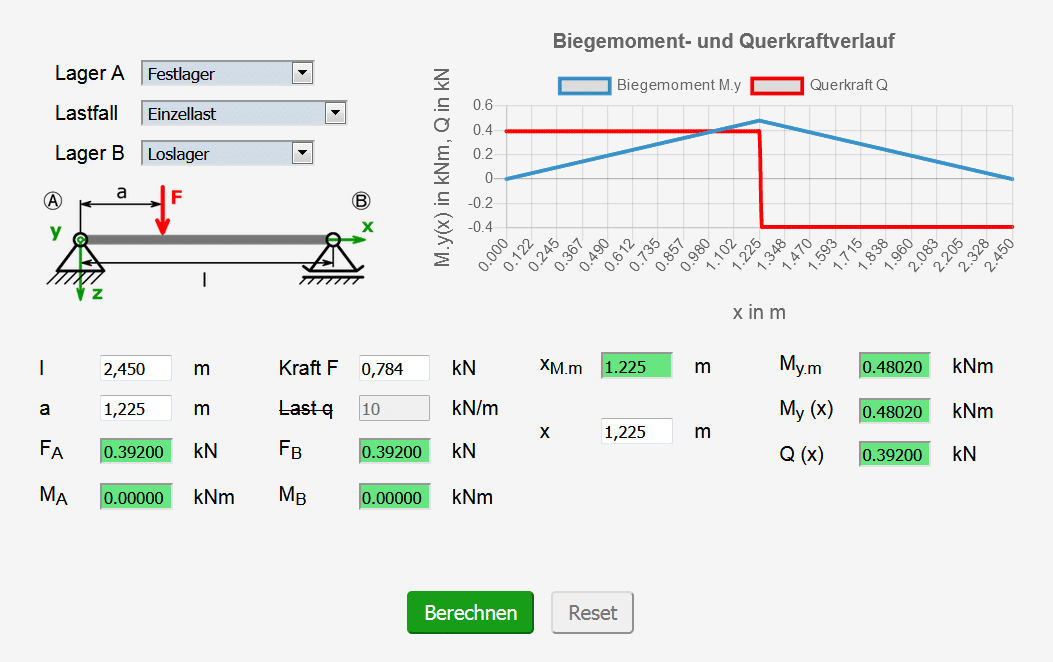
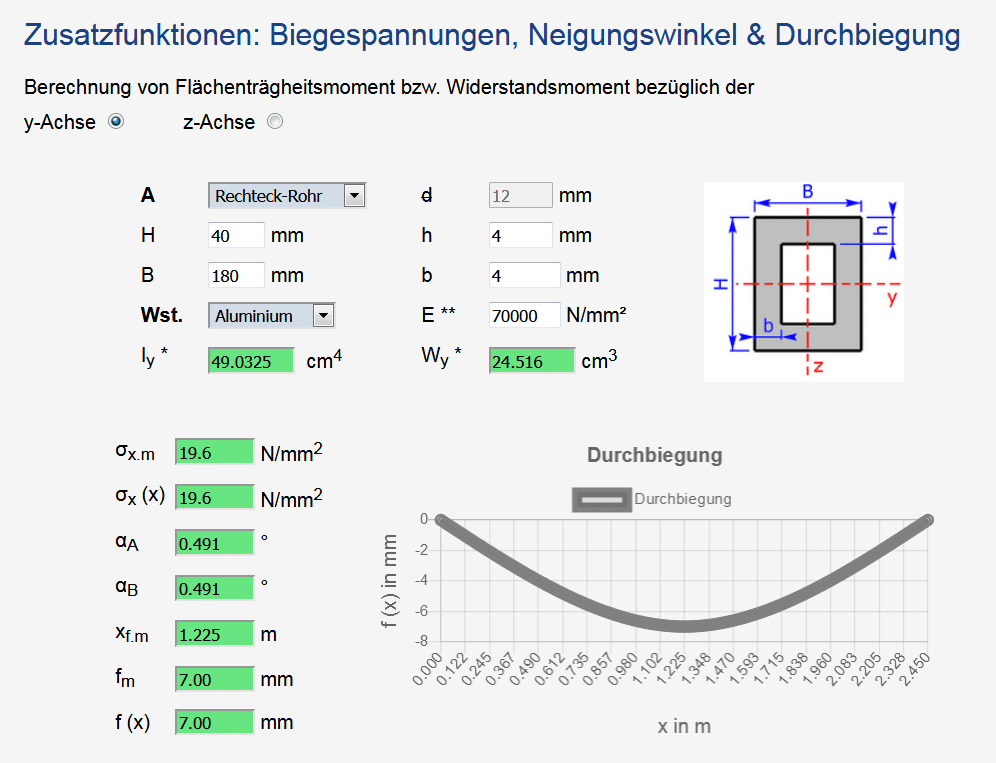
Werbung
Seite erstellt am 27.04.2020. Zuletzt geändert am 09.11.2021.