Dieser Online-Rechner berechnet den Umfang und den Flächeninhalt verschiedener ebener Figuren:
- Dreiecke: allgemein, rechtwinkelig, gleichschenkelig, gleichseitig
- Vierecke: Rechteck, Quadrat, Parallelogramm, Rhombus (Raute), Deltoid, Trapez
- Regelmäßiges Sechseck und Achteck (Oktagon)
- Kreisteil, Kreis, Kreisring und Ellipse
Weiters können von einigen Figuren der Inkreis- und der Umkreisradius sowie die Länge der Diagonalen ermittelt werden. Nach dem Rechner finden Sie Informationen zu den beim Rechner auswählbaren Figuren.
Werbung
Rechner für Umfang & Flächeninhalt
Mit der Voreinstellung können Sie den Flächeninhalt, den Umfang, den Umkreisradius und die Länge der Diagonalen für ein Rechteck berechnen.
Hinweise für die Verwendung des Rechners
- Etwas weiter unten findet man Skizzen von allen zur Auswahl stehenden Figuren.
- Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular!
Begriffsklärung & Skizzen der verfügbaren Figuren
Welche Dreiecke und Vierecke gibt es? Was ist eine Ellipse? Was versteht man unter einem Umfang?
Umfang
Als Umfang wird die Summe jener Linien bezeichnet, die die ebenen Figuren begrenzen.
Beispiel Dreieck:
Der Umfang eines Dreiecks ist daher die Summe der Längen aller drei Seiten:
$$U = a + b + c$$
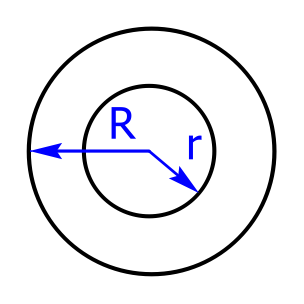
Beispiel Kreisring:
Zur Berechnung des Umfangs eines Kreisrings müssen der Umfang des äußeren Kreises und der Umfang des inneren Kreises addiert werden:
$$U = 2·R·π + 2·r·π = 2·π·(R + r)$$
Dreiecke
Man unterscheidet vier verschiedene Arten von Dreiecken:
- allgemeine Dreiecke
- rechtwinkelige Dreiecke
- gleichschenkelige Dreiecke
- gleichseitige Dreiecke
Die Winkelsumme von Dreiecken beträgt stets 180°. Alle Dreiecke haben sowohl einen Inkreis als auch einen Umkreis.
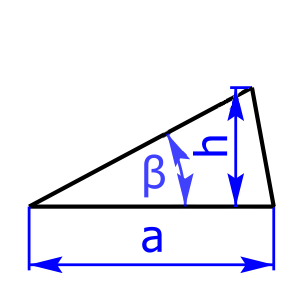
Bei rechtwinkeligen Dreiecken hat einer der drei Winkel 90° (= rechter Winkel, in der Skizze der Winkel zwischen den Seiten a und b). Die Seite gegenüber dem rechten Winkel heißt Hypotenuse und ist die längste der drei Seiten. Die beiden anderen Seiten heißen Katheten. Im rechtwinkeligen Dreieck gilt der Satz des Pythagoras:
$$a^2 + b^2 = c^2$$
Sind also in einem rechtwinkeligen Dreieck zwei Seiten bekannt, kann die dritte Seite durch Umformen (= Umstellen) berechnet werden.

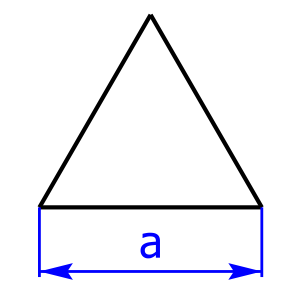
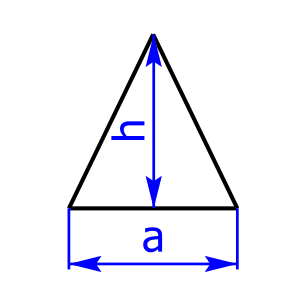
Gleichseitige Dreiecke haben drei gleich lange Seiten, drei gleich lange Höhen und zudem sind die Winkel alle gleich groß, nämlich 180°/3 = 60°.
Gleichschenkelige Dreiecke sind um eine der Höhen symmetrisch. Die beiden anderen Höhen, zwei Seiten und zwei Winkel sind gleich groß.
Vierecke
Man unterscheidet sechs Vierecke, wobei die Winkelsumme immer 360° beträgt:
- Rechteck und Quadrat
- Parallelogramm und Rhombus (Raute)
- Deltoid und Trapez
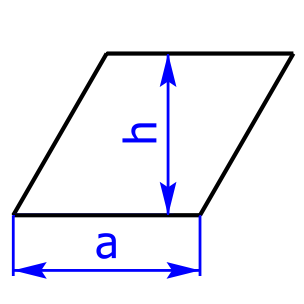
Bei einem Parallelogramm sind stets zwei gegenüberliegende Seiten gleich lang und parallel. Zudem sind die beiden gegenüberliegende Winkel jeweils gleich groß. Parallelogramme haben weder einen Inkreis noch einen Umkreis.

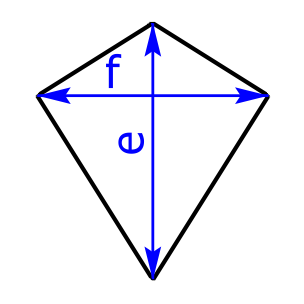
Ein spezielles Parallelogramm ist die Raute oder auch Rhombus genannt, bei dem zusätzlich noch alle vier Seiten gleich lang sind. Rauten besitzen einen Inkreis, aber keinen Umkreis. Die beiden Diagonalen e und f stehen aufeinander normal und sind zugleich die Symmetrieachsen.
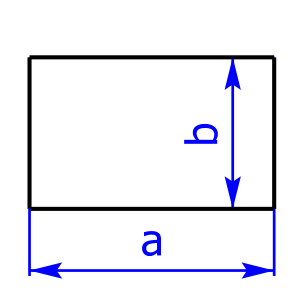
Eine Spezialform des Parallelogramms ist das Rechteck. Auch hier haben die gegenüberliegenden Seiten die gleiche Länge, zudem sind noch alle vier Winkel rechte Winkel und die beiden Diagonalen besitzen dieselbe Länge. Rechtecke sind symmetrisch um zwei Achsen.
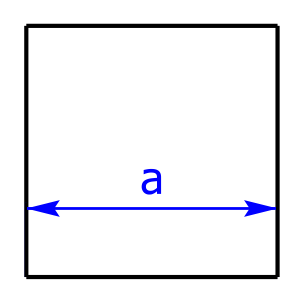
Das Quadrat ist eine spezielle Raute bzw. ein spezielles Rechteck: Die vier Seiten sind gleich lang, parallel und bei allen Winkeln handelt es sich zudem um rechte Winkel. Quadrate haben vier Symmetrieachsen.
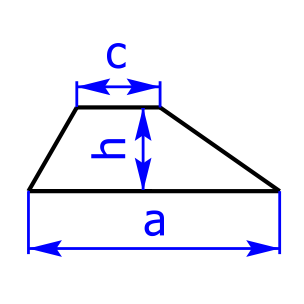
Weitere Vierecke sind das Deltoid und das Trapez:
Kreis und Ellipse
Der Kreis ist ein Spezialfall der Ellipse, bei der die beiden Brennpunkte zusammenfallen: Dieser Punkt wird Mittelpunkt M genannt. Ellipsen besitzen zwei Symmetrieachsen, Kreise haben hingegen unendlich viele Symmetrieachsen, die stets durch den Mittelpunkt M verlaufen.
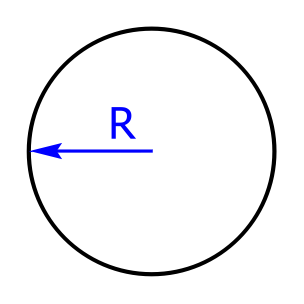

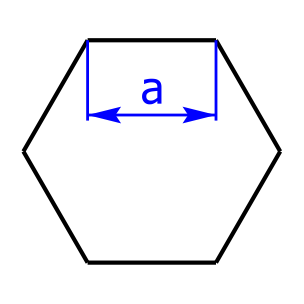
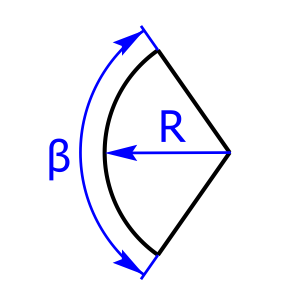
Skizzen von Sechseck, Achteck, Kreisring und Kreisteil

Werbung
Seite erstellt im Mai 2020. Zuletzt geändert am 03.11.2021.