This page in English: Calculator for beams
Balkenrechner für Biegemoment, Biegespannung, Querkraft & Auflagerreaktionen eines Trägers
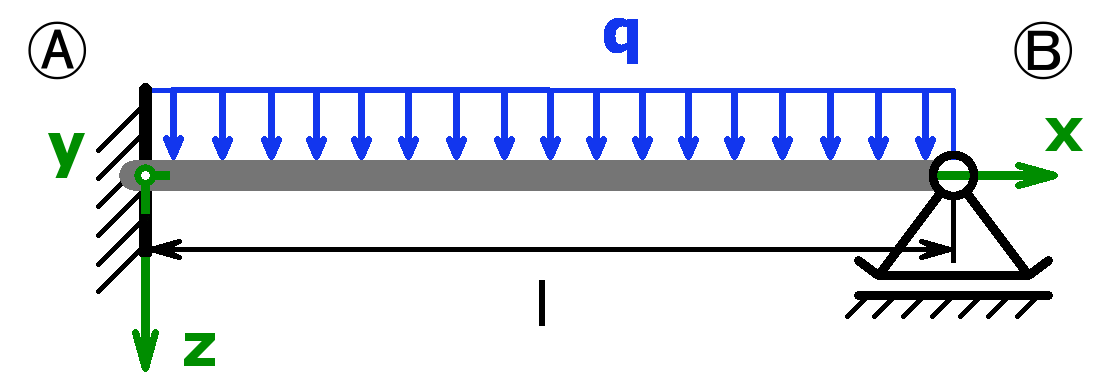
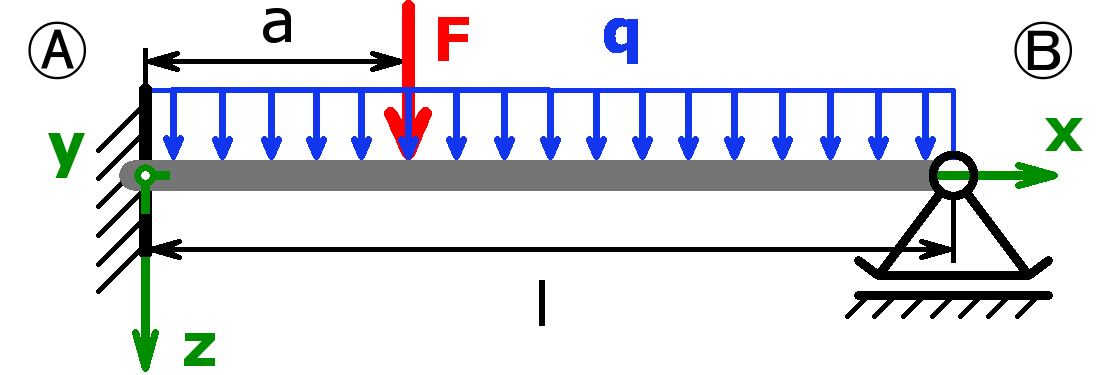
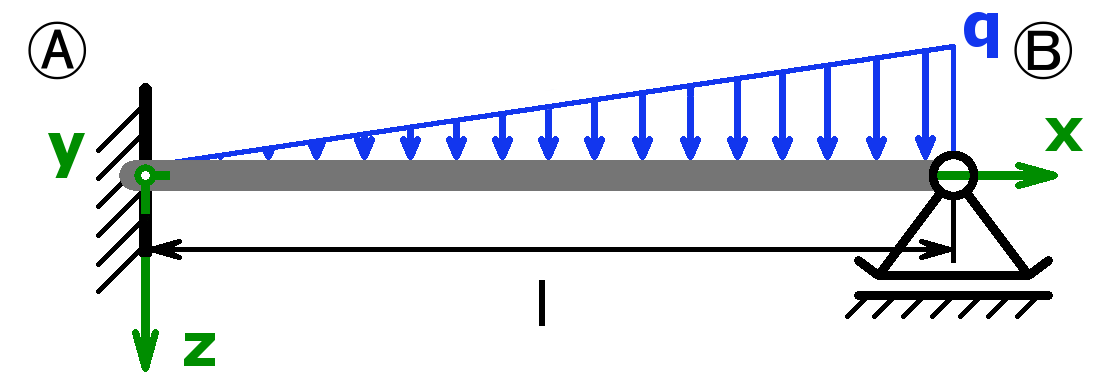
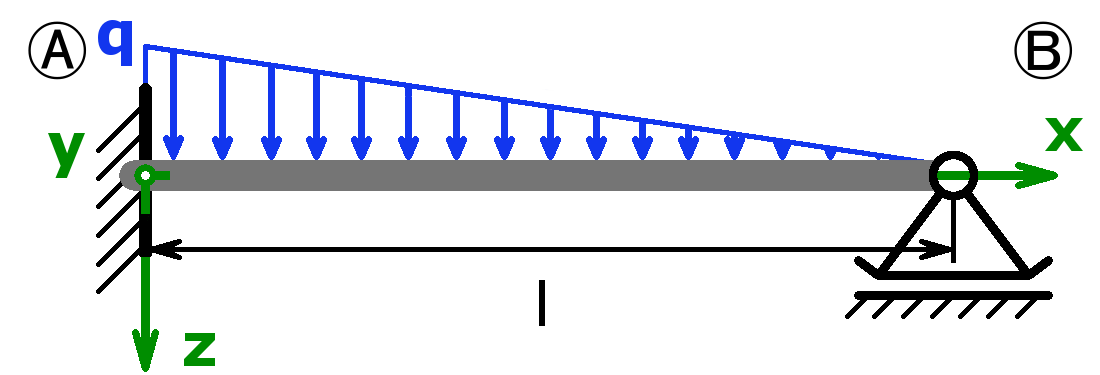
Dieser Online-Balkenrechner berechnet die in den beiden Auflagern wirkenden Kräfte bzw. Momente (=Auflagerreaktionen) und die Neigungswinkel statisch bestimmter und statisch unbestimmter Träger (bzw. Balken) auf zwei Stützen, auch als Einfeldträger bezeichnet. Als Belastung kann eine Gleichlast oder eine Einzellast bzw. die Kombination aus beiden oder eine Dreieckslast gewählt werden.
Zudem können die Querkraft, das Biegemoment, die Biegespannung und die Durchbiegung an einer gewünschten Stelle x und auch die Maximalwerte inklusive der dazugehörenden Stelle bestimmt werden. Der Verlauf des Biegemoments, der Querkraft und der Durchbiegung in Abhängigkeit der Länge x wird in zwei Diagrammen grafisch dargestellt. Die zulässigen Biegespannungen für ausgewählte Werkstoffe finden Sie in einer Tabelle weiter unten auf dieser Seite.
Werbung
Rechner für Auflagerreaktionen, Querkraft & Biegemoment von statisch (un)bestimmt gelagerten Balken
* Um diese Werte eingeben zu können, wählt man unter Querschnitt A --> Sonstige Profile --> "Eigenes Profil".
** Der E-Modul wird automatisch durch die Auswahl eines Werkstoffs eingetragen, kann jederzeit geändert werden; passende Werte gibt es zum Beispiel auf Wikipedia.
Achtung:
Bei Profilen mit Loch werden unter den Zusatzfunktionen nur I, W und die maximale Spannung korrekt berechnet. Wählen Sie für die anderen Werte ein Profil ohne Loch!
Links zu weiteren Unterseiten
- Lagerreaktionen berechnen (statisch bestimmte Träger); Satz von Castigliano / Menabrea
- Formeln, die dieser Rechner verwendet (Berechnung der Auflagerreaktionen, Winkel & Durchbiegung)
- Tipps: Ist zum Beispiel die Kraft F oder die Länge l (= Spannweite des Balkens) gesucht, kann man die Lösung per Iteration ermitteln. Für weitere Lastfälle sei auf die Seite Superpositionsprinzip verwiesen.
Wichtige Hinweise
- Die Schubspannung wird nicht berücksichtigt. Sie kann jedoch normalerweise vernachlässigt werden. Bei sehr kurzen Trägern ist das aber nicht zulässig!
- Die Einheit der Belastungen ist stets in kN einzugeben, also muss man gegebenenfalls die Einheiten umrechnen: 1 kN = 1000 N; in der Regel gilt auf der Erde: 1 kg ≈ 9.81 N = 0.00981 kN. Beträgt die Last zum Beispiel 250 kg, setzt man in den Rechner für die Kraft F = 2.45 kN ein: 250*9.81/1000 = 2.45 kN.
- Die Berechnung der Flächenträgheitsmomente und der Widerstandsmomente erfolgt für idealisierte Profile, das heißt, schräge Kanten und Abrundungen werden nicht berücksichtigt!
- Die Werte für die zulässigen Biegespannungen nach Bach finden Sie etwas weiter unten auf dieser Seite.
- Die grafische Darstellung der Durchbiegung und die Berechnung haben entgegengesetzte Vorzeichen. Das Vorzeichen, das sich durch die Berechnung ergibt, ist korrekt (positive z-Achse weist nach unten). Es ist jedoch anschaulicher, wenn die Durchbiegung so dargestellt wird, wie sich der Balken tatsächlich verformt.
- Für die richtige Funktion wird keine Gewähr übernommen - für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular!
Erklärung der Abkürzungen
Fliegende L. ist die Abkürzung für fliegende Lagerung; die Kraft F greift außerhalb der beiden Lager an.
| FA | Auflagerkraft im Lager A in z-Richtung; in x-Richtung wirken keine Kräfte! |
| FB | Auflagerkraft im Lager B in z-Richtung; in x-Richtung wirken keine Kräfte! |
| MA | Einspannmoment im Lager A |
| MB | Einspannmoment im Lager B; bei fliegender Lagerung Moment im Balken bei x = a. |
| xM.m |
Stelle des maximalen Biegemoments; Achtung: es wird auch bei mehreren, gleich großen Biegemomenten nur eine Stelle angegeben! |
| My.m | maximales Biegemoment |
| x |
beliebige Stelle, an der das Biegemoment, die Querkraft, die Biegespannung und die Durchbiegung berechnet werden soll |
| My (x) | Biegemoment an der Stelle x |
| Q (x) | Querkraft an der Stelle x |
| A | Querschnitt des Profils |
| Wst. | Werkstoff ("Material") |
| E-M | E-Modul, passende Werte gibt es zum Beispiel auf Wikipedia |
| Iy | Flächenträgheitsmoment |
| Wy | Widerstandsmoment |
| σx | Biegespannung in der Randfaser an der Stelle x |
| σx.m |
maximale Biegespannung im Balken an der Stelle xM.m. Es ist zu prüfen, ob der Balken diese Spannung auch aushält! |
| αA | Neigungwinkel (= Verdrehung) des Balkens im Lager A |
| αB | Neigungwinkel (= Verdrehung) des Balkens im Lager B |
| xf.m | Stelle der maximalen Durchbiegung des Trägers |
| fm |
maximale Durchbiegung des Balkens an der Stelle xf.m unter der Last F. Es ist eventuell zu prüfen, ob diese Durchbiegung auch zulässig ist! In der Regel reicht es jedoch, wenn nur die Spannungen kontrolliert werden. |
| f (x) | Durchbiegung (= Verschiebung) des Balkens an der Stelle x |
Weitere Hinweise für die Verwendung des Rechners
Damit die Spannungen, Winkel und Durchbiegungen korrekt berechnet werden können, ist auf die Einbaulage des Balkens zu achten:
Mit der Voreinstellung "Berechnung von Flächenträgheitsmoment und Widerstandsmoment bezüglich der y-Achse" muss die Wirkungslinie der Kraft F genau in der z-Achse verlaufen (Ausnahme: U-Profil).
Bei der Auswahl "Berechnung von Flächenträgheitsmoment und Widerstandsmoment bezüglich der z-Achse" muss die Wirkungslinie der Kraft F hingegen genau in der y-Achse verlaufen (Ausnahme: T-Profil), das heißt, der Träger wird um 90° gedreht.
- Weist die Kraft F bzw. q in die andere Richtung, setzt man vor diese Belastung(en) ein negatives Vorzeichen.
- Die Auflager können als Festlager, Loslager, feste Einspannung (auch beidseitig) oder als freies Ende ausgeführt sein.
- Folgende Querschnitte sind verfügbar, wobei die mit * bezeichneten Profile auch ein Durchgangsloch bzw. eine Bohrung besitzen können:
-
- Rundstange (Kreis) *
- Rundrohr (Kreisring)
- Halb-Rundstab (Halbkreis)
- Rechteck-Profil *
- Rechteck-Hohlprofil / Formrohr / Vierkantrohr *
- Rechteck mit Bohrung
- I- bzw. H-Profil (Doppel-T-Träger) *
-
- U- bzw. C-Profil *
- T-Profil
- L-Profil (Winkelprofil), gleich- und ungleichschenkelig
- L-Profil (gleichschenkelig) um 45° gedreht
- Gleichschenkeliges / gleichseitiges Dreieck
- Sechseck / Sechskant
- Achteck / Achtkant
- Achtung: Bei senkrecht belasteten U-Trägern können die Spannungen und Durchbiegungen nur dann richtig berechnet werden, wenn
-
- die Kraft F im Schubmittelpunkt angreift
- oder zwei U-Träger miteinander verbunden werden, also [ ] bzw. ] [ und die Belastung in der Mitte der beiden Balken erfolgt. In diesem Fall ist die halbe Kraft F in den Rechner einzusetzen.
- Eventuelle Sprünge im Querkraftverlauf können nicht ganz korrekt dargestellt werden.
Werbung
Zulässige Biegespannungen nach Bach
Normalerweise ist die maximal auftretende Spannung das Auslegungskriterium für Bauteile. In einigen Fällen ist jedoch auch die maximale Durchbiegung zu beachten, zum Beispiel bei der Lagerung von Wellen. In der folgenden Tabelle findet man die zulässigen Biegespannungen nach Bach. Die Auswahl der korrekten Werte erfolgt zunächst aufgrund des Werkstoffs und der Art der Belastung, also ruhend, schwellend oder schwingend (= wechselnd).
Wird die Streckgrenze Re bzw. die Fließgrenze ReN überschritten, kommt es zu plastischen - also bleibenden - Verformungen des Bauteils, was im Maschinenbau in aller Regel auszuschließen ist. Bei der Zugfestigkeit Rm handelt es sich um die maximale Spannung, die ein Werkstoff aushält. Wird diese Spannung überschritten, kommt es zum Bruch des Balkens.
Welcher Wert im jeweiligen Bereich zu wählen ist, hängt unter anderem ab von der
- Größe des Bauteils
- Kerbwirkung, z. B. Nuten, Absätze, Löcher, ...
- Beschaffenheit der Oberfläche
- Auslegung auf Zeitfestigkeit oder auf Dauerfestigkeit
Die Werkstoffkennwerte für ein paar bekannte Stähle finden Sie in dieser Tabelle, wobei die zulässigen Spannungen immer Sicherheiten beinhalten:
| Zulässige Biegespannungen in N/mm² | ||||
|
Beanspruchung |
S235 (St 37) * |
S355 (St 52) ** |
42CrMo4 * |
Nadelholz |
| ruhend (= statisch) | 110 - 165 (- 280)1 | 155 - 235 (- 390)1 | 385 - 660 (- 990)1 | 10 *** |
| schwellend | 70 - 105 (- 270)2 | 100 - 150 (- 380)2 | 245 - 420 (- 825)2 | |
| schwingend | 50 - 75 (- 180)2 | 70 - 105 (- 255)2 | 175 - 240 (- 550)2 | |
| Streckgrenze Re 3 | 235 | 355 | 900 | |
| Zugfestigkeit Rm 3 | 360 | 510 | 1100 | ~ 30 |
* Werte nach Bach aus "Grundlagen der Maschinenelemente" (Arbeitsblätter zum Skriptum), TU Wien
** berechnet aus den Werten für S235
*** Wert für Konstruktionsholz nach: https://www.bullinger.de/produkte/konstruktionsholz/statikbauphysik.html
1 Die Werte in Klammern entsprechen der Streckgrenze Re; ansonsten gilt ähnliches wie unter 2.
2 Die Werte in den Klammern gelten für einen idealen, sehr glatten Probestab mit einem Durchmesser von 16 mm (Sicherheit = 1) und sind dem Tabellenbuch Roloff/Matek, Maschinenelementeo entnommen. Diese Werte können in der Praxis eigentlich nie verwendet werden und stehen daher in einer Klammer, weil man immer gewisse Sicherheiten einplanen muss.
3 Mindestwerte, gelten für einen Durchmesser von 16 mm
Formeln & auswählbare Kombinationen
Formeln
Die vom Rechner verwendeten Formeln findet man auf dieser Unterseite:
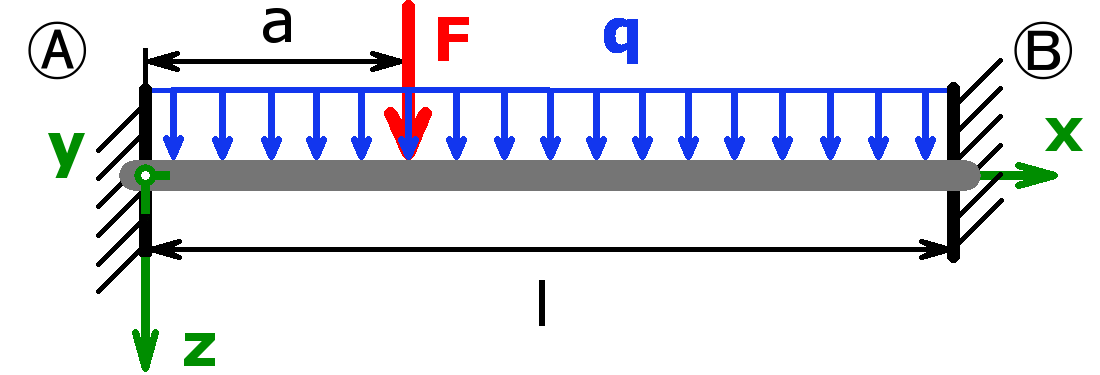
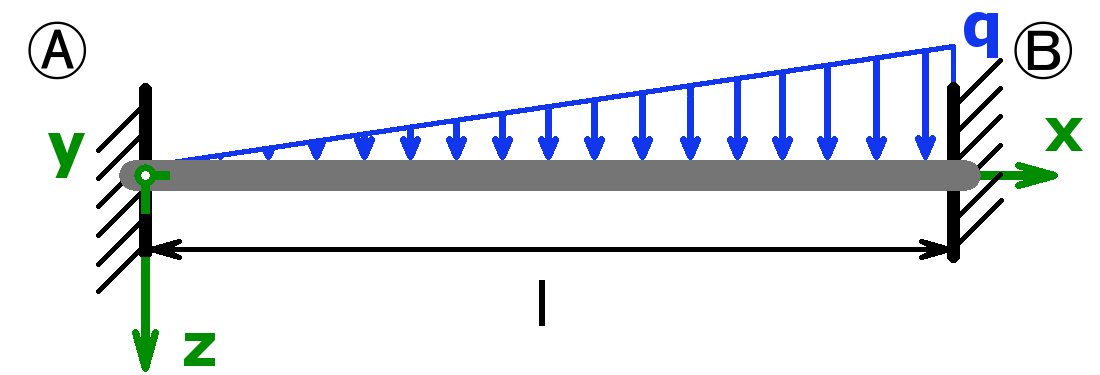
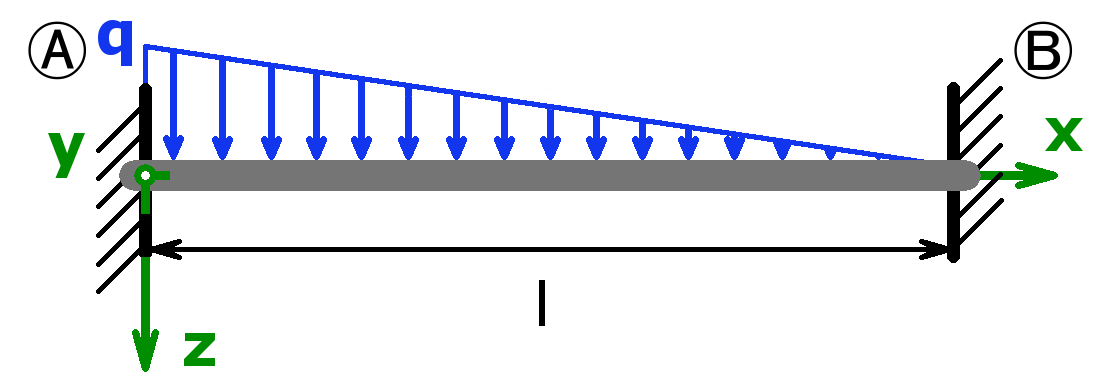
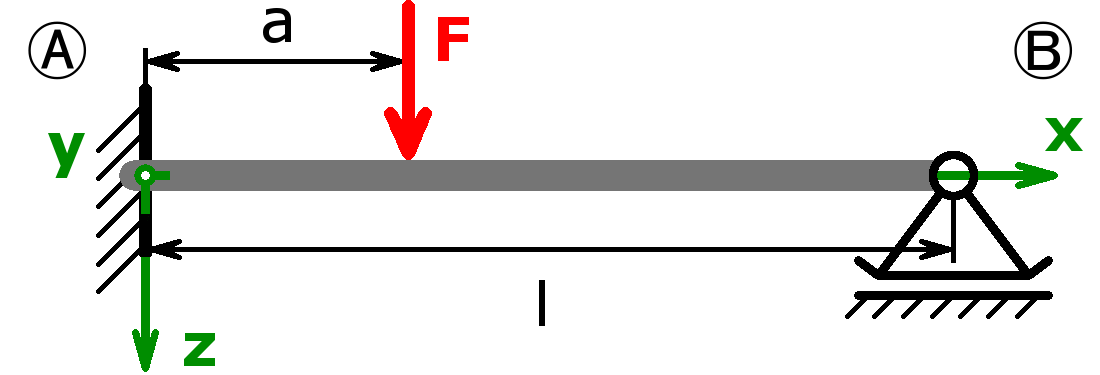
Mit dem Rechner können die Auflagerkräfte sowohl statisch bestimmter als auch statisch unbestimmter Systeme berechnet werden. Lager A kann als Festlager oder als feste Einspannung ausgeführt sein. Lager B darf ein Loslager, eine feste Einspannung oder ein freies Ende sein. Handelt es sich bei Lager A um eine feste Einspannung und ist Lager B gar nicht vorhanden (= freies Ende), nennt man diesen Aufbau Kragträger, Kragbalken oder auch Kragarm.
Greift die Kraft außerhalb der Lager an, handelt es sich um eine sogenannte fliegende Lagerung. Diese Lagerungsart kommt öfters bei Wellen bzw. Achsen vor.
Folgende Kombinationen sind möglich:
Statisch bestimmt
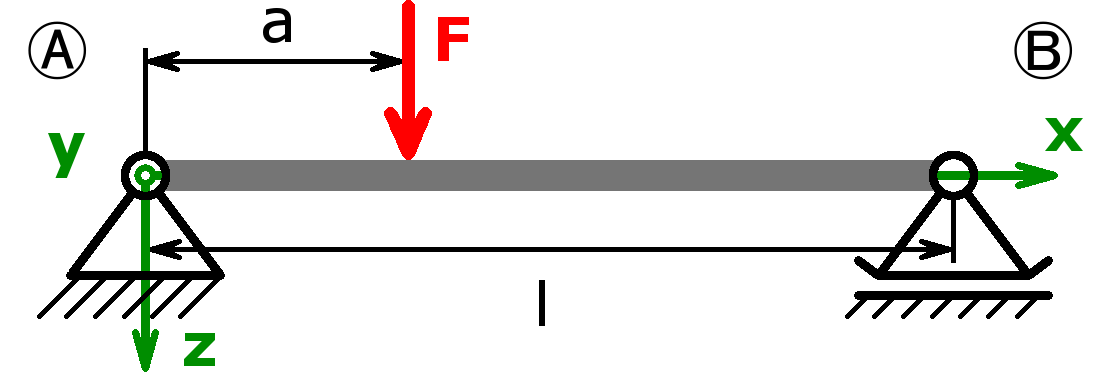
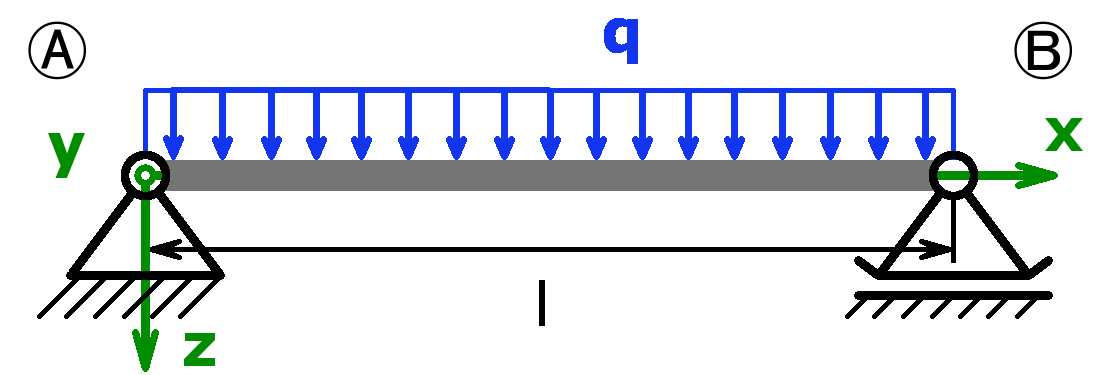
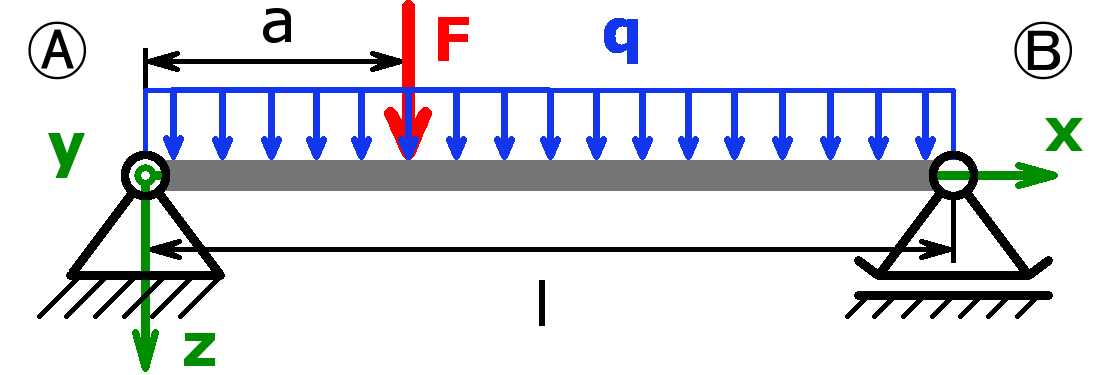
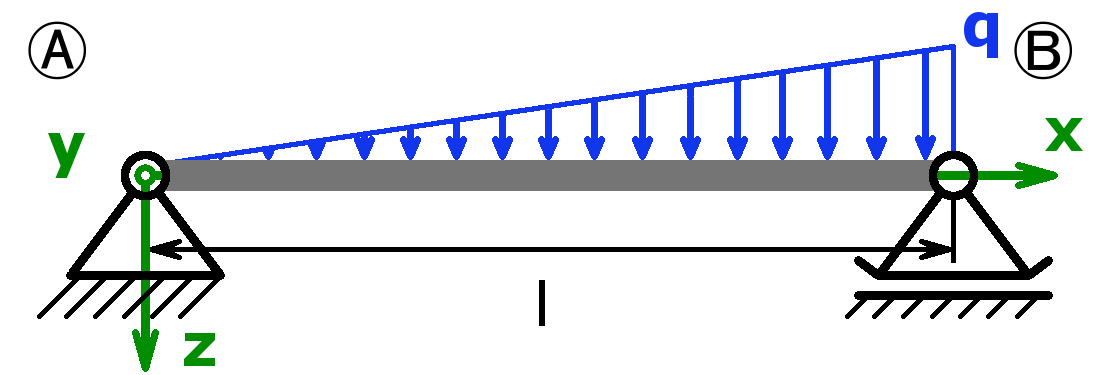
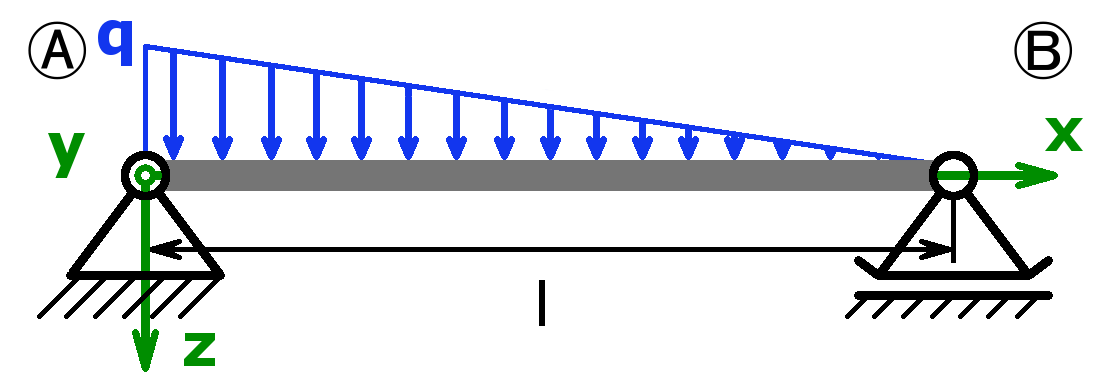
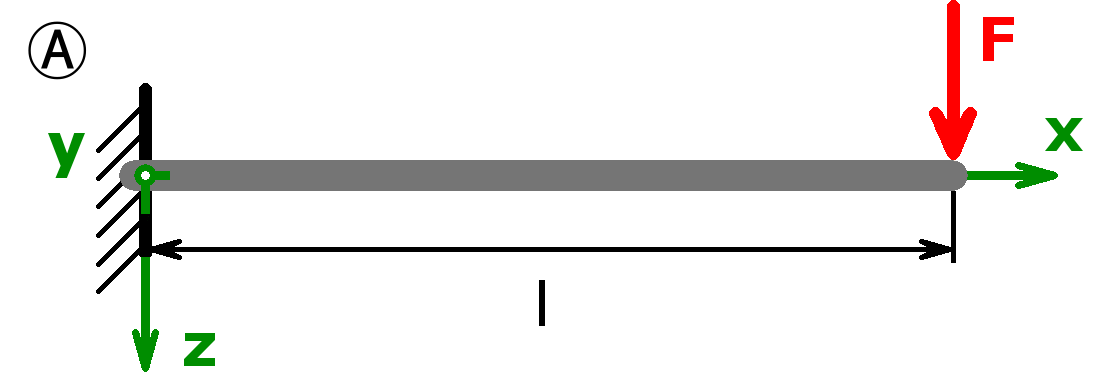
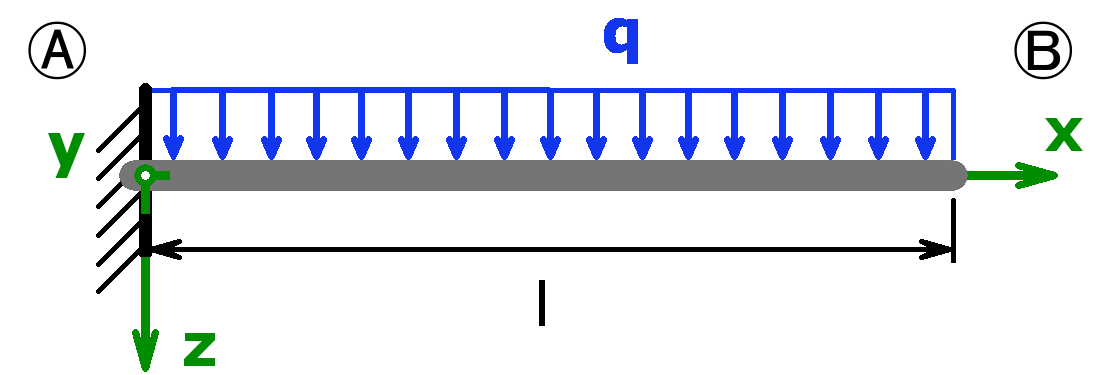
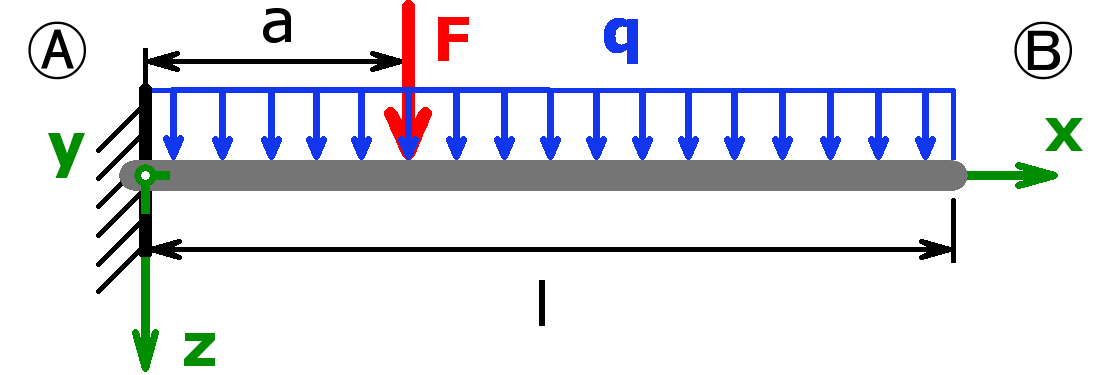
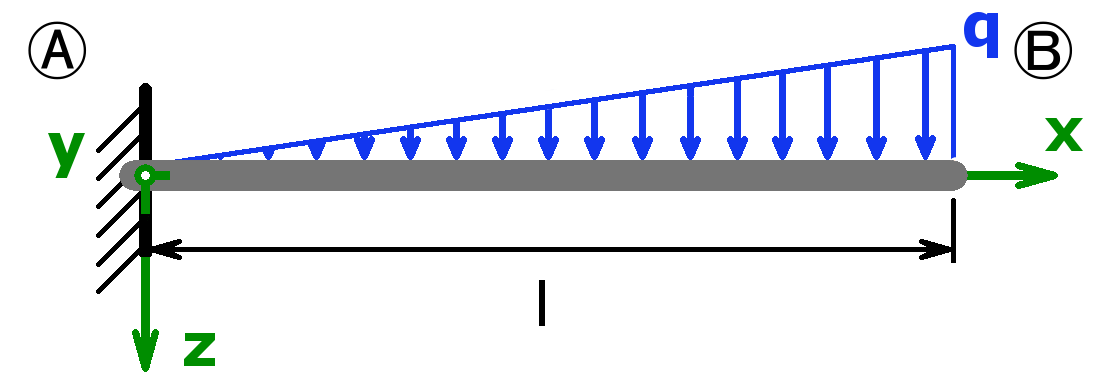
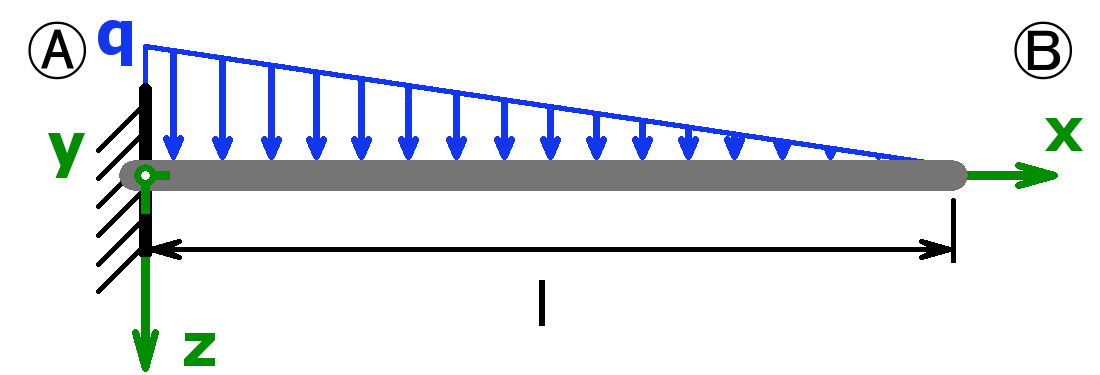
Statisch unbestimmt
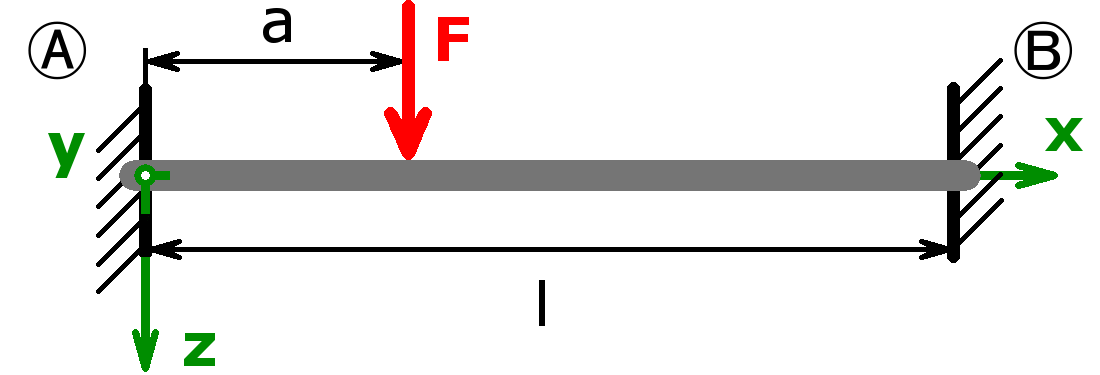
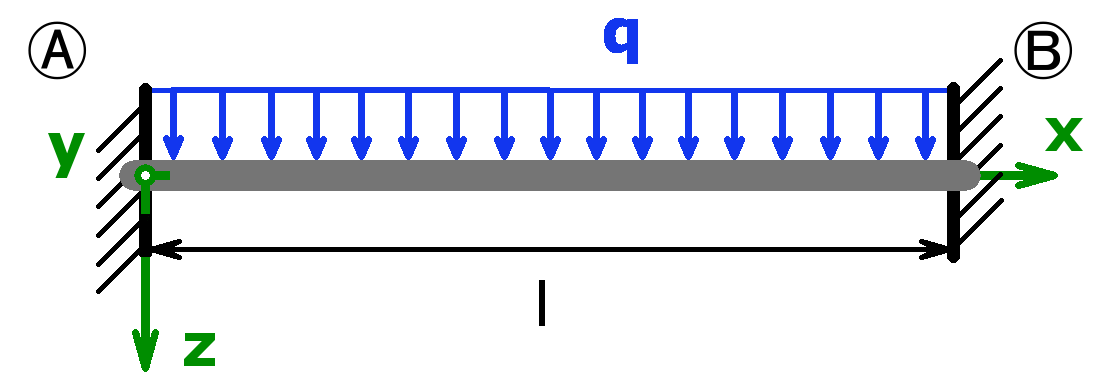
Werbung
Seite erstellt im November 2017. Zuletzt geändert am 05.01.2021.