Superpositionsprinzip (Überlagerungsprinzip)
Mit Superposition ist hier die Überlagerung von Belastungen gemeint. Manchmal sind die Lösungen einzelner Lastfälle bekannt, zum Beispiel aus Formelsammlungen oder auch vom Balkenrechner. In diesen Fällen kann es zweckmäßig sein, die Auflagerreaktionen für jeden Lastfall getrennt zu ermitteln und zuletzt die so erhaltenen Kräfte, Momente oder Durchbiegungen zu addieren.
Mittels Superposition lassen sich aber auch die Auflagerreaktionen statisch unbestimmter Systeme bestimmen.
Das Superpositionsprinzip wird hier anhand dreier Beispiele gezeigt:
- Beispiel I: Balken mit Einzellast und Gleichlast (statisch bestimmt)
- Beispiel II: Balken mit Gleichlast (statisch unbestimmt)
- Beispiel III: Anwendung einer meiner Rechner
Beispiel I: statisch bestimmter Balken
Angabe
Gegeben ist ein statisch bestimmter Balken mit einer Gleichlast q und einer Einzelkraft F laut Abbildung. Berechnen Sie die Auflagerkräfte in den Lagern A und B allgemein mittels Superposition mit den bekannten Formeln aus einer Formelsammlung!
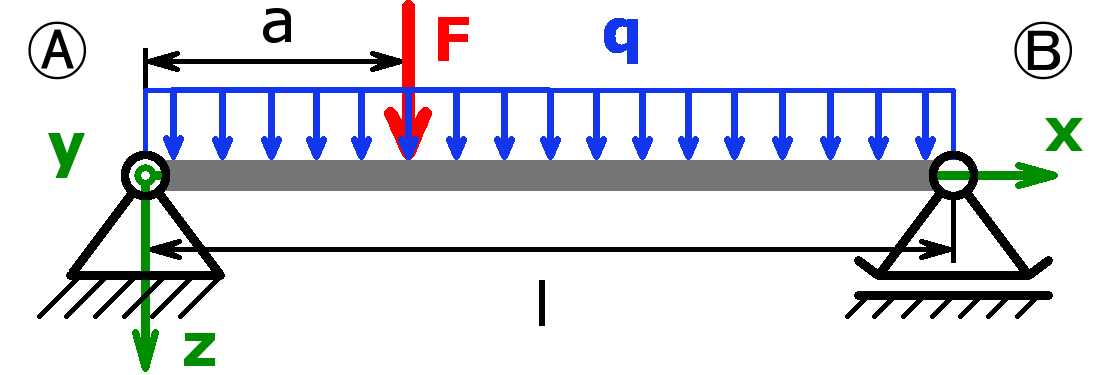
Lösung der Aufgabe mittels Superposition
Die Belastung des gegebenen Balkens setzt sich aus der Einzelkraft F und der Gleichlast q zusammen:
Für die Berechnung der Auflagerkräfte benötigt man zunächst die Formeln für die Einzelkraft F und für die Gleichlast q, die man zum Beispiel in meiner Formelsammlung für statisch bestimmte Systeme findet:
Auflagerkräfte zufolge Einzelkraft F
Auflagerkräfte zufolge Gleichlast q
Die gesamten Auflagerkräfte erhält man nun durch Addition der Auflagerkräfte aufgrund der Einzellast und zufolge der Gleichlast:
Beispiel II: 1-fach statisch unbestimmter Balken
Angabe
Gegeben ist ein statisch unbestimmter Balken mit einer Gleichlast q laut Abbildung. Berechnen Sie die Auflagerkräfte im Lager B allgemein mittels Superposition mit den bekannten Formeln aus einer Formelsammlung!
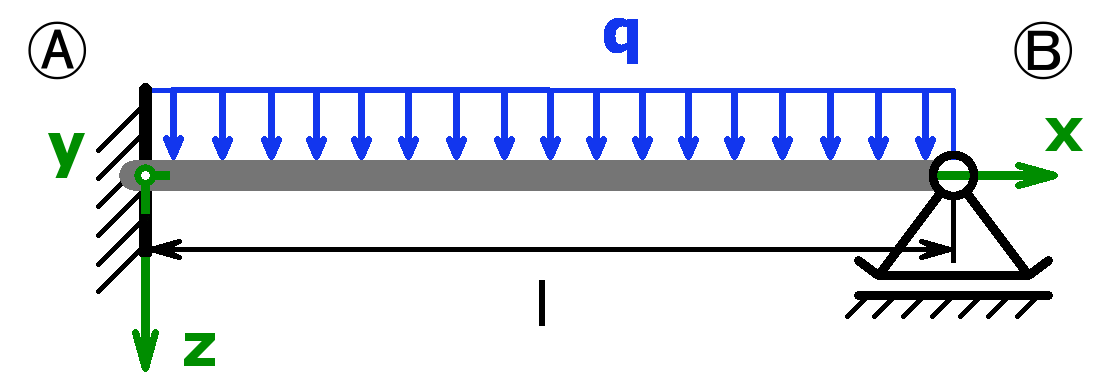
Lösung der Aufgabe mittels Superposition
Hinweis:
Dieses Beispiel wird auch mit dem Satz von Menabrea gelöst!
Man teilt das gegebene statisch unbestimmte System in zwei statisch bestimmte Systeme auf:
- fest eingespannter Balken unter Gleichlast
- fest eingespannter Balken mit Einzelkraft B, die der Auflagerkraft im Loslager B entspricht.
Nun gilt, dass die Durchbiegung zufolge der Gleichlast q und die Durchbiegung zufolge der Einzelkraft B gleich groß sein müssen. Die Formeln für die Durchbiegungen findet man zum Beispiel in meiner Formelsammlung:
Durchbiegung zufolge Gleichlast q
$$f_q=\frac{q⋅l^4}{8⋅E⋅I_y}$$
Durchbiegung zufolge Einzellast B
$$f_B=\frac{B⋅l^3}{3⋅E⋅I_y}$$
Gleichsetzen und vereinfachen ergibt:
$$f_q=f_B \Rightarrow \frac{q⋅l^4}{8⋅E⋅I_y}=\frac{B⋅l^3}{3⋅E⋅I_y}$$
$$ \Rightarrow \frac{q⋅l}{8}=\frac{B}{3}$$
Zuletzt multipliziert man diese Gleichung noch mit 3. Man erhält für die gesuchte Auflagerkraft B:
$$B=\frac {3⋅q⋅l}{8}$$
Beispiel III: Person steht auf Tisch mit vier Beinen
Angabe
Auf einem Tisch mit einer Eigenmasse von 20 kg steht eine Person, die 80 kg wiegt und im Bild mit F markiert ist. Die mit A, B, C und D beschrifteten Punkte stellen die vier Auflager dar und symbolisieren die Tischbeine (Draufsicht). Der Koordinatenursprung befindet sich genau in der Mitte des Rechtecks.
Wie groß sind die Belastungen in den vier Aufstandspunkten, wenn für die Abstände folgende Zahlenwerte gelten: a = 1 m, b = 8 dm, x = 20 cm und y = 100 mm.
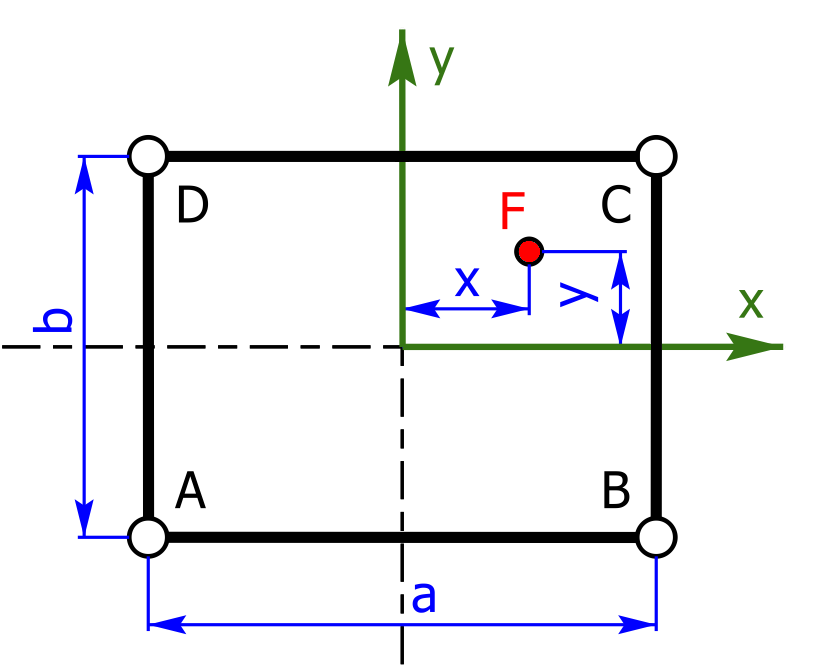
Wichtiger Hinweis:
Stützt sich ein starrer Körper auf vier Punkten ab (= Vierpunktstützung), handelt es sich um ein einfach statisch unbestimmtes System. Ist jedoch die Rahmenkonstruktion nachgiebig bzw. erfolgt die Abstützung gefedert und/oder ist die Belastung relativ hoch, können die Auflagerkräfte näherungsweise wie folgt berechnet werden.
Lösung der Aufgabe mittels Rechner und Überlagerung
Zur Lösung dieser Aufgabe benötigt man den Rechner zur Ermittlung der Auflagerkräfte bei Vierpunkt-Stützung. Bei den zwei folgenden Abbildungen handelt es sich um Screenshots dieses Rechners.
Zunächst rechnet man alle Längeneinheiten in eine gemeinsame Einheit um, wobei egal ist, welche Einheit man wählt. Die Maße in cm lauten: a = 100 cm, b = 80 cm, x = 20 cm und y = 10 cm. Ähnliches gilt auch für die Belastung: Jene Einheit, die für die Last F benützt wird, kommt für die vier Aufstandskräfte heraus. Daher muss man F nicht von kg in kN umrechnen.
Die umgerechneten Maße und die Belastung von 80 kg (= Masse der Person) setzt man in den Rechner ein. Man erhält die im Screenshot zu sehenden Belastungen in den vier Auflagerpunkten, wobei in diesem Fall natürlich kg heraus kommen:
A = 9 kg, B = 21 kg, C = 35 kg und D = 15 kg.
Als Nächstes werden die beiden Abstände x und y gleich 0 gesetzt, da das Eigengewicht in der Mitte des Tisches wirkt. Die Belastung beträgt jetzt 20 kg.
Man erhält die Belastungen in den vier Aufstandspunkten, aufgrund der Symmetrie sind sie gleich groß und betragen jeweils ein Viertel der Eigenmasse:
A = B = C = D = 5 kg.
Um die gesamten Belastungen in den 4 Aufstandspunkten zu bekommen, müssen die Teilbelastungen noch addiert werden (= Superposition):
A = 9 kg + 5 kg --> A = 14 kg
B = 21 kg + 5 kg --> B = 26 kg
C = 35 kg + 5 kg --> C = 40 kg
D = 15 kg + 5 kg --> D = 20 kg
Seite erstellt am 03.08.2020. Zuletzt geändert am 20.07.2021.