Standsicherheit (Sicherheit gegen Kippen)
Auf dieser Seite findet man neben der Begriffsklärung die Formel zur Berechnung der Standsicherheit bzw. Kippsicherheit. Zudem wird gezeigt, wie man eine einfache Aufgabe grafisch lösen kann.
Im Anschluss folgt ein Beispiel, im Zuge dessen die Standsicherheit eines Gabelstaplers bestimmt wird.
Werbung
Grundlegendes
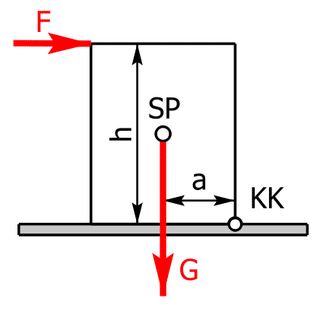
Die Abbildung zeigt einen einfachen Block unter horizontaler Krafteinwirkung. SP ist die Bezeichnung für den Schwerpunkt des Körpers.
Der Körper bleibt bei stetiger Zunahme der Kraft F zunächst in Ruhe. Erst wenn die Kraft F eine entsprechende Größe erreicht hat, wird der Körper entweder um die Kippkante KK kippen oder wegrutschen. Welcher dieser beiden Fälle eintritt, hängt von den Abmessungen a und h bzw. der Größe der Haftreibungszahl µH zwischen Boden und Körper ab.
Link zu passender Unterseite:
- Rechner für Standsicherheit (Kippen) & Wegrutschen eines Blocks auf schiefer Ebene
Formel zur Berechnung der Standsicherheit (Kippsicherheit)
Mit der folgenden Formel kann die Standsicherheit SS berechnet werden:
| MS | Standmoment: Kraft, die dem Kippen des Körpers entgegen wirkt (meist Eigengewicht oder Ballastgewichte) mal Normalabstand (Abstand von der Kippkante zu dieser Kraft) |
| MK | Kippmoment: Kraft, die den Körper um die Kippkante KK kippen will, mal Normalabstand (Abstand von der Kippkante zu dieser Kraft) |
Die beiden Momente können auch aus mehreren Einzelmomenten zusammengesetzt sein. Für die Standsicherheit SS gilt:
SS < 1 kippen
SS = 1 Kippgrenze
SS > 1 kein kippen
Du benötigst Nachhilfe im Raum Wien?
Ich helfe Dir!
Grafische Untersuchung des Kippens - Beispiel Block
Viele Aufgaben lassen sich auch grafisch lösen. Das wird am Beispiel eines einfachen Blocks gezeigt, auf den die Kräfte G und F wirken. G ist die Gewichtskraft und bleibt immer gleich groß, F wird hingegen variiert. Je nach Größe von F sind folgende drei Fälle möglich, wenn ein Wegrutschen ausgeschlossen werden kann:
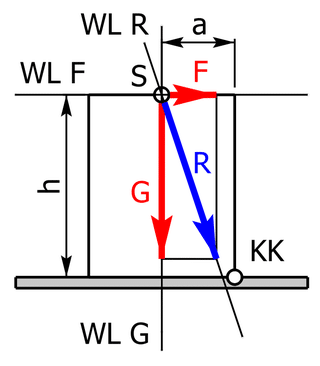
| WL F | Wirkungslinie von F |
| WL G | Wirkungslinie von G |
| WL R | Wirkungslinie der Resultierenden R von F und G; sie muss durch den Schnittpunkt S der Wirkungslinien von F und G verlaufen. |
| KK | Kippkante |
| S | Schnittpunkt der Wirkungslinien von F und G |
Es gibt drei Möglichkeiten:
- Liegt der Schnittpunkt der Wirkungslinie von der Resultierenden R mit der Aufstandsfläche innerhalb der Aufstandsfläche, so wie es in der linken Abbildung dargestellt ist, kommt es zu keinem Kippen.
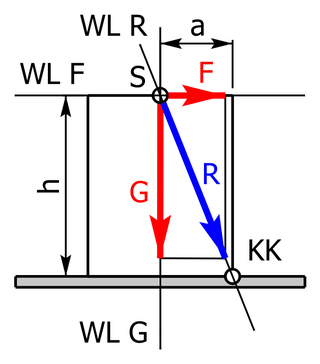
- Befindet sich dieser Schnittpunkt dagegen außerhalb, kippt der Block (rechtes Bild).
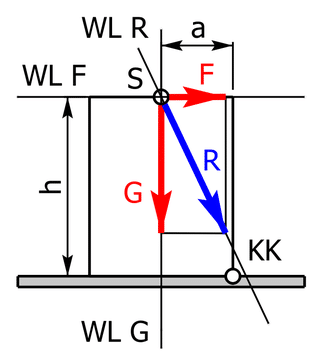
- Im mittleren Bild wird die Kippgrenze erreicht, da die Wirkungslinie der Resultierenden genau durch die Kippkante KK verläuft.
Beispiel: Berechnung Kippen eines Gabelstaplers
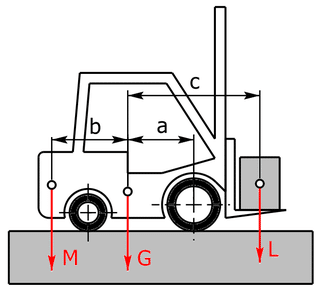
Man betrachte die nebenstehende Abbildung eines Gabelstaplers. Die Eigenmasse G beträgt 1300 kg, das Gegengewicht M hat eine Masse von 300 kg.
Die Längen lauten: a = 1,5 m, b = 1,75 m und c = 2,5 m.
- Um welchen Punkt wird der Gabelstapler bei Überlast kippen?
- Welche Last L darf der Gabelstapler heben, wenn eine Kippsicherheit von 1,3 gefordert wird? Das Ergebnis soll in Tonnen angegeben werden.
- Das Gegengewicht wurde ausgebaut. Welche Last kann der Gabelstapler nun heben, wenn die geforderte Standsicherheit wieder 1,3 betragen soll?
Lösung der Aufgabe
a) Kipppunkt
Der Gabelstapler kippt bei nicht angezogener Vorderradbremse um die Achse des Vorderrades, andernfalls um den Radaufstandspunkt dieses Rades.
b) Berechnung der Last L
Zuerst wird die Formel zur Berechnung der Standsicherheit benötigt. Mit den Standmomenten, dem Kippmoment und der Standsicherheit von 1.3 erhält man:
Nun wird die obige Gleichung zunächst mit L multipliziert und danach durch 1.3 dividiert bzw. es werden einfach die Plätze von L und 1.3 vertauscht:
Da das Ergebnis in Tonnen angegeben werden soll, rechnet man die Massen der Einfachheit halber nicht in Newton um. Einsetzen der gegebenen Zahlenwerte ergibt die gesuchte Last L:
c) Berechnung der Last L ohne Gegengewicht
Man verwendet die in b) hergeleitete Formel, nur dass der Wert für M jetzt Null ist:
Werbung
Seite erstellt im Jänner 2019. Zuletzt geändert am 24.11.2020.