Auf dieser Seite findest du ein Beispiel zur Berechnung des Massenträgheitsmoments einer Riemenscheibe, wobei auch der Satz von Steiner verwendet werden muss.
All jenen, die nur an der Berechnung der Massenträgheitsmomente von einfachen Körpern Interesse haben, ist der Besuch einer der beiden folgenden Unterseiten zu empfehlen:
Werbung
Aufgabe 1: Massenträgheitsmoment einer Riemenscheibe
Angabe
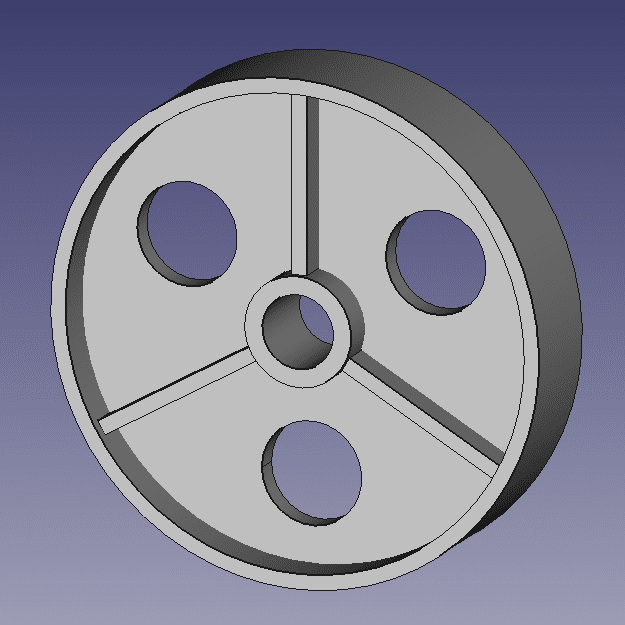
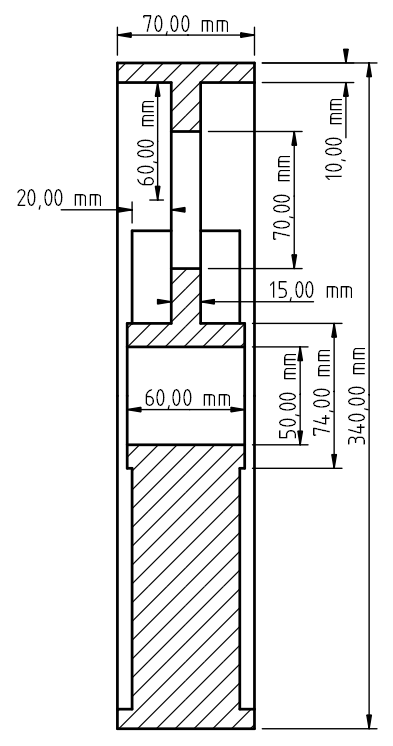
Es ist das Massenträgheitsmoment einer Riemenscheibe bezüglich ihrer Rotationsachse zu berechnen. Die Scheibe hat drei Löcher und zusätzlich auf jeder Seite je drei 10 mm starke Rippen. Die weiteren Abmessungen sind der nebenstehenden Zeichnung zu entnehmen. In der oberen Hälfte wird durch eines der Löcher geschnitten, während es sich in der unteren Hälfte um einen Schnitt durch zwei Rippen handelt. Die drei Löcher haben also laut Zeichnung einen Durchmesser von 70 mm. Bei den sechs Rippen handelt es sich um Quader mit der Dimension 20x10x123, da (340 – 74 – 10*2)/2 = 123 ist.
Die folgende Abbildung zeigt diese Scheibe in 3D:
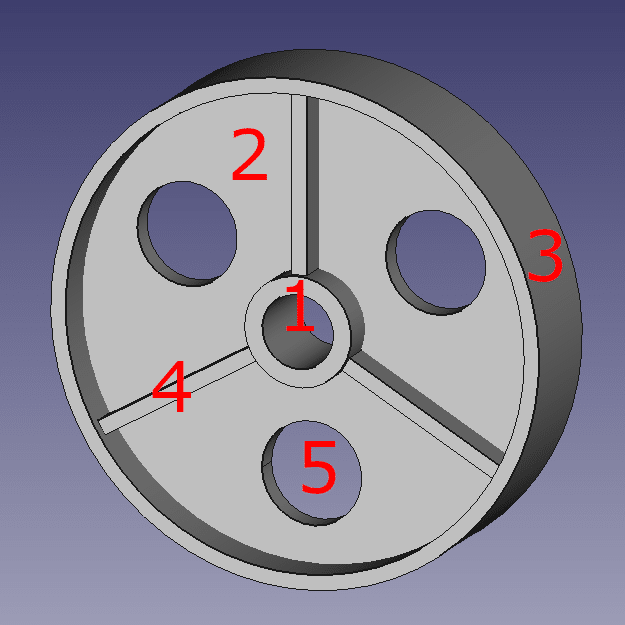
Aufteilung in 5 Teilkörper
Zunächst teilt man die Riemenscheibe in fünf Teilkörper auf:
- 1: Nabe
- 2: Scheibe
- 3: Kranz
- 4: Rippe (3x je Seite, also insgesamt 6x)
- 5: Loch (3x)
Bei der Nabe, der Scheibe und dem Kranz handelt es sich um Hohlzylinder. Die Rippen sind Quader und die Löcher einfache Zylinder.
Benötigte Formeln
Die Formeln zur Berechnung der Massenträgheitsmomente der Teilkörper findet man auf einer eigenen Unterseite. Die benötigten Formeln bezüglich der y-Achse (= Rotationsachse) werden hier nochmals angegeben. Bei der Formel für den Quader wird a statt h verwendet.
Vollzylinder
$$J_y=\frac{m \cdot r^2}{2}$$
Hohlzylinder
$$J_y=\frac{m \cdot (R^2+r^2)}{2}$$
Quader
$$J_y=\frac{m \cdot (a^2+b^2)}{12}$$
Wie man sieht, benötigt man zunächst die Massen der 5 Teilkörper. Die Masse m wird mit folgender Formel berechnet:
$$m=\rho \cdot V$$
Die Dichte ρ von Stahl beträgt ca. 7860 kg/m². Bei allen fünf Körpern handelt es sich um Quader, wobei es sich bei der Grundfläche um einen Kreis, Kreisringe und ein Rechteck handelt.
Das Volumen V eines Quaders ist die Grundfläche G multipliziert mit der Höhe h:
$$V=G \cdot h$$
Die Grundflächen werden dabei wie folgt berechnet:
Grundfläche eines Kreisrings
$$G_{Kreisring}=(R^2-r^2) \cdot \pi$$
Grundfläche eines Kreises
$$G_{Kreis}=R^2 \cdot \pi$$
Grundfläche eines Rechtecks
$$G_{Rechteck}=a \cdot b$$
Berechnung von Volumen und Masse der Teilkörper
Mit den obigen Formeln können nun die Volumina und die Massen der Teilkörper berechnet werden. Es ist dabei zu beachten, dass die Maße in mm angegeben sind und daher die Volumen mit 10-9 multipliziert werden müssen.
Volumen und Masse der Nabe (Teil 1, Grundfläche ist ein Kreisring):
$$V_1=\left[\left(\frac{74}{2}\right)^2-\left(\frac{50}{2}\right)^2\right] \cdot \pi \cdot 60=140240.7 mm^3$$
$$m=\rho \cdot V \Rightarrow m_1=7860 \cdot 140240.7 \cdot 10^{-9}=1.102kg$$
Volumen und Masse der Scheibe (Teil 2, Grundfläche ist ein Kreisring):
$$V_2=\left[\left(\frac{320}{2}\right)^2-\left(\frac{74}{2}\right)^2\right] \cdot \pi \cdot 15=1141859.0 mm^3$$
$$m_2=7860 \cdot 1141859.0 \cdot 10^{-9}=8.975kg$$
Volumen und Masse des Kranzes (Teil 3, Grundfläche ist ein Kreisring):
$$V_3=\left[\left(\frac{340}{2}\right)^2-\left(\frac{320}{2}\right)^2\right] \cdot \pi \cdot 70=725707.9 mm^3$$
$$m_3=7860 \cdot 725707.9 \cdot 10^{-9}=5.704kg$$
Volumen und Masse einer Rippe (Teil 4, Grundfläche ist ein Rechteck):
$$V_4=10 \cdot 20 \cdot 123=24600.0 mm^3$$
$$m_4=7860 \cdot 24600.0 \cdot 10^{-9}=0.193kg$$
Volumen und Masse eines Loches (Teil 5, Grundfläche ist ein Kreis):
$$V_5=\left(\frac{70}{2}\right)^2 \cdot \pi \cdot 15=57726.8mm^3$$
$$m_5=7860 \cdot 57726.8 \cdot 10^{-9}=0.454kg$$
Berechnung der einzelnen Massenträgheitsmomente
Jetzt ist es möglich, die Massenträgheitsmomente zu berechnen. Die Radien und die Längen sind in m umzurechnen und daher die jeweiligen Zahlen durch 1000 zu dividieren.
Massenträgheitsmoment der Nabe (Teil 1, Hohlzylinder):
$$J_y=\frac{m \cdot (R^2+r^2)}{2} \Rightarrow J_1=\frac{1.102 \cdot \left[\left(\frac {74}{2 \cdot 1000}\right)^2+\left(\frac {50}{2 \cdot 1000}\right)^2\right]}{2}$$
$$J_1=0.001099 kg \cdot m^2$$
Massenträgheitsmoment der Scheibe (Teil 2, Hohlzylinder):
$$J_y=\frac{m \cdot (R^2+r^2)}{2} \Rightarrow J_2=\frac{8.975 \cdot \left[\left(\frac {320}{2 \cdot 1000}\right)^2+\left(\frac {74}{2 \cdot 1000}\right)^2\right]}{2}$$
$$J_2=0.121023 kg \cdot m^2$$
Massenträgheitsmoment des Kranzes (Teil 3, Hohlzylinder):
$$J_y=\frac{m \cdot (R^2+r^2)}{2} \Rightarrow J_3=\frac{5.704 \cdot \left[\left(\frac {340}{2 \cdot 1000}\right)^2+\left(\frac {320}{2 \cdot 1000}\right)^2\right]}{2}$$
$$J_3= 0.155434kg \cdot m^2$$
Massenträgheitsmoment einer Rippe (Teil 4, Quader):
$$J_y=\frac{m \cdot (a^2+b^2)}{12} \Rightarrow J_4=\frac{0.193 \cdot \left[\left(\frac{10}{1000}\right)^2+\left(\frac{123}{1000}\right)^2 \right]}{12}$$
$$J_4=0.000245 kg \cdot m^2$$
Massenträgheitsmoment eines Loches (Teil 5, Vollzylinder):
$$J_y=\frac{m \cdot r^2}{2} \Rightarrow J_5=\frac{0.454 \cdot \left (\frac {70}{2 \cdot 1000} \right)^2}{2}=0.000278 kg \cdot m^2$$
Anwendung des Satz von Steiner
Die Schwerpunkte von Nabe, Scheibe und Kranz liegen alle auf der Rotationsachse und können daher einfach addiert werden. Die Schwerpunkte von den drei Löchern und von den sechs Rippen besitzen jedoch den Abstand d.4 bzw. d.5 zu dieser Rotationsachse, siehe Abbildung. Daher muss der Satz von Steiner angewandt werden, weil ja das Massenträgheitsmoment bezüglich dieser Achse berechnet werden soll.
Der Satz von Steiner lautet allgemein (weitere Erklärungen findet man auf einer eigenen Formelseite):
$$J_B=J+m \cdot d^2$$

Somit können die Trägheitsmomente bezüglich der Rotationsachse von einer Rippe (Teil 4) und von einem Loch (Teil 5) berechnet werden:
$$J_{B.4} = J_4 + m \cdot d_4^2 \Rightarrow J_{B.4}=0.000245+0.193 \cdot \left(\frac {123}{2 \cdot 1000}+\frac {74}{2 \cdot 1000} \right)^2$$
$$J_{B.4} = 0.00212 kg \cdot m^2$$
$$J_{B.5} = J_5 + m \cdot d_5^2 \Rightarrow J_{B.5}=0.000278+0.454 \cdot \left(\frac {340}{2 \cdot 1000}-\frac {10+60}{1000}\right)^2$$
$$J_{B.5} = 0.00482 kg \cdot m^2$$
Berechnung der Massenträgheitsmomente mit meinem Rechner
Die einzelnen Massenträgheitsmomente kann man auch ganz einfach und schnell mit meinem Rechner ermitteln. Die folgende Abbildung zeigt einen Screenshot des ausgefüllten Trägheitsmoment-Rechners für ein Loch (Teil 5).
Um den Steineranteil zu berücksichtigen, trägt man für den Abstand dy = 100 mm ein, da 340/2-10-60 = 100 ist. Man erhält natürlich dasselbe Ergebnis wie bei der Berechnung per Hand: Jy = JB.5 = 0.004815 kg*m2.

Gesamtes Massenträgheitsmoment bezüglich der Rotationsachse
Nun müssen nur noch alle Massenträgheitsmomente addiert bzw. subtrahiert (Löcher) werden. Achtung: Die Rippen und die Löcher sind mehrfach vorhanden!
$$J_{gesamt}=J_1+J_2+J_3+6 \cdot J_{B.4}-3 \cdot J_{B.5}$$
$$J_{gesamt}=0.001099+0.121023+0.155434+6 \cdot 0.00212-3 \cdot 0.00482$$
$$J_{gesamt}=0.27582 kg \cdot m^2$$
Werbung
Seite erstellt am 14.03.2021. Zuletzt geändert am 08.11.2021.