Diese Seite beschäftigt sich mit den Reibungskoeffizienten für ein Stahlrad auf einer Stahlschiene (Schienenfahrzeuge) sowie für einen Gummireifen auf Asphalt (Straßenfahrzeuge) bei verschiedenen Bedingungen.
Zudem findet man Informationen, wie sich die Haftreibungszahl mit zunehmender Geschwindigkeit (Curtius-Kniffler Kurve) bzw. bei einer Kurvenfahrt (Kammscher Kreis) ändert. Am Anfang wird auch kurz auf technische Einrichtungen in Straßenfahrzeugen wie ABS und ASR eingegangen.
Inhaltsverzeichnis
- Gleitreibungs- und Haftreibungsbeiwerte – Einführung
- Haftreibungszahlen für die Eisenbahn: Stahlrad auf Eisenbahnschiene (Haftreibung Stahl – Stahl)
- Haftreibungszahlen für die Straße: KFZ-Reifen auf fester Fahrbahn
- Zur Verfügung stehende Haftreibungszahl in Kurven beim Bremsen – Kammscher Kreis
Werbung
Haft- und Gleitreibungszahlen – Einführung
Bei den in den Tabellen angegebenen Werten handelt es sich immer nur um Richtwerte, da die Haftreibungszahl µH und die Gleitreibungszahl µG neben der Materialpaarung auch von der Geschwindigkeit, der Werkstoffoberfläche, der Normalkraft, der Aufstandsfläche, der Luftfeuchte und der Temperatur abhängen.
Es gilt fast immer, dass die Gleitreibungszahl etwas kleiner als die Haftreibungszahl ist. Deshalb gibt es bei Schienenfahrzeugen den sogenannten Gleitschutz. Er bewirkt, dass die Räder beim Bremsen nicht blockieren und dann auf der Schiene entlang gleiten. Mit dem Gleitschutz kann somit der Bremsweg verkürzt werden, außerdem verhindert er sogenannte Flachstellen auf den Rädern. Der Gleitschutz funktioniert ähnlich wie das ABS (Antiblockiersystem) beim Auto. Bei Kraftfahrzeugen sorgt das ABS zudem dafür, dass das Fahrzeug beschränkt lenkfähig bleibt.
Weiters sind die meisten Schienenfahrzeuge mit einem Schleuderschutz ausgestattet. Als Schleudern bezeichnet man das Durchdrehen der Räder bei zu schnellem Beschleunigen, das heißt, die Antriebskräfte übersteigen die Haftreibungskraft. Beim Auto wird dieses Problem mit Hilfe der sogenannten Antriebsschlupfregelung (ASR) gelöst.
Die Haftreibungszahlen spielen bei fast allen meinen Rechnern eine wichtige Rolle, weshalb ich auch diese Unterseite erstellt habe:
- Leistungs- und Zugkraftrechner
- Anhalte- und Bremswegrechner
- Beschleunigungsrechner
- Rechner für die zulässige Geschwindigkeit in Kurven
Recht weit verbreitete Irrtümer
- Die Haftreibungszahl ist stets kleiner gleich 1: Zum Beispiel haben Silikonkautschuk oder besonders weiche Gummireifen z. B. für die Formel 1 einen Haftreibungsbeiwert größer als eins!
- Schwere Fahrzeuge wie LKW haben einen wesentlich längeren Bremsweg als leichtere: Die Haftreibungszahl hängt nur relativ wenig von der Radlast ab, daher bestimmen in erster Linie die Leistungsfähigkeit der Bremsen und die Gummimischung der Reifen den Anhalteweg. LKW besitzen aus Gründen der Wirtschaftlichkeit Reifen aus einem härteren Gummi als PKW, was eine wesentlich höhere Lebensdauer der Reifen, dafür aber auch ein bisschen geringere Haftreibungszahlen zur Folge hat. Bei guten Bremsen wird ein LKW demnach einen etwas längeren Bremsweg als ein PKW haben. Im Gegensatz dazu hat ein Zug natürlich einen wesentlich größeren Bremsweg als ein PKW, da der Haftreibungsbeiwert zwischen Eisenbahnrad und Schiene viel kleiner als zwischen Gummireifen und Asphalt ist. Durch die Verwendung einer Magnetschienenbremse bzw. durch Sandstreuung (“Sanden”) bei ungünstiger Witterung kann der Bremsweg jedoch mitunter erheblich verkürzt werden.
Haftreibungszahlen für ein Stahlrad auf einer Stahlschiene
Die folgende Tabelle gibt die Haftreibungszahlen µH – auch Haftreibungskoeffizient oder Haftreibungsbeiwert genannt – für ein Stahlrad auf einer Stahlschiene bei verschiedenen Schienenzuständen an. Aus dieser Tabelle wird ersichtlich, dass die Haftreibungszahlen je nach Schienenzustand stark streuen können.
Bei nassen Schienen ist der Haftreibungskoeffizient um ca. 30 % kleiner als auf trockenen Gleisen. Reicht die vorhandene Haftreibung nicht aus, kann bei Bedarf gesandet werden. Es gilt zudem, dass der Haftreibungsbeiwert µH
- mit größerem Raddurchmesser zunimmt.
- mit steigender Geschwindigkeit abnimmt – siehe dazu auch das folgende Kapitel.
Zusätzlich ist zu beachten, dass vor allem in engen Kurven aufgrund des verstärkt auftretenden Schlupfes die übertragbare Kraft in Längsrichtung kleiner wird.
Tabelle Haftreibungszahlen Stahl auf Stahl (Eisenbahn)
| Schienenzustand | Haftreibungszahl µH |
| Laborbedingungen (extrem sauber, Vakuum) | bis 0.8 * |
| trocken | 0.20 – 0.35 (bis 0.45 beim Anfahren) |
| nass | 0.15 – 0.25 (bis 0.30 beim Anfahren) |
| feucht (Nebel, hohe Luftfeuchtigkeit, beginnender Regen) | > 0.10 ** |
| sehr schlechte Bedingungen (z. B. Ölfilm, Laub, Staub, Eis) | 0.05 – 0.10 ** |
| Schienenkopfschmierung mit HeadLub® (Firma Igralub) | 0.15 – 0.20 (0.20 = Herstellerangabe) |
| Betriebssituation | |
| Befahren von Rampen (Semmering, Lok 1144) | 0.25 (Boarische Wikipedia) |
| Bremsberechnung | 0.1 |
| Bremsen im Nahverkehr | ≤ 0.15 |
| Alle Werte gelten für den Haftreibungskoeffizienten Stahl auf Stahl! |
|
* Quelle: Roloff/Matek Maschinenelementeo
** unter Umständen ist ein Sanden erforderlich
Achtung:
Bei Verwendung von Rädern aus Gusseisen müssen die Haftreibungszahlen in etwa halbiert werden, da das im Gusseisen enthaltene Graphit als Schmiermittel wirkt!
Versuchsaufbau zur Ermittlung der Haftreibungszahl
Nachfolgend ein Bild meiner Gartenbahn 5 Zoll auf einer 35 % (!) steilen Versuchsstrecke, ein vorsichtiges Anfahren war gerade noch möglich. Das bedingt eine Haftreibungszahl von mindestens 0.35.
Durch die Schmierung der Kurven befand sich trotz intensiven Regens noch etwas Igralub auf der Schienenoberfläche, daher konnte ich den maximalen Haftreibungsbeiwert nicht ermitteln.

Welche Steigung kann ein Zug überwinden?
Wie obiger Versuch zeigt, könnten Fahrzeuge von reinen Adhäsionsbahnen, deren Achsen alle angetrieben sind, zumindest 35 % steile Strecken befahren. Allerdings sind diese Werte nur unter guten Bedingungen zu erreichen.
In der Praxis wurden Adhäsionsbahnen mit folgenden Steigungen ausgeführt:
- Straßenbahn Lissabon: 13.5 % (steilste Adhäsionsbahn der Welt)
- Pöstlingbergbahn Linz: 11.6 %
- Erzbergbahn: 7.1 %
Zahnradbahnen und Standseilbahnen können noch wesentlich steiler gebaut werden:
- Schafbergbahn: 25.5 % (klassische Zahnradbahn)
- Pilatusbahn: 48 % (spezielle Zahnradbahn)
- Standseilbahn Schwyz – Stoos: 110 %
Quelle Steigung: Wikipedia
Geschwindigkeitsabhängige Haftreibungszahl nach Curtius-Kniffler
Wie schon vorhin erwähnt, nimmt der Haftreibungsbeiwert mit steigender Geschwindigkeit ab. Für die Auslegung von Antrieben wird daher die folgende Formel verwendet, mit der die Haftreibungszahl in Abhängigkeit von der Geschwindigkeit berechnet werden kann:
$$µ_H=\frac{7.5}{V+44}+0.161$$
| µH |
Haftreibungskoeffizient |
| V | Geschwindigkeit in km/h |
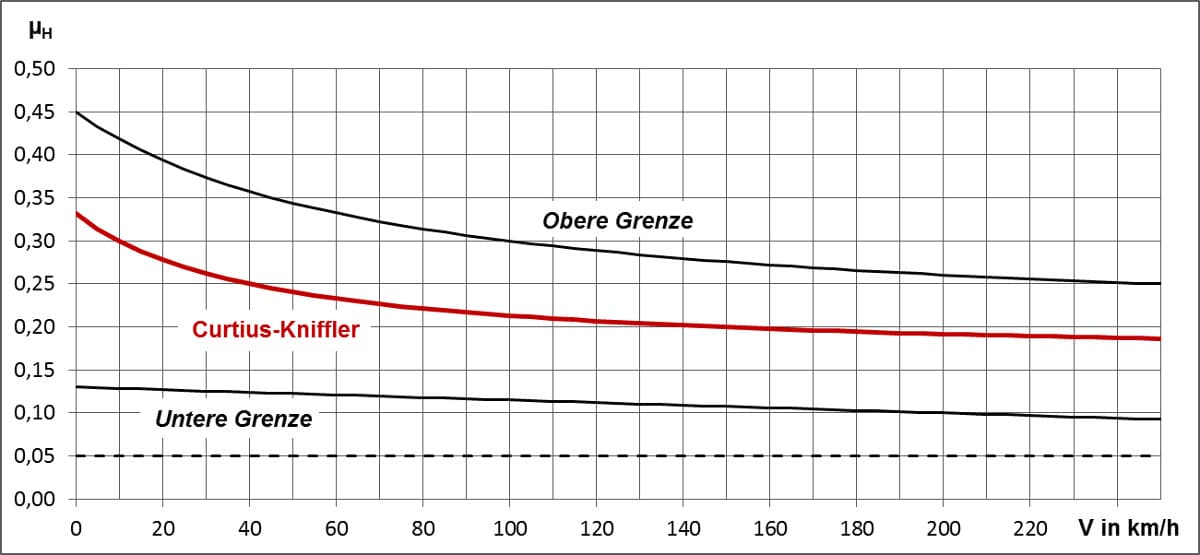
Das folgende Diagramm zeigt den Haftreibungsbeiwert in Abhängigkeit von der Geschwindigkeit, berechnet mit der Formel von Curtius-Kniffler. Zusätzlich sind die obere und die untere Grenze für alle Schienenzustände eingezeichnet. Im Extremfall – wie zum Beispiel bei öligen oder mit nassem Laub bedeckten Schienen – kann µH jedoch auch Werte bis zu 0.05 annehmen.
Bei modernen Triebfahrzeugen (Einzelachsantrieb, keine Zugkraftsprünge beim Anfahren) liegen die erreichbaren Haftreibungszahlen etwas über der Curtius-Kniffler Kurve.
Beispiele für Haftreibungsbeiwerte beim Anfahren
Den zum Anfahren erforderlichen Haftreibungskoeffizienten berechnet man wie folgt:
$$µ_H = \frac{Anfahrzugkraft}{g⋅Lokmasse}$$
| Lokomotive (ÖBB) |
Anfahrzugkraft in kN |
Masse in t |
Erforderliche Haft- reibungszahl µH |
| 1293 (Vectron) | 340 | 90 | 0.39 |
| 1016 bzw.1116 (Taurus) | 300 | 86 | 0.36 |
| 1042 bzw. 1142 | 260 | 83.5 | 0.32 |
| 1044 bzw. 1144 | 327 | 84 | 0.40 |
| 2016 (Herkules) | 235 | 80 | 0.30 |
| 2043 | 196 | 68 | 0.29 |
Beispiele für Haftreibungszahlen beim Befahren von Rampen
Die in der Tabelle angeführten Haftreibungsbeiwerte µH wurden mit meinem Zugkraftrechner bestimmt und gelten für die Semmeringbahn unter den folgenden Voraussetzungen:
- Die Steigung beträgt 25 ‰.
- Die Geschwindigkeit wird mit konstant 50 km/h angenommen.
- Die Bögen haben Kurvenradien von nur 190 m, der Krümmungswiderstand würde hier etwa 2 ‰ betragen. Da in den Bögen die Steigung jedoch geringer ist, wird dieser Widerstand nicht berücksichtigt.
| Lokomotive (ÖBB) |
Maximale Anhängelast laut Belastungstafel |
Benötigte Haft- reibungszahl µH |
Boarische Wikipedia ** |
| 1116 (Taurus) | 650 t | 0.23 | ? |
| 1144 | 600 t (650 t *) | 0.22 – 0.23 | 0.25 |
| 1142 | 500 t * | 0.19 | 0.22 |
* Quelle: Georg Schwach. (1981). Schnellzüge überwinden Gebirge. Wien: Verlag Josef Otto Slezak.
** Die Reibungszahlen aus der bayrischen Wikipedia beinhalten etwas Reserven zum Anfahren.
Kann unter ungünstigen Witterungsbedingungen die erforderliche Haftreibungszahl nicht erreicht werden, muss man sanden.
Haftreibungszahlen für einen KFZ-Reifen auf fester Fahrbahn
In der nächsten Tabelle findet man die Haftreibungszahlen für einen Gummireifen bei verschiedenen Straßenzuständen.
Folgendes ist bei der Auswahl des richtigen Wertes zu beachten:
- Bei einer Reibung zwischen Gummi und Straßenoberfläche tritt immer auch eine Verzahnung auf – abhängig vor allem von der Aufstandsfläche, der Normalkraft und der Temperatur – daher handelt es sich hier bei näherer Betrachtung eigentlich um keine Coulombsche Reibung.
- Die Werte variieren je nach Straßenzustand: bröckelnder Asphalt, Unebenheiten (führen zu einem Entlasten der Räder), Bodenmarkierungen, eventuelle Verschmutzungen durch Staub oder Öl.
- Der Haftreibungskoeffizient hängt neben dem Fahrbahnzustand auch von der verwendeten Gummimischung ab. Weiche Reifen haben generell eine bessere Haftung, dafür besitzen sie einen größeren Rollwiderstand und nützen sich schneller ab. Das gilt zum Beispiel auch für Reifen, die im Motorsport verwendet werden: sie erreichen Werte größer 1.5, zudem kann durch verschiedene Maßnahmen der Anpressdruck um ein Vielfaches gesteigert werden.
- Bei Kopfsteinpflaster ist die Haftung stets etwas kleiner als auf Beton bzw. Asphalt, das heißt, man muss in der Tabelle die kleineren Werte verwenden.
| Straßenzustand | Haftreibungszahl µH |
| trocken (allgemein) | 0.7 – 1 (Im Motorsport sind Werte über 1.5 möglich, zudem wird durch diverse Maßnahmen ein höherer Anpressdruck erreicht.) |
| trocken (PKW) | mindestens 0.8 |
| trocken (LKW) | mindestens 0.7 (etwas geringere Werte als beim PKW zugunsten höherer Laufleistung) |
| nass, aber kein Aquaplaning | 0.4 – 0.6 |
| nasses Laub, Schnee | 0.2 – 0.3 |
| bei Eis | ~ 0.1 |
| Aquaplaning | << 0.1 – Lenken bzw. Bremsen nur mehr sehr eingeschränkt möglich |
Wie aus der oberen Tabelle ersichtlich ist, wird der Haftreibungsbeiwert auf einer nassen Straße um rund 40 % kleiner. Bei einer Eisfahrbahn beträgt die Haftung nur mehr rund ein Zehntel des Wertes einer trockenen Fahrbahn!
Ob Aquaplaning auftritt, hängt hauptsächlich von der Fahrgeschwindigkeit, der Profiltiefe und der Breite des Reifens und der Wassertiefe auf der Fahrbahn ab.
Zur Verfügung stehender Haftreibungskoeffizient in Kurven beim Bremsen – Kammscher Kreis
Wenn man mit einem Fahrzeug in eine Kurve fährt, kann man weniger stark Bremsen bzw. Beschleunigen als in einem geraden Straßenabschnitt. Dieser Umstand wird anhand des nächsten Bildes ersichtlich, das den sogenannten Kammschen Kreis zeigt.
Zu beachten ist jedoch, dass der Kammsche Kreis nur ein idealisiertes Modell des vorliegenden Problems darstellt: Ein Reifen kann beispielsweise in Längsrichtung größere Kräfte wie in Querrichtung übertragen.
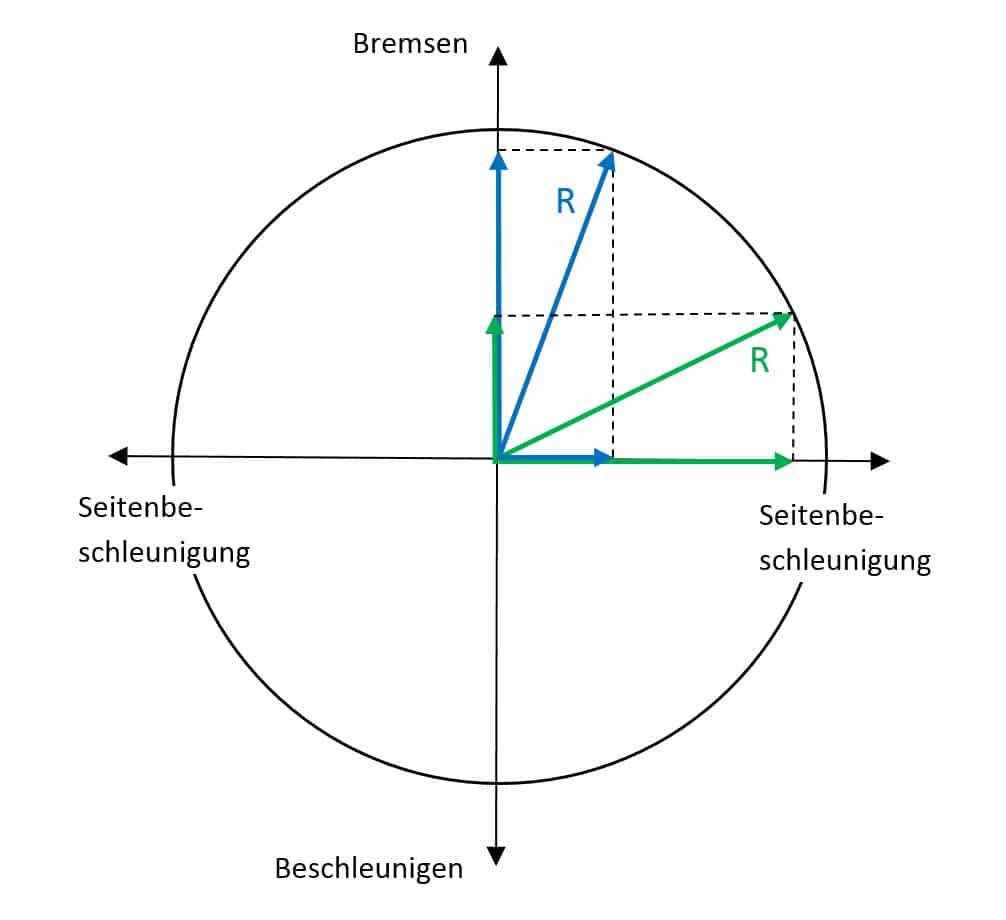
In der Skizze sind zwei Beispiele eingezeichnet:
- Variante 1 (blau): Geringe Seitenbeschleunigung aufgrund einer weiten Kurve oder einer langsamen Geschwindigkeit – es steht folglich viel Kraft für das Bremsen bzw. Beschleunigen zur Verfügung.
- Variante 2 (grün): Hohe Seitenbeschleunigung wegen einer engen Kurve oder einer großen Geschwindigkeit – für ein Verzögern bzw. Beschleunigen bleibt nur mehr wenig Kraft übrig.
Im Extremfall kann eine der beiden Komponenten auch null werden: Das bedeutet, dass man nur mehr geradeaus fahren bzw. überhaupt nicht mehr bremsen kann.
Der Radius des Kreises hängt vom Straßenzustand und von der Gummimischung des Autoreifens ab; bei einer trockenen Fahrbahn ist der Radius zum Beispiel viel größer als auf einer Schneefahrbahn.
Größer als µH mal Radaufstandskraft – diese Kraft entspricht genau dem Radius des Kammschen Kreises – kann die resultierende Kraft R, die zwischen Pneureifen und Straße übertragen werden muss, niemals werden. Wird die Kraft überschritten, kommt es zu folgenden Erscheinungen:
- Schieben oder Schleudern des Fahrzeuges in Kurven.
- Durchdrehen der Antriebsräder bei zu schnellem Beschleunigen.
- Blockieren der Räder bei zu starkem Bremsen.
Aufgrund des Lehrsatz des Pythagoras ergibt sich der folgende Zusammenhang:
$$(µ_H·Radaufstandskraft)^2=R^2=(F_{Seitenbeschleunigung}^2+(F_{Bremsen})^2$$
Anders angeschrieben:
$$µ_H^2=µ_q^2+µ_a^2$$
| µH | Von den Fahrbahnbedingungen abhängige Haftreibungszahl zwischen Rad und Straße. |
| µq | Haftreibungszahl, die für die Kurvenfahrt aufgrund der Seitenbeschleunigung benötigt wird. |
| µa | Haftreibungszahl, die für das Bremsen bzw. Beschleunigen gebraucht wird. |
Durch Umformen obiger Gleichung erhält man somit:
$$µ_q=\sqrt {µ_H^2-µ_a^2}\qquad µ_a=\sqrt {µ_H^2-µ_q^2}$$
Den Haftreibungskoeffizienten µH entnimmt man der oberen Tabelle. Mit dem Bremswegrechner wird µa ermittelt, µq bekommt man mit Hilfe des Rechners zur Bestimmung der Geschwindigkeit in Kurven.
Beispiel:
Es seien µH 0.8 und µq 0.6. Somit bleibt für das Bremsen nur mehr ein µa von 0.53 übrig!
Werbung
Seite erstellt wahrscheinlich im Jahr 2013. Zuletzt geändert am: