Hier finden Sie neben der Theorie auch die Herleitung der Formeln zur Berechnung des Flächenträgheitsmoments für einen Rechteck-Querschnitt und für ein I-Profil. Bei einer Herleitung des Flächenträgheitsmoments eines unsymmetrischen Querschnitts wird der Satz von Steiner verwendet.
All jenen, die nur an der Berechnung des Flächenträgheitsmoments von verschiedenen Profilen interessiert sind, ist eine der beiden folgenden Unterseiten zu empfehlen:
- Rechner für Flächenträgheits- und Widerstandsmomente
- Formeln wichtiger Flächenträgheitsmomente (Tabelle)
Inhaltsverzeichnis
Werbung
Einführung
Die übliche Einheit für das Flächenträgheitsmoment I ist cm4 oder mm4, es kann stets nur positive Werte annehmen. Eine alternative Bezeichnung dafür ist Flächenmoment 2. Grades.
Das Flächenträgheitsmoment wird für viele Anwendungen in der Mechanik verwendet. Man benötigt es zum Beispiel zur Berechnung des Widerstandsmoments und zur Untersuchung der Knicksicherheit von Stäben.
Formeln zur Berechnung des Flächenträgheitsmoments
Die Flächenträgheitsmomente Iy und Iz bezüglich der y- bzw. bezüglich der z-Achse sind wie folgt definiert:
$$I_y=\int_A z^2dA$$
$$I_z=\int_A y^2dA$$
| A | Fläche |
| y, z | Abstände |
Beispiel 1: Herleitung der Flächenträgheitsmomente für ein Rechteck
Damit man obige Formeln besser verstehen kann, erfolgt in dieser Aufgabe die Berechnung des Flächenträgheitsmoments eines Rechteckquerschnitts bezüglich der y-Achse. Der Flächeninhalt der mit dA bezeichneten Fläche beträgt:
$$dA = B · dz$$
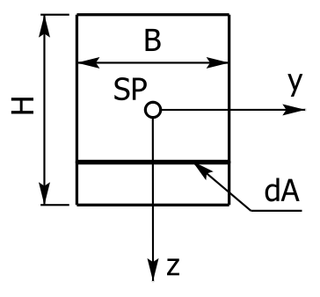
Nun benötigt man die Formel zur Berechnung des Flächenträgheitsmoments Iy bezüglich der y-Achse. Die Integrationsgrenzen sind -H/2 bzw. +H/2, mit Einsetzen für dA = B · dz und Kürzen erhält man das gesuchte Flächenträgheitsmoment:
$$I_y=\int_A z^2 dA=\int_{-\frac{H}{2}}^{\frac{H}{2}} (z^2·B)dz=\frac{1}{3}·B·\left[z^3\right]\big /_{-\frac{H}{2}}^{\frac{H}{2}}=\frac{1}{3}·B·\left[\left(\frac{H}{2}\right)^3-\left(-\frac{H}{2}\right)^3\right]$$
$$I_y=\frac{1}{3}·B·\left[\frac{H^3}{8}-\left(-\frac{H^3}{8}\right)\right]=\frac{1}{3}·B·\frac{2·H^3}{8}=\frac{B·H^3}{12}$$
Weitere Formeln wichtiger Flächenträgheitsmomente findet man in meiner Formelsammlung!
Flächenträgheitsmomente symmetrischer Flächen
Wenn die Schwerpunkte der Teilflächen und der Gesamtschwerpunkt auf einer Linie liegen, die zugleich meist die Symmetrielinie des Querschnitts ist, kann man die einzelnen Flächenträgheitsmomente addieren bzw. subtrahieren. Auf diese Weise können viele Flächenträgheitsmomente komplexerer Querschnitte sehr einfach berechnet werden.
Beispiel 2: Herleitung der Flächenträgheitsmomente eines I-Profils
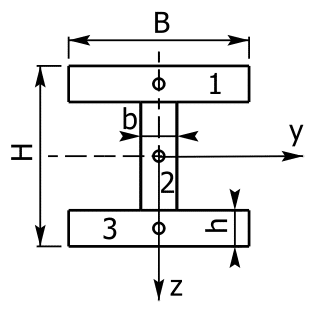
Das rechte Bild zeigt ein I-Profil, das um die beiden Koordinatenachsen symmetrisch ist.
Aufgabe: Es sollen die Flächenträgheitsmomente
- bezüglich der y- und
- bezüglich der z-Achse
hergeleitet werden.
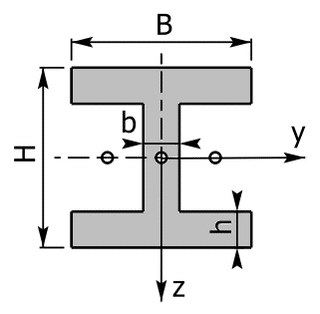
1) Herleitung des Flächenträgheitsmoments vom I-Profil bezüglich der y-Achse
Alle Schwerpunkte (gekennzeichnet durch Kreise) der Teilflächen liegen auf der y-Achse. Somit kann das Gesamtflächenträgheitsmoment durch Abzug der Teilflächenträgheitsmomente berechnet werden:
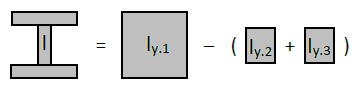
Es werden zunächst folgende Zusammenhänge definiert:
$$b_3 = B – b \qquad h_4 = H – 2 · h$$
Mit der in Beispiel 1 hergeleiteten Formel werden anschließend die Flächenträgheitsmomente der drei Teilflächen berechnet:
$$I_{y.1}=\frac{B · H^3}{12} \qquad I_{y.2}=I_{y.3}=\frac{(B-b) · (H-2 · h)^3}{2 · 12}=\frac{b_3 · h_4^3}{2 · 12}$$
Das Flächenträgheitsmoment des I-Trägers bezüglich der y-Achse lautet daher:
$$I_y=I_{y.1}-(I_{y.2}+I_{y.3})=I_{y.1}-2·I_{y.2}=\frac{B·H^3}{12}-2·\frac{b_3·h_4^3}{2·12}=\frac{B·H^3-b_3·h_4^3}{12}$$
2) Herleitung des Flächenträgheitsmoments vom I-Profil bezüglich der z-Achse
Auch hier liegen alle Schwerpunkte (gekennzeichnet durch Kreise) der Teilflächen auf einer gemeinsamen Linie, diesmal auf der z-Achse. Das Gesamtflächenträgheitsmoment wird durch Addition der Teilflächenträgheitsmomente berechnet:
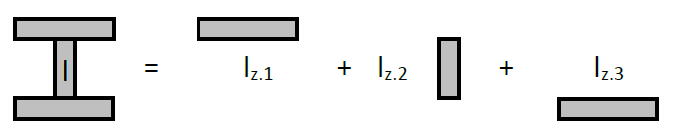
Es wird zuerst folgender Zusammenhang definiert:
$$h_4 = H – 2 · h$$
Nun werden mit der in Beispiel 1 hergeleiteten Formel die Flächenträgheitsmomente der einzelnen Teilflächen berechnet, wobei jedoch h und B zu vertauschen sind:
$$I_{z.1}=I_{z.3}=\frac{h·B^3}{12} \qquad I_{z.2}=\frac{(H-2·h)·b^3}{12}=\frac{h_4·b^3}{12}$$
Als Ergebnis erhält man durch Addition der drei Teilflächen das Flächenträgheitsmoment bezüglich der z-Achse:
$$I_z=I_{z.1}+I_{z.2}+I_{z.3}=2·I_{z.1}+I_{z.2}=2·\frac{h·B^3}{12}+\frac{h_4·b^3}{12}=\frac{2·h·B^3+h_4·b^3}{12}$$
Die in diesem Beispiel berechneten Flächenträgheitsmomente bezüglich der y- bzw. bezüglich der z-Achse stimmen mit den Formeln für ein I-Profil überein.
Flächenträgheitsmomente unsymmetrischer Flächen – Satz von Steiner
Falls die Querschnittsfläche unsymmetrisch ist, wird der Satz von Steiner benötigt. Das Flächenträgheitsmoment I der Gesamtfläche bezüglich einer gewählten Achse ist dann wie folgt zu berechnen, wobei die yi– bzw. zi-Achsen stets durch den Schwerpunkt der jeweiligen Teilfläche verlaufen müssen:
$$I=\sum(I_i+A_i·l_i^2)=I_1+A_1·l_1^2+I_2+A_2·l_2^2+…$$
| Ai | Flächeninhalt der Teilfläche i |
| li | Abstand zwischen den parallelen Achsen y und yi bzw. z und zi |
| Ii | Flächenträgheitsmoment der Teilfläche i bezüglich der yi– bzw. zi-Achse |
Ist die Lage des Gesamtschwerpunkts nicht bekannt, muss sie zunächst berechnet werden, siehe Seite Schwerpunkt von Flächen.
Beispiel 3: Flächenträgheitsmoment eines I-Profils mit Satz von Steiner
Es soll das Flächenträgheitsmoment bezüglich der y-Achse wie in Beispiel 2 berechnet werden, diesmal jedoch mit dem Satz von Steiner. Die Kreise in der Skizze bezeichnen wieder die Schwerpunkte der Teilflächen. Die beiden Teilflächen A1 und A3 sind aufgrund der Symmetrie gleich groß.
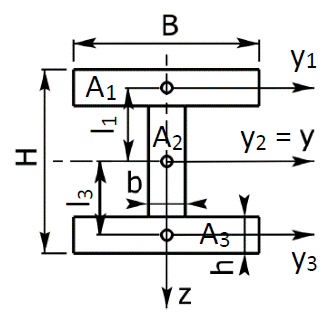
Lösung der Aufgabe:
Unter Verwendung des Satzes von Steiner kann das gesuchte Flächenträgheitsmoment berechnet werden:
$$I=\sum(I_i+A_i·l_i^2)=I_{y.1}+A_1·l_1^2+I_{y.2}+A_2·l_2^2+I_{y.3}+A_3·l_3^2$$
Zunächst müssen die einzelnen Komponenten ermittelt werden. Mit der in Beispiel 1 hergeleiteten Formel werden die Flächenträgheitsmomente bestimmt:
$$I_{y.1}=I_{y.3}=\frac{B·h^3}{12} \qquad I_{y.2}=\frac{b·(H-2·h)^3}{12}$$
Die drei Flächen lauten:
$$A_1 = B·h \qquad A_2 = b·(H – 2·h) \qquad H_3 = B·h$$
Nun kann das Gesamtflächenträgheitsmoment berechnet werden. Da die Flächen A1 und A3 ident sind, vereinfacht sich der Satz von Steiner etwas:
$$I_y=2·[I_{y.1}+A_1·l_1^2]+I_{y.2}+A_2·l_2^2=$$
$$I_y=2·\left[\frac{B·h^3}{12}+B·h·l_1^2\right]+\frac{b·(H-2·h)^3}{12}+b·(H-2·h)·l_2^2=$$
Die Länge l2 ist 0, da der Schwerpunkt von Teilfläche A2 auf der z-Achse liegt. Für die Länge l1 setzt man (H – h) / 2 ein. Zudem werden folgende Zusammenhänge definiert:
$$h_3 = H – h \qquad h_4 = H – 2 · h$$
Man erhält:
$$I_y=2·\left[\frac{B·h^3}{12}+B·h·\left(\frac{H-h}{2}\right)^2\right]+\frac{b·(H-2·h)^3}{12}=$$
$$I_y=\frac{2·B·h^3+6·B·h·h_3^2+b·h_4^3}{12}$$
Setzt man Zahlenwerte ein, sieht man, dass das Ergebnis mit dem in Beispiel 2 übereinstimmt. Dieses Aufgabe zeigt, dass bei symmetrischen Querschnitten besser wie in Beispiel 2 vorzugehen ist.
Werbung
Seite erstellt im Jänner 2019. Zuletzt geändert am 09.11.2021.