Auf dieser Seite wird zunächst erklärt, wie man den Flächenschwerpunkt einfacher und zusammengesetzter Flächen berechnen kann. Natürlich findet man auch die zur Berechnung benötigten Formeln.
Zuletzt wird die Lage des Schwerpunkts einer zusammengesetzten Figur (unsymmetrisches Rechteckhohlprofil) bestimmt, dieses Beispiel wird komplett durchgerechnet.
Inhaltsverzeichnis
- Einführung
- Einfache geometrische Flächen
- Zusammengesetzte Flächen
- Beispiel: Berechnung Flächenschwerpunkt eines Rechteckhohlprofils (nur um eine Achse symmetrisch)
Werbung
Einführung
Der geometrische Schwerpunkt von Flächen wird Flächenschwerpunkt genannt. Die Berechnung des Flächenschwerpunkts wird für einige Anwendungen in der Mechanik benötigt. Zum Beispiel kann bei Kenntnis der Lage des Gesamtschwerpunkts das Flächenträgheitsmoment komplexer Querschnitte bestimmt werden.
Falls eine Fläche Symmetrieachsen besitzt, liegt der Flächenschwerpunkt immer auf dieser bzw. auf diesen Symmetrieachsen. So befindet sich zum Beispiel der Schwerpunkt eines Rechtecks in der Mitte der Fläche, vergleiche Formel 4.1.
Einfache geometrische Flächen
In der folgenden Tabelle findet man die Lage des Schwerpunktes und die Formeln zur Berechnung des Schwerpunktabstandes von einfachen geometrischen Flächen. SP ist die Abkürzung für den Schwerpunkt, y0 bezeichnet den Schwerpunktabstand von einer Bezugskante bzw. von einem Bezugspunkt.
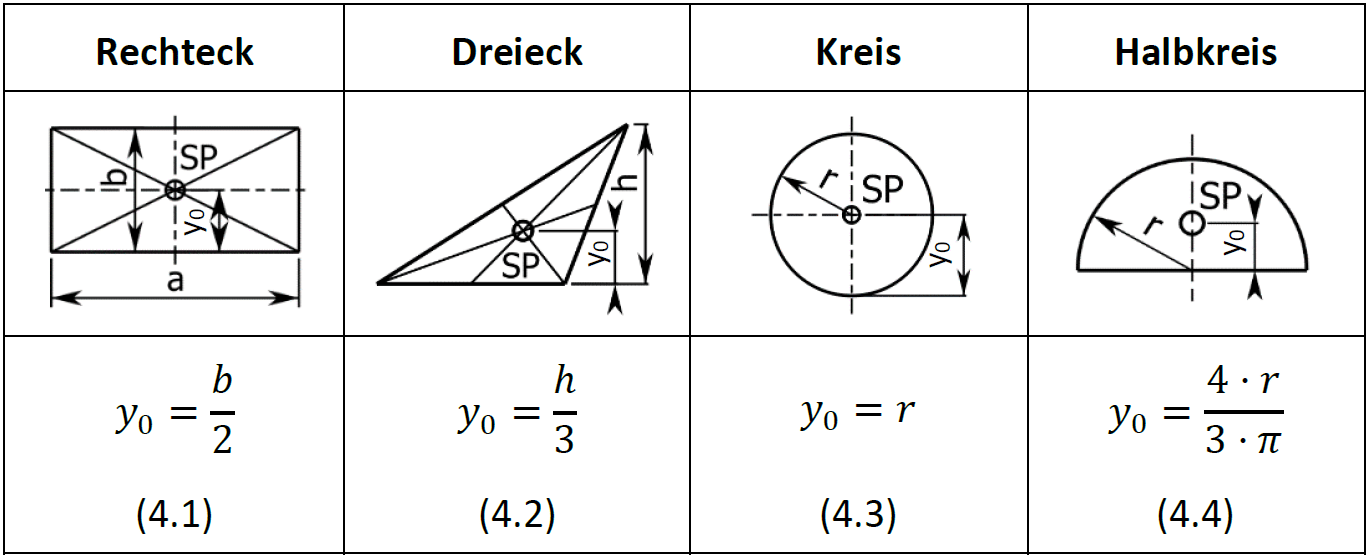
Formeln für zusammengesetzte Flächen
Falls man die Schwerpunktabstände komplexerer Flächen berechnen möchte, benötigt man die folgenden zwei Formeln.
Schwerpunktabstand x0 in Richtung der x-Achse (Formel 4.5):
$$x_0=\frac{\sum x_i·A_i}{\sum A_i}=\frac{x_1·A_1+x_2·A_2+…}{A_1+A_2+…}$$
Schwerpunktabstand y0 in Richtung der y-Achse (Formel 4.6):
$$y_0=\frac{\sum y_i·A_i}{\sum A_i}=\frac{y_1·A_1+y_2·A_2+…}{A_1+A_2+…}$$
| xi, yi | Abstand: Schwerpunkt Teilfläche – Bezugskante, häufig in mm oder cm |
| Ai | Flächeninhalt der Teilfläche, häufig in mm² oder cm² |
Analog dazu bestimmt man den Schwerpunktabstand z0 in Richtung der z-Achse.
Die Flächen bzw. Abstände können unter gewissen Umständen auch negative Werte annehmen:
- Je nach Lage der Bezugskante ist es möglich, dass Teilschwerpunktabstände und/oder der gesamte Schwerpunktabstand ein negatives Vorzeichen bekommen.
- Hat die Fläche Bohrungen oder andere Ausschnitte, werden diese Flächen in der Formel mit einem negativen Vorzeichen versehen.
Beispiel: Teilweise unsymmetrisches Rechteckhohlprofil
Dieses Beispiel wird komplett durchgerechnet, wobei die Bestimmung der Lage des Gesamtschwerpunkts nach der zuvor beschriebenen Vorgangsweise erfolgt.
Angabe
Bestimmen Sie die Lage des Schwerpunkts vom gegebenen unsymmetrischen Rechteckhohlprofil!
Die strichlierte Linie stellt die Symmetrieachse der Fläche dar, mit SP wird der Schwerpunkt bezeichnet. Alle Maße werden in mm angegeben.
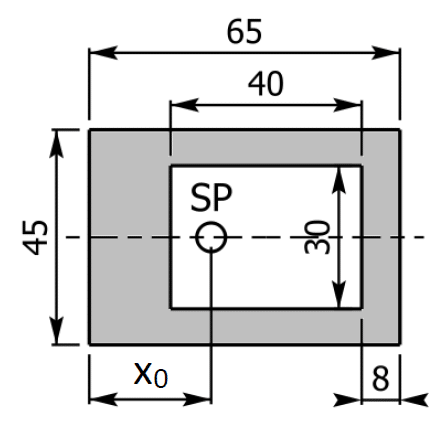
Lösung der Aufgabe
Aufteilung in zwei Teilflächen
Die Gesamtfläche wird in zwei Teilflächen aufgeteilt: Die Fläche des äußeren Rechtecks bekommt die Nummer 1, die innere Fläche die Nummer 2. Die innere Fläche wird abgezogen, deshalb erhält sie ein negatives Vorzeichen.

Wahl der Bezugskante, Anfertigung einer Skizze und Erstellung einer Tabelle
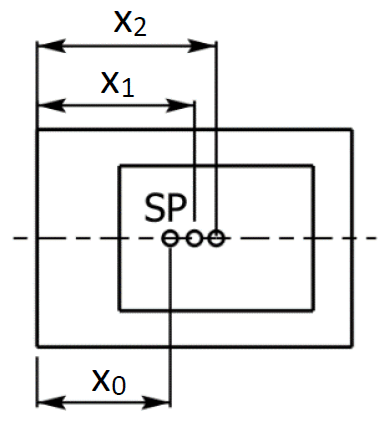
Anschließend werden eine Tabelle und eine Skizze erstellt, wobei i die Nummer der jeweiligen Teilfläche ist. Als Bezugskante wird die äußerste linke Seite des Profils gewählt. Von dieser Kante aus werden die zwei Abstände x1 und x2 zu den beiden Teilschwerpunkten bzw. der Abstand x0 zum Gesamtschwerpunkt ermittelt.
| i | Ai in mm2 | xi in mm | Ai · xi in mm3 |
| 1 | A1 = 2925 | x1 = 32.5 | A1 · x1 = 95062.5 |
| 2 | A2 = -1200 | x2 = 37.0 | A2 · x2 = -44400 |
| Σ | A = 1725 | 50662.5 |
Die Werte in den einzelnen Feldern dieser Tabelle werden auf folgende Weise bestimmt:
Flächeninhalte:
Äußere Teilfläche 1: A1 = 65 mm·45 mm = 2925 mm2
Innere Teilfläche 2: A2 = 40 mm·30 mm = -1200 mm2; Diese Fläche muss ein negatives Vorzeichen bekommen.
Gesamtfläche: A = A1 + A2 = 2925 mm2 – 1200 mm2 = 1725 mm2; Hier wird die Summe der beiden Teilflächen eingetragen, wobei in diesem Fall die innere Fläche von der ersten Fläche abgezogen wird.
Schwerpunktabstände:
Das sind die Abstände von der Bezugskante zu den Schwerpunkten der Teilflächen:
x1 = 65 mm / 2 = 32,5 mm
x2 = (65 mm – 40 mm – 8 mm) + 40 mm / 2 = 37 mm
Produkte aus Flächeninhalt und Schwerpunktabstand:
A1·x1 = 2925 mm2·32,5 mm = 95062,5 mm3
A2·x2 = -1200 mm2·37 mm = -44400 mm3
A1·x1 + A2·x2 = 95062,5 mm3 – 44400 mm3 = 50662,5 mm3
Berechnung der Lage des Gesamtschwerpunktes
Nun hat man alle erforderlichen Zwischenergebnisse und kann daher den gesuchten Gesamtschwerpunktabstand mit Formel 4.5 berechnen:
$$x_0=\frac{\sum x_i·A_i}{\sum A_i}=\frac{50662.5 \ mm^3}{1725 \ mm^2}=29.37 \ mm$$
Plausibilitätskontrolle:
Der Gesamtschwerpunkt liegt etwas links vom Halbierungspunkt der längeren Außenseite:
29.37 mm < 32.5 mm.
Variante: Aufteilung in vier Teilflächen
Für die Berechnung der Lage des Gesamtschwerpunktes gibt es für viele Aufgaben meist mehrere Möglichkeiten. Man könnte die gegebene Fläche auch in vier Teilflächen aufteilen:

Zunächst wird eine Tabelle erstellt. Die Beschriftung der Flächen ist in der folgenden Abbildung ersichtlich. Als Bezugskante wird wie schon zuvor die äußerste linke Kante gewählt.

Die Berechnung der Werte in den einzelnen Feldern erfolgt ähnlich wie zuvor, es wird jedoch auf die Anführung des genauen Rechenweges verzichtet. Wie man sieht, entsprechen diese Werte genau den Zahlen aus der vorigen Variante. Allerdings ist die zweite Variante wesentlich komplizierter und daher nicht zu empfehlen.
Werbung
Seite erstellt im November 2018. Zuletzt geändert am 09.11.2021.