Auf dieser Seite finden Sie Theorie, Formeln und drei recht umfangreiche Beispiele zum Satz von Castigliano und Menabrea: Es werden die Durchbiegung bzw. der Neigungswinkel eines einseitig eingespannten Balkens mit Gleichlast, die Auflagerreaktionen eines 3-fach statisch unbestimmten Systems und eine Auflagerkraft eines 1-fach statisch unbestimmt gelagerten Balkens berechnet.
Links zu weiteren Unterseiten:
- Balken-Rechner
- Formelsammlung: Berechnung der Auflagerreaktionen, Neigungswinkel & Durchbiegung
Inhaltsverzeichnis
- Der Satz von Castigliano
- Der Satz von Menabrea
- Sonderfall: Normalkraft N = 0
- Beispiel 1: Einseitig eingespannter Träger mit Gleichlast
- Maximale Durchbiegung – 1. Anwendung des Satzes von Castigliano
- Neigungswinkel in B – 2. Anwendung des Satzes von Castigliano
- Beispiel 2: Beidseitig eingespannter Träger mit Gleichlast
- Berechnung des Biegemoments – allgemein
- Einspannmoment MA – 1. Anwendung des Satzes von Menabrea
- Berechnung der Auflagerreaktionen in A
- Berechnung des maximalen Biegemoments
- Berechnung der Auflagerreaktionen in B
- Beispiel 3: Einseitig eingespannter Träger mit Loslager
Werbung
Der Satz von Castigliano
Mit dem Satz von Castigliano werden die Verschiebungen (Durchbiegung) bzw. Verdrehungen (Neigungswinkel) berechnet. Wenn an der untersuchten Stelle keine Kraft bzw. kein Moment wirkt, setzt man dort eine Hilfskraft bzw. ein Hilfsmoment an.
Verschiebung (Gleichung 1)
$$u_i=\frac{\partial U^{\#}}{\partial F_i}\qquad u_0= \frac{\partial U^{\#}}{\partial F^{\#}} \bigg/ _{F^{\#}=0}$$
Verdrehung (Gleichung 2)
$$\alpha_i=\frac{\partial U^{\#}}{\partial M_i}\qquad \alpha_0= \frac{\partial U^{\#}}{\partial M^{\#}} \bigg/ _{M^{\#}=0}$$
Dabei bedeuten:
| ui bzw. u0 | Verschiebung |
| αi bzw. α0 | Verdrehung, in Radiant (rad) |
| U# | Formänderungsenergie |
| Fi | äußere Kraft |
| Mi | äußeres Moment |
| F# | Hilfskraft |
| M# | Hilfsmoment |
Formänderungsenergie
Die Formänderungsenergie U# bekommt man mit folgender Gleichung (ohne Anteile von Temperatur und Federn, Gleichung 4):
$$U^{\#}=\frac{1}{2}\int_0^l\left[\frac{M_y^2}{E·J}+\frac{N^2}{E·A}\right]dx$$
Dabei bedeuten:
| U# | Formänderungsenergie |
| 0 bis l | Länge des Abschnitts, für den My und N gelten |
| My | Biegemoment |
| N | Normalkraft |
| E | E-Modul |
| J | Flächenträgheitsmoment |
| A | Querschnittsfläche |
Der Satz von Menabrea
Der Satz von Menabrea kann zur Berechnung der Auflagerreaktionen von statisch unbestimmten Systemen angewandt werden. Er ist ein Spezialfall des Satzes von Castigliano, da in einem Festlager die Verschiebungen bzw. bei einer festen Einspannung auch die Verdrehungen null sein müssen (Gleichung 3):
$$\frac{\partial U^{\#}}{\partial X_i}=0$$
Dabei bedeuten:
U# Formänderungsenergie
Xi statisch unbestimmte Größen
Die Formänderungsenergie erhält man mit derselben Formel wie beim Satz von Castigliano:
$$U^{\#}=\frac{1}{2}\int_0^l\left[\frac{M_y^2}{E·J}+\frac{N^2}{E·A}\right]dx$$
Sonderfall: Normalkraft N = 0
Ist die Normalkraft N gleich null bzw. wird sie vernachlässigt, können die obigen Gleichungen vereinfacht angeschrieben werden, was am Beispiel von Gleichung 1 gezeigt wird:
Gleichung 5a
$$ u_0= \frac{\partial U^{\#}}{\partial F^{\#}} \bigg/ _{F^{\#}=0}=\frac{1}{E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial F^{\#}}\right)dx \bigg/ _{F^{\#}=0}$$
Gleichung 5b
$$ u_i= \frac{\partial U^{\#}}{\partial F_i}=\frac{1}{E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial F_i}\right)dx$$
Beispiel 1: Einseitig eingespannter Träger mit Gleichlast
In dieser Aufgabe ist für einen statisch bestimmten Balken Folgendes zu berechnen:
- die maximale Durchbiegung
- der Neigungswinkel in B
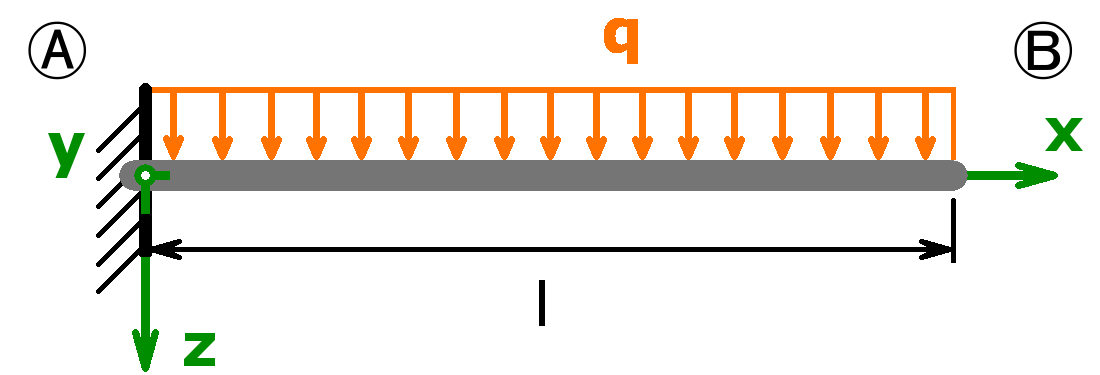
Maximale Durchbiegung – 1. Anwendung des Satzes von Castigliano
Als Erstes durchtrennt man den Balken, damit das zur Berechnung der maximalen Durchbiegung benötigte Biegemoment sichtbar wird. Die maximale Durchbiegung tritt am Ende des Balkens, also in B auf. Weil dort keine Kraft wirkt, setzt man an dieser Stelle eine Hilfskraft F# an:
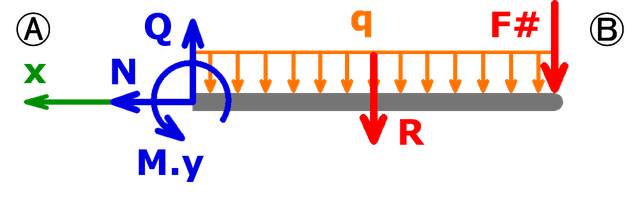
Nun bildet man die Summe der Momente an der Stelle des Schnittes. Durch Umformen erhält man das gesuchte Biegemoment, wobei die Resultierende R der Gleichlast durch q*x ersetzt werden kann:
$$\sum M=M_y-R·x-F^{\#}·x=0\Rightarrow M_y=q·x·\frac{x}{2}+F^{\#}·x$$
$$M_y=\frac{q·x^2}{2}+F^{\#}·x$$
Die benötigte Gleichung 4 vereinfacht sich in diesem Fall etwas, da die Normalkraft N gleich 0 ist:
$$U^{\#}=\frac{1}{2}\int_0^l\left[\frac{M_y^2}{E·J}+\frac{N^2}{E·A}\right]dx\Rightarrow U^{\#}=\frac{1}{2·E·J}\int_0^lM_y^2dx$$
Anschließend wird der Satz von Castigliano (Gleichung 1) angewandt, wobei nach F# abzuleiten ist. Anwendung der Kettenregel und Vereinfachen ergibt Gleichung 5a:
$$u_0= \frac{\partial U^{\#}}{\partial F^{\#}}\bigg/ _{F^{\#}=0} \Rightarrow u_0=\frac{\partial}{\partial F^{\#}}\left(\frac{1}{2·E·J}\int_0^lM_y^2dx\right)\bigg/ _{F^{\#}=0}$$
$$u_0=\frac{2}{2·E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial F^{\#}}\right)dx\bigg/ _{F^{\#}=0}\Rightarrow u_0=\frac{1}{E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial F^{\#}}\right)dx\bigg/ _{F^{\#}=0}$$
Mit der partiellen Ableitung des Biegemoments nach F#
$$\frac{\partial M_y}{\partial F^{\#}}=x$$
erhält man nach Einsetzen des zuvor aufgestellten Biegemoments und anschließendem Vereinfachen:
$$u_0=\frac{1}{E·J}\int_0^l\left[\left(\frac{q·x^2}{2}+F^{\#}·x\right)·x\right]dx\bigg/ _{F^{\#}=0}=\frac{1}{E·J}\int_0^l\left[\frac{q·x^3}{2}+F^{\#}·x^2\right]dx\bigg/ _{F^{\#}=0}$$
F# kann man nun 0 setzen. Dann wird diese Gleichung nach x integriert und anschließend setzt man die beiden Integrationsgrenzen ein:
$$u_0=\frac{1}{E·J}\int_0^l\left(\frac{q·x^3}{2}\right)dx=\frac{1}{E·J}\left[\frac{q·x^4}{2·4}\right]\bigg/ _0^l\Rightarrow u_0=\frac{q·l^4}{8·E·J}$$
Neigungswinkel in B – 2. Anwendung des Satzes von Castigliano
Bei der Berechnung des Neigungswinkels in B geht man ähnlich wie bei der Ermittlung der maximalen Durchbiegung vor. Allerdings wird statt der Hilfskraft F# ein Hilfsmoment M# benötigt:
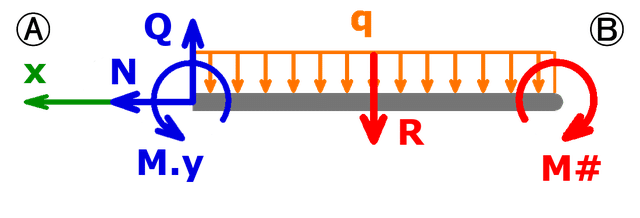
Das Biegemoment bekommt man wie schon zuvor mithilfe der Summe der Momente:
$$\sum M=M_y-R·x-M^{\#}=0\Rightarrow M_y=\frac{q·x^2}{2}+M^{\#}$$
Die partielle Ableitung des Biegemoments nach M# lautet:
$$\frac{\partial M_y}{\partial M^{\#}}=1$$
Anwenden des Satz von Castigliano ergibt:
$$\alpha_0=\frac{1}{E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial M^{\#}}\right)dx\bigg/ _{M^{\#}=0}=\frac{1}{E·J}\int_0^l\left[\left(\frac{q·x^2}{2}+M^{\#}\right)·1\right]dx\bigg/ _{M^{\#}=0}$$
M# setzt man nun 0. Anschließend wird diese Gleichung nach x integriert und dann setzt man die beiden Integrationsgrenzen ein. Man bekommt den Winkel in Radiant:
$$\Rightarrow \alpha_0=\frac{1}{E·J}\int_0^l\left(\frac{q·x^2}{2}\right)dx=\frac{1}{E·J}\left[\frac{q·x^3}{2·3}\right]\bigg/_0^l\Rightarrow\alpha_0=\frac{q·l^3}{6·E·J}$$
Werbung
Beispiel 2: Beidseitig eingespannter Träger mit Gleichlast
In dieser Aufgabe soll für den folgenden, 3-fach statisch unbestimmten Träger berechnet werden:
- die Auflagerreaktionen in A
- maximales Biegemoment
- die Auflagerreaktionen in B
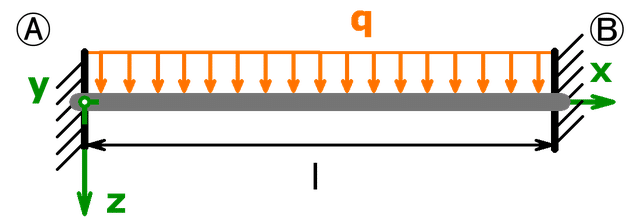
Berechnung des Biegemoments – allgemein
Als Erstes macht man das Lager A frei und durchtrennt den Balken, damit die gesuchten Schnittgrößen sichtbar und somit berechnet werden können:
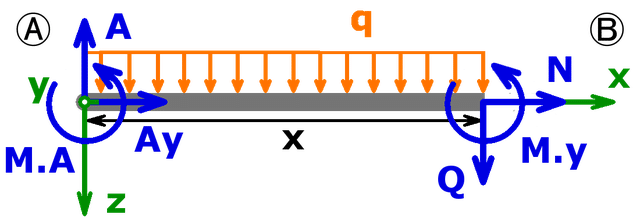
Nun kann das Biegemoment My bestimmt werden, wobei die Größen MA und A vorerst unbekannt sind:
$$M_A+M_y+q·x·\frac{x}{2}-A·x=0$$
durch Umformen erhält man Gleichung 6:
$$M_y(x)=A·x-\frac{q·x^2}{2}-M_A$$
Einspannmoment MA – 1. Anwendung des Satzes von Menabrea
Gleichung 4 vereinfacht sich wie schon bei der vorigen Aufgabe, da die Normalkraft N gleich 0 ist:
$$U^{\#}=\frac{1}{2}\int_0^l\left[\frac{M_y^2}{E·J}+\frac{N^2}{E·A}\right]dx\Rightarrow U^{\#}=\frac{1}{2·E·J}\int_0^l M_y^2dx$$
Anschließend wird der Satz von Menabrea (Gleichung 3) angewandt, wobei zunächst nach MA abzuleiten ist. Anwendung der Kettenregel und Vereinfachen ergibt (vgl. auch Gleichung 5b):
$$\frac{\partial U^{\#}}{\partial M_A}=0=\frac{\partial}{\partial M_A}\left(\frac{1}{2·E·J}\int_0^l M_y^2dx\right)=\frac{2}{2·E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial M_A}\right)dx$$
$$\Rightarrow\frac{\partial U^{\#}}{\partial M_A}=\frac{1}{E·J}\int_0^l\left(M_y·\frac{\partial M_y}{\partial M_A}\right)dx=0$$
Mit der partiellen Ableitung des Biegemoments nach MA
$$\frac{\partial M_y}{\partial M_A}=-1$$
ergibt sich nach Einsetzen des zuvor berechneten Biegemoments und anschließendem Vereinfachen:
$$\frac{1}{E·J}\int_0^l\left[\left(A·x-\frac{q·x^2}{2}-M_A\right)·(-1)\right]dx=-\frac{1}{E·J}\int_0^l\left(A·x-\frac{q·x^2}{2}-M_A\right)dx=0$$
Diese Gleichung wird nun nach x integriert (die Konstanten vor dem Integral kann man gleich weglassen), dann werden die beiden Integrationsgrenzen eingesetzt:
$$\left[\frac{A·x^2}{2}-\frac{q·x^3}{6}-M_A·x\right]\bigg/_0^l=\frac{A·l^2}{2}-\frac{q·l^3}{6}-M_A·l=0$$
Nach dem Umformen bekommt man für das Moment MA (Gleichung 7):
$$M_A=\frac{A·l}{2}-\frac{q·l^2}{6}$$
Das Problem ist, dass man die Auflagerkraft A noch nicht kennt. Aufgrund der Symmetrie kann man die Kraft in A jedoch sofort anschreiben, sie beträgt q*l/2 und ist natürlich genauso groß wie im Lager B.
Auflagerkraft A – 2. Anwendung des Satzes von Menabrea
Falls man das nicht erkennen sollte, kann die Kraft A wieder mit dem Satz von Menabrea berechnet werden, wobei diesmal nach A abgeleitet wird. Man erhält:
$$\frac{\partial U^{\#}}{\partial A}=0=\frac{\partial}{\partial A}\left[\frac{1}{2·E·J}\int_0^l\left(A·x-\frac{q·x^2}{2}-M_A\right)^2dx\right]$$
Mit
$$\frac{\partial M_y}{\partial A}=x$$
erhält man unter Anwendung der Kettenregel und mit anschließendem Vereinfachen:
$$=\frac{2}{2·E·J}\int_0^l\left[\left(A·x-\frac{q·x^2}{2}-M_A\right)·x\right]dx=\frac{1}{E·J}\int_0^l\left(A·x^2-\frac{q·x^3}{2}-M_A·x\right)dx=0$$
Diese Gleichung wird wieder nach x integriert, danach werden die beiden Integrationsgrenzen eingesetzt:
$$\left[\frac{A·x^3}{3}-\frac{q·x^4}{8}-\frac{M_A·x^2}{2}\right]\bigg/_0^l=0\Rightarrow\frac{A·l^3}{3}-\frac{q·l^4}{8}-\frac{M_A·l^2}{2}=0$$
Nun dividiert man noch die zuletzt erhaltene Gleichung durch l2:
$$\Rightarrow\frac{A·l}{3}-\frac{q·l^2}{8}-\frac{M_A}{2}=0$$
Berechnung der Auflagerreaktionen in A
Nun wird in die obige Gleichung das zuvor berechnete MA (Gleichung 7) eingesetzt:
$$\frac{A·l}{3}-\frac{q·l^2}{8}-\frac{1}{2}·\left(\frac{A·l}{2}-\frac{q·l^2}{6}\right)=0$$
Gleichung 8 erhält man durch Umformen für die Auflagerkraft A:
$$A=\frac{q·l}{2}$$
Durch Einsetzen von A (Gleichung 8) in Gleichung 7 kann auch das Moment MA bestimmt werden:
$$M_A=\frac{q·l}{2}·\frac{l}{2}-\frac{q·l^2}{6}=\frac{q·l^2}{12}$$
Berechnung des maximalen Biegemoments
Zuletzt wird das Biegemoment My(x) berechnet (Gleichung 8), indem man alle bekannten Größen in Gleichung 6 einsetzt:
$$M_y(x)=A·x-\frac{q·x^2}{2}-M_A=\frac{q·l}{2}·x-\frac{q·x^2}{2}-\frac{q·l^2}{12}$$
Die Stelle des maximalen Biegemoments bekommt man durch einmaliges Ableiten des Biegemoments nach x und anschließendem Nullsetzen. Es tritt natürlich in der Mitte des Balkens auf:
$$M’_y(x)=A·x-\frac{q·l}{2}-\frac{2·q·x}{2}=\frac{q·l}{2}-q·x=0\Rightarrow x=\frac{q·l}{2·q}\Rightarrow x=\frac{l}{2}$$
Das maximale Biegemoment in Balkenmitte erhält man, indem man l/2 für x einsetzt:
$$M_y\left(x=\frac{l}{2}\right)=\frac{q·l}{2}·\frac{l}{2}-\frac{q·\left(\frac{l}{2}\right)^2}{2}-\frac{q·l^2}{12}\Rightarrow M_{y.max}=\frac{q·l^2}{24}$$
Berechnung der Auflagerreaktionen in B
Um die Auflagerreaktionen in B zu bekommen, muss man zunächst den Balken freimachen:
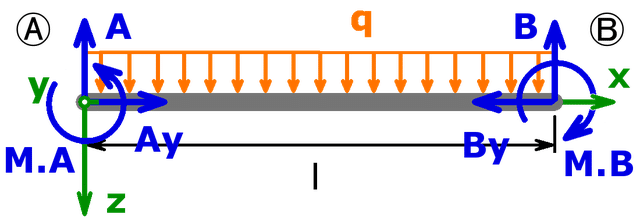
Anschließend werden das Kräftegleichgewicht in z-Richtung und das Momentengleichgewicht um den Punkt B aufgestellt:
$$\sum F_{i.z}=0=-A-B+q·l\Rightarrow B=q·l-A$$
$$\sum M_{B.i.y}=M_A-M_B-q·l·\frac{l}{2}+B·l\Rightarrow M_B=M_A-\frac{q·l^2}{2}+B·l$$
Durch Einsetzen für A bzw. B bekommt man die gesuchten Auflagerreaktionen in B:
$$B=q·l-\frac{q·l}{2}\Rightarrow B=\frac{q·l}{2}$$
$$M_B=M_A-\frac{q·l^2}{2}+\frac{q·l}{2}·l\Rightarrow M_B=M_A$$
Aufgrund der Symmetrie gilt also: MA = MB und A = B.
Beispiel 3: Einseitig eingespannter Träger mit Loslager
Es ist die Auflagerkraft im Loslager B des 1-fach statisch unbestimmten Balkens mit Gleichlast zu berechnen.
Hinweis:
Dieses Beispiel wird auch mittels Superpositionsprinzip gelöst!
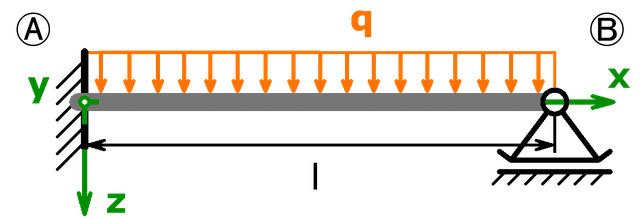
Berechnung des Biegemoments
Man betrachtet nur den rechten Teil des Balkens:
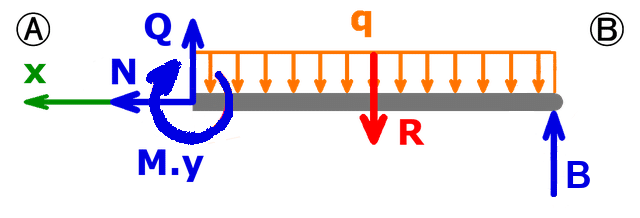
Das Biegemoment lautet:
$$M_y=B⋅x-\frac{q⋅x^2}{2}$$
Auflagerkraft B – Anwendung des Satzes von Menabrea
Wie schon zuvor verwendet man die vereinfachte Gleichung 5b. Die Verschiebung muss in diesem Fall 0 sein, da in vertikaler Richtung keine Verschiebung auftreten kann:
$$u_i=\frac{\partial U ^{\#}}{\partial B}=\frac{1}{E⋅J} \int_0^l \left (M_y⋅\frac{\partial M_y}{\partial B} \right )dx=0$$
Mit der partiellen Ableitung
$$\frac{∂M_y}{∂B}=x$$
und einsetzen erhält man:
$$\frac{1}{E⋅J}\int_0^l\left [\left( B⋅x−\frac {q⋅x^2}{2}\right )⋅x \right]dx=0$$
Da die Verschiebung 0 ist, kann man die Konstanten vor dem Integral weglassen. Ausmultiplizieren ergibt:
$$\int_0^l \left( B⋅x^2−\frac {q⋅x^3}{2}\right )dx=0$$
Durch Integrieren und Einsetzen der Grenzen bekommt man:
$$\left[\frac {B⋅x^3}{3}−\frac{q⋅x^4}{8}\right]_0^l=0⇒\frac{B⋅l^3}{3}−\frac{q⋅l^4}{8}=0$$
Kürzen und umformen ergibt die gesuchte Auflagerkraft B:
$$B=\frac{3⋅q⋅l}{8}$$
Werbung
Seite erstellt wahrscheinlich im November 2017. Zuletzt geändert am 11.11.2021.