Auf dieser Seite wird der Zusammenhang zwischen Weg, Geschwindigkeit, Beschleunigung und Ruck anhand von Diagrammen, Beispielen und Formeln bzw. Herleitungen ausführlich erklärt (Differenzieren bzw. Integrieren der verschiedenen Größen). Zudem wird der Unterschied zwischen Durchschnitts- und Momentan-Geschwindigkeit erläutert.
Abschließend findet man zu diesem Thema noch ein ausführliches praktisches Beispiel, wie es oft in der Schule vorkommt. Es werden unter anderem berechnet: Durchschnitts-, Anfangs-, Aufprall- und Momentangeschwindigkeit, Steigungen der Tangente (Differentialquotient) und Sekante (Differenzenquotient).
In diesem Zusammenhang sei auch auf meinen Bremswegrechner und die Formelsammlung hingewiesen!
Inhaltsverzeichnis
- Übersichtstabelle: Zusammenhang dieser vier Größen durch Integrieren bzw. Ableiten
- Berechnung von Ruck, Beschleunigung, Geschwindigkeit und Weg durch Integrieren
-
- Einfaches Beispiel: Bestimmung von Geschwindigkeit und Weg für eine konstante Beschleunigung
- Grafischer Zusammenhang – erklärt anhand eines einfachen Beispiels
- Berechnung dieser Größen durch Differenzieren – prinzizipielle Vorgehensweise
- Unterschied Durchschnitts- & Momentangeschwindigkeit
-
- Durchschnittsgeschwindigkeit (≙ Differenzenquotient)
- Momentangeschwindigkeit (≙ Differentialquotient)
-
- Kleines Beispiel: Berechnung des Differentialquotienten mit dem Limes
- Ausführliches Beispiel aus der (Schul-) Praxis, mit grafischen Darstellungen
-
- Angabe
- Lösungen der Aufgabe
- Geschwindigkeit-Zeit Diagramm mit Differenzen- und Differentialquotienten.
Werbung
Übersichtstabelle
Die folgende Tabelle zeigt den Zusammenhang zwischen Weg, Geschwindigkeit, Beschleunigung und Ruck durch Ableitung bzw. Integration:
| differenzieren f ´ (= ableiten) |
↓ | Weg s(t) | ↑ | integrieren ∫ |
| ↓ | Geschwindigkeit v(t) | ↑ | ||
| ↓ | Beschleunigung a(t) | ↑ | ||
| ↓ | Ruck | ↑ |
Die Geschwindigkeit v(t) ist also die Ableitung des Weges bzw. das Integral der Beschleunigung.
Es sei z. B. die Geschwindigkeit v(t) bekannt. Ist nun der Weg gesucht, muss man die Geschwindigkeit nach der Zeit t integrieren. Möchte man die Beschleunigung wissen, ist die Geschwindigkeit abzuleiten (= differenzieren).
Berechnung der Größen durch Integrieren – prinzipielle Vorgangsweise
Die Beschleunigung kann sowohl positiv als auch negativ (= Verzögerung oder Bremsen) sein. Die SI-Einheit der Beschleunigung ist m/s². Die Beschleunigung a(t) wird durch Integration des Rucks j(t) nach der Zeit t berechnet:
$$\vec{a}(t)=\int \vec{j}(t)dt$$
Die SI-Einheit der Geschwindigkeit ist m/s. Die Umrechnung von m/s in km/h ist einfach: Multipliziert man die Geschwindigkeit in m/s mit 3.6, so erhält man km/h. Die Geschwindigkeit v(t) bekommt man durch Integration der Beschleunigung a(t) nach der Zeit t:
$$\vec{v}(t)=\int \vec{a}(t)dt$$
Die SI-Einheit des Weges ist m. Der Weg s(t) wird durch Integration der Geschwindigkeit v(t) nach der Zeit t berechnet:
$$\vec{s}(t)=\int \vec{v}(t)dt$$
Einfaches Beispiel: Bestimmung von Geschwindigkeit und Weg (konstante Beschleunigung) durch Integrieren
Die Beschleunigung sei bekannt und betrage konstant a (das heißt, sie ist unabhängig von der Zeit t, der Ruck ist daher 0). Die Geschwindigkeit erhält man durch Integration der Beschleunigung:
$$v(t) = \int (a)dt = a⋅t + C$$
Zum Zeitpunkt t = 0 beträgt die Geschwindigkeit v0 (= Anfangsgeschwindigkeit). Das t in der obigen Gleichung wird somit durch 0 ersetzt, die Integrationskonstante C wird folglich zu v0, da der erste Term durch die Multiplikation mit 0 verschwindet:
$$v(0) = v_0 = a⋅0 + C \Rightarrow C = v_0$$
Daher lautet Gleichung 1 für die Geschwindigkeit v(t):
(vgl. Formeln mit Anfangsgeschwindigkeit, 3. Zeile, 2. Spalte)
$$v(t) = a⋅t + v_0$$
Integriert man die Geschwindigkeit nach der Zeit t, bekommt man den Weg:
$$s(t)=\int v(t)dt=\int(a·t+v_0)dt=\frac{a·t^2}{2}+v_0·t+C_1$$
Zum Zeitpunkt t = 0 sei der Weg s0. Damit ist die Integrationskonstante C1 = s0 und Gleichung 2 für den Weg s(t) lautet daher:
$$s(t)=\frac{a·t^2}{2}+v_0·t+s_0$$
Genau diese Formel wird in einem ausführlichen Beispiel weiter unten benötigt: h(t) = -10/2⋅t² + 20⋅t + 15. Der Luftwiderstand wird vernachlässigt. Man kann die einzelnen Werte direkt ablesen:
- Beschleunigung a = -10 m/s², das entspricht der gerundeten Erdbeschleunigung g. Sie ist in diesem Fall negativ, da sie der Bewegungsrichtung entgegen wirkt.
- Anfangsgeschwindigkeit v0 = 20 m/s
- Anfangsweg (≙ Höhe) s0 = 15 m
Oftmals ist jedoch zum Zeitpunkt t = 0 der Weg s0 null. In diesem Fall wird s0 zu 0, da alle Terme mit t wegfallen:
$$s(0) = \frac{a⋅0^2}{2} + v_0⋅0 + s_0 = 0 \Rightarrow s_0 = 0$$
Grafischer Zusammenhang – erklärt anhand eines Beispiels
Allgemeines:
Ein bestimmtes Integral berechnet in einem vorgegebenen Intervall stets die von der Kurve und der x-Achse eingeschlossene Fläche.
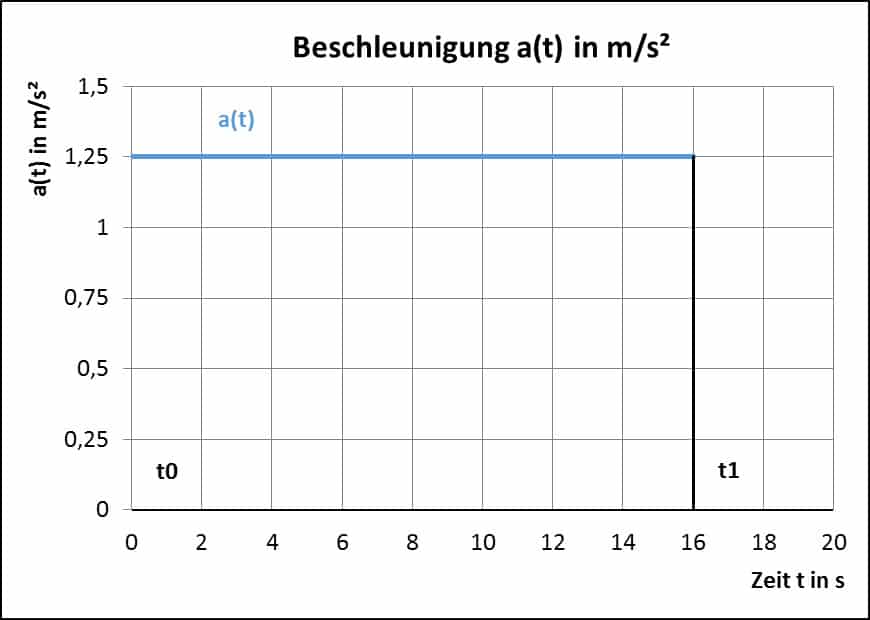
Die Fläche unterhalb der Beschleunigungsfunktion (Abbildung 1) im Intervall [t0; t1] ist die Änderung der Geschwindigkeit in diesem Intervall. Addiert man zu diesem Wert noch die Anfangsgeschwindigkeit v0 (das ist die Geschwindigkeit zum Zeitpunkt t0), erhält man die Geschwindigkeit zum Zeitpunkt t1.
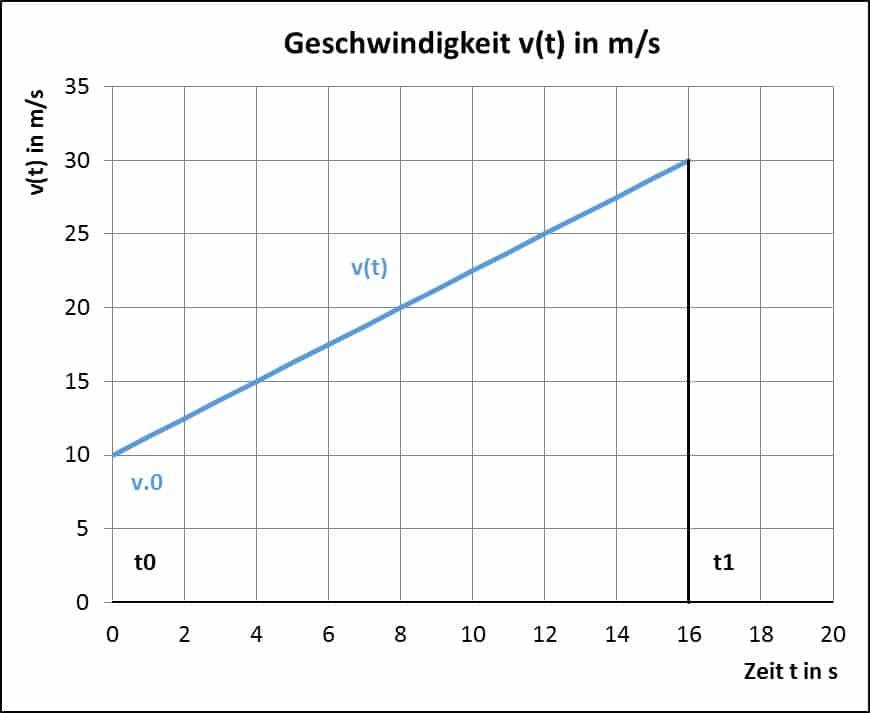
Die Fläche zwischen Kurve und x-Achse in Abbildung 2 entspricht dem im Intervall [t0; t1] zurückgelegten Weg. Eventuell vorhandene Anfangsbedingungen müssen stets berücksichtigt werden!
Angabe:
Die Beschleunigung sei konstant 1.25 m/s², die Anfangsgeschwindigkeit v0 beträgt 10 m/s. Gesucht sind die Geschwindigkeit und der Weg inklusive grafischer Darstellung.
Lösung:
Setzt man die beiden gegebenen Werte in die vorhin hergeleiteten Formeln ein, kann man die folgenden drei Diagramme zeichnen.
In Abbildung 1 sieht man die Beschleunigung a(t) in Abhängigkeit von der Zeit t.
Für die Geschwindigkeit v(t) ergibt sich mit der Anfangsgeschwindigkeit v0 = 10 m/s und Einsetzen der gegebenen Werte in Gleichung 1 die folgende Formel:
$$v(t) = 1.25⋅t + 10$$
Dieser lineare Zusammenhang ist in Abbildung 2 dargestellt. Aus dem Diagramm in dieser Abbildung bzw. mit Hilfe der Formel für v(t) kann die Geschwindigkeit zum Zeitpunkt t1 (t = 16 s) bestimmt werden:
$$v(16) = 1.25⋅16 + 10 = 30\ m/s$$
Alternative:
Die Fläche unterhalb der Funktion in Abbildung 1 im Intervall [t0; t1] ist: 1.25 m/s²⋅16 s = 20 m/s. Zum Zeitpunkt t0 beträgt die Anfangsgeschwindigkeit 10 m/s, dieser Wert wird zu 20 m/s addiert. Das ergibt 30 m/s. Dieser Wert entspricht der vorhin ermittelten Geschwindigkeit.
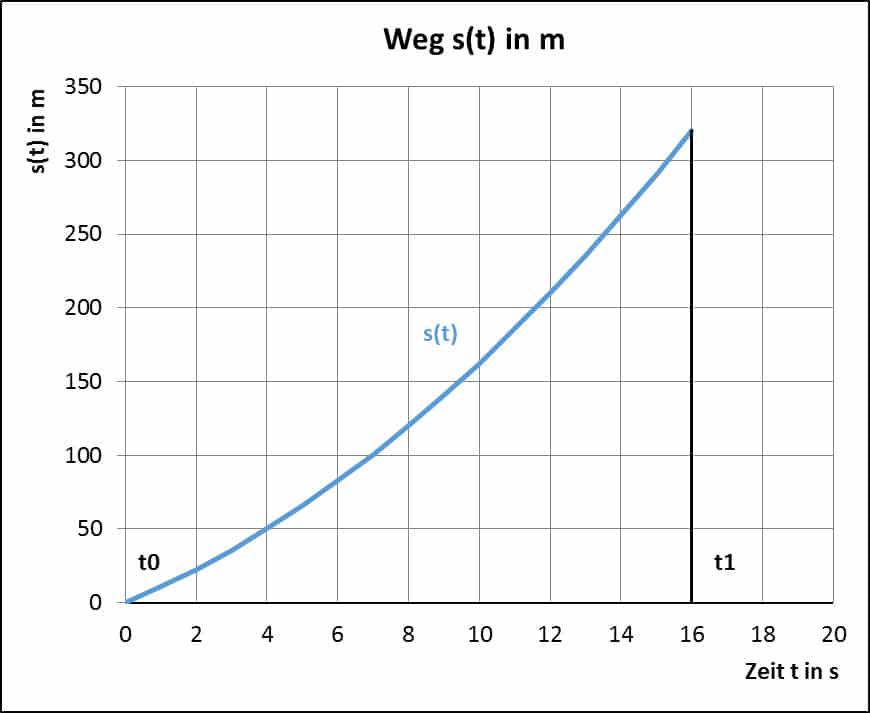
Die Formel für den Weg s(t) lautet:
$$s(t) = \frac{1.25}{2}⋅t^2 + 10⋅t$$
Obige Formel bekommt man durch Einsetzen der gegebenen Werte in Gleichung 2, wobei s0 null ist. Diese quadratische Funktion ist in Abbildung 3 zu sehen. Einsetzen für t = 16 s ergibt:
$$s(16) = \frac{1.25}{2}⋅16^2 + 10⋅16 = 320$$
Der Weg zum Zeitpunkt t1 (t = 16 s) beträgt somit 320 m.
Alternative:
Die Fläche unterhalb der Funktion in Abbildung 2 bestimmen. Dazu teilt man die Fläche in ein Rechteck und ein rechtwinkliges Dreieck auf:
$$A = a⋅b + \frac{b⋅h}{2} = \left(\frac{h}{2} + a\right)⋅b$$
Setzt man für a, b und h die entsprechenden Zahlenwerte ein, erhält man den zurückgelegten Weg:
$$\left(\frac{30-10}{2}+10\right)\ \frac{m}{s} ⋅ 16\ s=320\ m$$
Man kann diese Fläche natürlich auch durch Integrieren berechnen. Bei der Funktion in Abbildung 2 handelt es sich um eine Gerade. Die Geradengleichung lautet allgemein:
$$f(x) = k⋅x + d$$
Hier wird x durch t ersetzt: v(t) = k⋅t + d. Der Parameter d ist der Wert, wo die Gerade die y-Achse schneidet, in diesem Beispiel ist d gleich 10. Die Variable k bestimmt man mit dem Differenzenquotienten, also:
$$k = \frac{Δy}{Δt} = \frac{30-10}{16-0} = \frac{20}{16}= \frac{5}{4} $$
Nun hat man alle notwendigen Werte und man kann somit s(t) berechnen:
$$s(t) = ∫(v(t))dt = ∫\left(\frac{5}{4}⋅t + 10\right)dt = \frac{5}{8}⋅t^2 + 10⋅t + C$$
Zum Zeitpunkt t = 0 ist der Weg null, daher ist die Integrationskonstante C gleich 0. Nun setzt man noch die beiden Integrationsgrenzen 16 und 0 ein:
$$s(16) = \frac{5}{8}⋅16^2 + 10⋅16 =320\ m$$
Berechnung der Größen durch Differenzieren – prinzipielle Vorgehensweise
Für die Berechnung der Momentangeschwindigkeit und der Beschleunigung
durch Differenzieren gibt es auch ein praktisches Beispiel weiter unten!
Link zu Unterseite
- Zu den Ableitungen gibt es eine eigene Seite: Differenzieren: Ableitungsregeln & Beispiele.
Die Geschwindigkeit v(t) ist die Ableitung des Weges s(t) nach der Zeit t, siehe dazu auch “Berechnung der Momentangeschwindigkeit” weiter unten:
$$\vec v(t)=\dot{\vec s} (t)=\frac{d}{dt}\vec s(t)$$
Die Beschleunigung a(t) ist die erste Ableitung der Geschwindigkeit v(t) bzw. die zweite Ableitung des Weges s(t) nach der Zeit t:
$$\vec a(t) = \dot{\vec v}(t)=\frac{d}{dt}\vec v(t)=\ddot{\vec s}(t)=\frac{d^2}{d^2t}\vec s(t)$$
Die SI-Einheit des Ruckes ist m/s³. Den Ruck j(t) berechnet man wie folgt:
$$\vec j(t) = \dot{\vec a}(t)=\frac{d}{dt}\vec a(t)=\ddot{\vec v}(t)=\frac{d^2}{d^2t}\vec v(t)=\dddot{\vec s}(t)=\frac{d^3}{d^3t}\vec s(t)$$
Durchschnitts- & Momentangeschwindigkeit
Für die Berechnung der Durchschnitts- und Momentan-Geschwindigkeit gibt es auch ein praktisches Beispiel!
Durchschnittsgeschwindigkeit (Differenzenquotient)
Die Durchschnittsgeschwindigkeit v im Intervall [t0; t1] – auch mittlere Geschwindigkeit genannt – wird mit dem Differenzenquotienten bestimmt:
$$\overline{v}=\frac{\Delta s}{\Delta t}=\frac{s(t_1)-s(t_0)}{t_1-t_0}=k=\frac{zurückgelegter\ Weg}{benötigte\ Zeit}$$
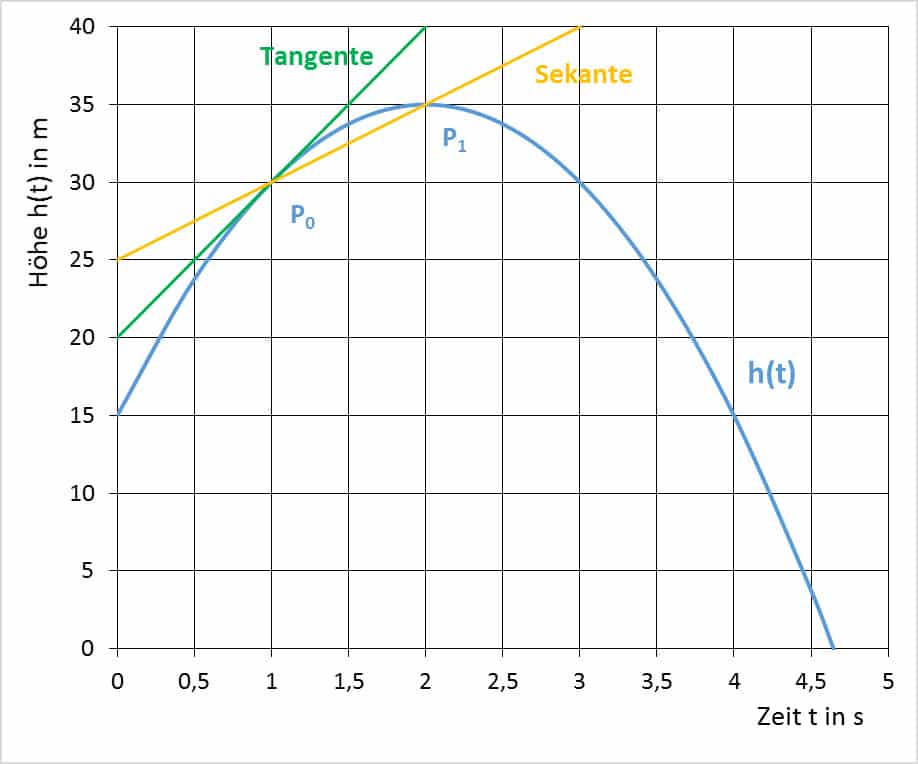
Der Differenzenquotient entspricht der Steigung k der Sekante (gelbe Linie), vgl. Abbildung 4.
Momentangeschwindigkeit (Differentialquotient – 1. Ableitung)
Die momentane Geschwindigkeit v zum Zeitpunkt t0 (auch als momentane Änderungsrate bezeichnet) wird mit dem Differentialquotienten ermittelt, der der Grenzwert (= Limes) des Differenzenquotienten ist:
$$v(t)=\lim \limits_{t_1 \to t_0} \frac{s(t_1)-s(t_0)}{t_1-t_0}$$
Einfacher ist es jedoch, die Momentangeschwindigkeit mit Hilfe der 1. Ableitung des Weges nach der Zeit t zu berechnen:
$$v(t)=\frac{d}{dt}s(t)=\dot s(t)$$
Um die Momentangeschwindigkeit zu bekommen, setzt man für t den Wert t0 ein. Der Differentialquotient bzw. die erste Ableitung des Weges nach der Zeit t entspricht der Steigung k der Tangente (grüne Linie) zum Zeitpunkt t0, vgl. Abbildung 4 weiter unten.
Beispiel: Berechnung des Differentialquotienten mit dem Limes
Es sei die Funktion h(t) aus dem folgenden Beispiel gegeben:
$$h(t) = s(t) = -5⋅t^2 + 20⋅t + 15$$
Einsetzen dieser Funktion in den Differentialquotienten und passend herausheben ergibt:
$$v(t)=\lim \limits_{t_1 \to t_0} \frac{s(t_1)-s(t_0)}{t_1-t_0}=\lim \limits_{t_1 \to t_0}\frac{-5·t_1^2+20·t_1+15-(-5·t_0^2+20·t_0+15)}{t_1-t_0}$$
$$=\lim \limits_{t_1 \to t_0}\frac{-5·t_1^2+20·t_1+15+5·t_0^2-20·t_0-15)}{t_1-t_0}$$
$$=\lim \limits_{t_1 \to t_0}\frac{-5·(t_1^2-t_0^2)+20·(t_1-t_0)+15-15}{t_1-t_0}$$
Unter Anwendung des Binomischen Lehrsatzes und mit Kürzen erhält man:
$$=\lim \limits_{t_1 \to t_0}\frac{-5·(t_1-t_0)·(t_1+t_0)+20·(t_1-t_0)}{t_1-t_0}=\lim \limits_{t_1 \to t_0}(-5·(t_1+t_0)+20)$$
Nun lässt man t1 gegen t0 gehen:
$$=-5·(t_0+t_0)+20=-5·2·t_0+20=-10·t_0+20$$
Wie man sieht, ist differenzieren wesentlich einfacher und auch schneller!
Ausführliches Beispiel aus der Praxis
Angabe
Eine Kugel oder ein Ball wird zum Zeitpunkt t = 0 s von einem Turm senkrecht in die Höhe geschossen (lotrechter Wurf nach oben). Die Funktionsgleichung für die Höhe über Grund in Abhängigkeit von der Zeit lautet:
$$h(t) = -10/2⋅t^2 + 20⋅t + 15$$
a) Wie hoch ist der Turm?
b) Wie groß ist die Abschussgeschwindigkeit? Gib die Geschwindigkeit auch in km/h an!
c) Wann hat die Kugel die größte Höhe erreicht und wie hoch ist sie dann?
d) Berechne die Momentangeschwindigkeit zum Zeitpunkt t = 1 und die Gleichung der Tangente!
e) Ermittle die Durchschnittsgeschwindigkeit im Intervall [1; 2] und die Gleichung der Sekante!
f) Wann und mit welcher Geschwindigkeit trifft sie auf dem Boden auf?
g) Bestimme die Beschleunigung in Abhängigkeit von t!
h) Zeichne h(t), v(t) und a(t).
Hier geht’s direkt zu den Lösungen: a), b), c), d), e), f), g), h)
Wie man auf die Funktion h(t) der Angabe kommen kann, wird weiter oben erklärt.
Lösungen der Aufgabe
Antwort a)
Um die Höhe des Turmes zu bestimmen, muss man in der Funktionsgleichung h(t) t gleich Null setzen:
$$h(0) = – 10/2⋅0^2 + 20⋅0 + 15$$
Die ersten beiden Terme fallen weg, somit erhält man: h(0) = 15. Der Turm ist also 15 m hoch.
Antwort b)
Um die Momentangeschwindigkeit zu erhalten, muss man h(t) einmal nach t ableiten:
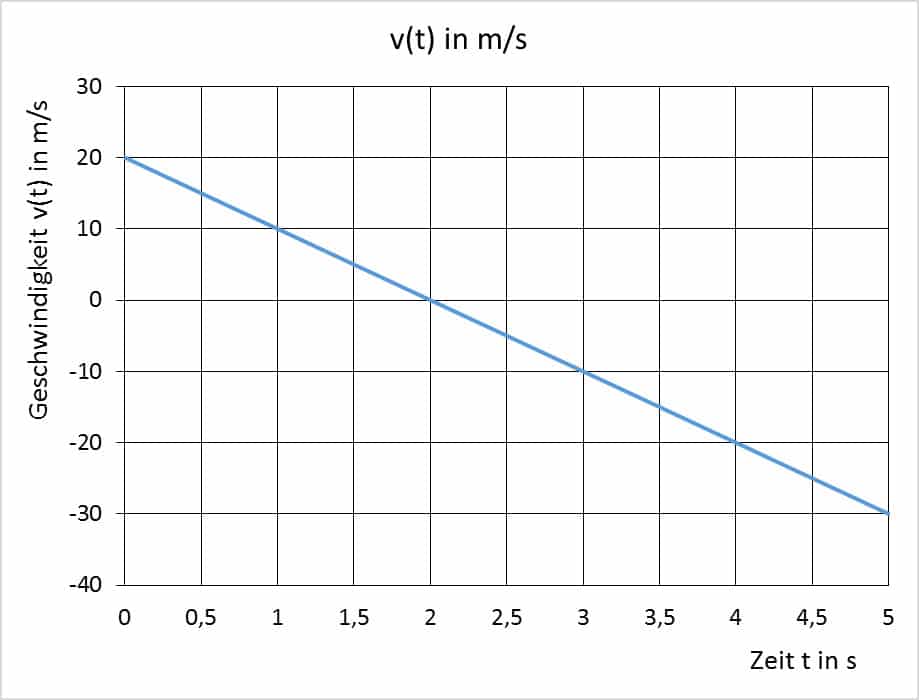
$$v(t) = – 10⋅t + 20$$
Zum Zeitpunkt des Abschusses ist t gleich 0, also erhält man:
$$v(0) = – 10⋅0 + 20 = 20\ \frac{m}{s}$$
Um km/h zu erhalten, multipliziert man die Geschwindigkeit in m/s einfach mit 3.6: 20⋅3.6 = 72 km/h.
Antwort c)
Die größte Höhe hat die Kugel dann erreicht, wenn die Geschwindigkeit null wird. Also:
$$v(t) = 0 = – 10⋅t + 20$$
Durch Umformen erhält man: t = 2 s.
Andere Überlegung: Die größte Höhe muss ein Extremwert (“Hochpunkt”) der Funktion h(t) sein. Extremwerte werden berechnet, indem man die erste Ableitung der Funktion bildet und diese gleich null setzt, da hier die Tangente waagrecht verläuft und somit die Steigung 0 sein muss, siehe auch Steigung der Tangente:
$$h'(t) = v(t) = 0 = – 10⋅t + 20$$
Um die gesuchte Höhe zu erhalten, setzt man für t den eben ermittelten Wert ein:
$$h(2) = – \frac{10}{2}⋅2^2 + 20⋅2 + 15 = 35\ m$$
Antwort d)
Die Momentangeschwindigkeit wurde schon unter b) berechnet. Um die Geschwindigkeit zum Zeitpunkt t = 2 zu erhalten, setzt man t gleich 1:
$$v(1) = – 10⋅1 + 20 = 10\ m/s$$
Die Gleichung einer Geraden lautet allgemein: f(x) = y = k⋅x + d. Im vorliegenden Fall wird x durch t ersetzt:
$$f(t) = y = k⋅t + d$$
Die Steigung ist bekannt, sie entspricht der eben berechneten Geschwindigkeit: k = 10. Die t-Koordinate ist 1, den y-Wert erhält man, indem man 1 für t in h(t) einsetzt:
$$h(1) = – 10/2⋅1^2 + 20⋅1 + 15 = y = 30$$
Somit lautet die Geradengleichung: 30 = 10⋅1 + d. Durch Umformen ergibt sich d = 20. Nun setzt man in y = k⋅t + d die ermittelten Werte für k und d ein und erhält damit die gesuchte Tangentengleichung:
$$y = 10⋅t + 20$$
Antwort e)
Die Durchschnittsgeschwindigkeit v im Intervall [1; 2], die der Steigung k der Sekante entspricht, wird mit dem Differenzenquotienten ermittelt. Den Wert h(t1) = h(2) = 35 kennt man schon aus Antwort c), h(t0) = h(1) muss noch bestimmt werden, indem man für t die Zahl 1 in h(t) einsetzt:
$$h(1) = – \frac{10}{2}⋅1^2 + 20⋅1 + 15 = 30\ m$$
Mit den nun erhaltenen Werten kann der Differenzenquotient berechnet werden:
$$\overline{v}=\frac{\Delta s}{\Delta t}=\frac{h(t_1)-h(t_0)}{t_1-t_0}=\frac{35-30}{2-1}=\frac{5}{1}=5\ \frac{m}{s}$$
Die Gleichung der Sekante bestimmt man ähnlich wie in d). In die allgemeine Geradengleichung setzt man einen Punkt und die soeben berechnete Steigung k (≙ dem Differenzenquotienten) ein:
$$f(2) = 35 = 5⋅2 + d$$
Formt man dies um, erhält man d = 25 und damit die Sekantengleichung:
$$y = 5⋅t + 25$$
Antwort f)
Die Kugel trifft am Boden auf, wenn die Höhe Null ist. Also setzt man h(t) gleich 0:
$$0 = – \frac{10}{2}⋅t^2 + 20⋅t + 15$$
Diese quadratische Gleichung löst man mit der sogenannten kleinen oder großen Lösungsformel bzw. mit dem Taschenrechner. Man erhält:
$$t_{1,2} = 2 ± \sqrt{7}\ s$$
Es ist nur die positive Lösung gültig, also beträgt t ≈ 4.65 s.
Andere Überlegung: Der Auftreffpunkt muss eine Nullstelle der Funktion h(t) sein. Die Nullstellen werden berechnet, indem man die Funktion h(t) gleich Null setzt.
Die Auftreffgeschwindigkeit bestimmt man, indem man in der Gleichung von der Geschwindigkeit t gleich 4.65 setzt:
$$v(4.65) = – 10⋅4.65 + 20 = – 26.5\ \frac{m}{s}$$
Da die Kugel nicht mehr hinauf-, sondern hinunterfliegt, ist die Geschwindigkeit nun negativ!
Antwort g)
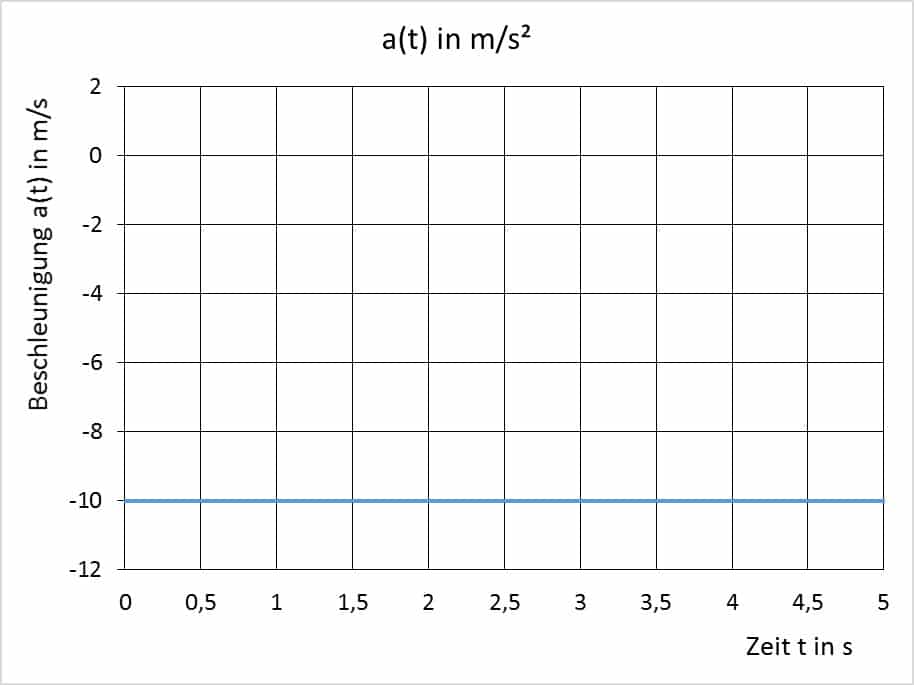
Die Beschleunigung erhält man, indem der Weg zweimal bzw. die Geschwindigkeit einmal nach der Zeit t abgeleitet wird. In diesem Beispiel lautet die Beschleunigung: a(t) = -10 m/s². Die Beschleunigung ist also konstant und nicht mehr von t abhängig, d. h. sie ist zu jedem Zeitpunkt t gleich groß.
Antwort h)
Abbildung 4 zeigt das Weg-Zeit Diagramm, ergänzt mit der Sekante für das Intervall [1; 2] und der Tangente im Punkt P0 (1/30):
In den Abbildungen 5 bzw. 6 sieht man die Geschwindigkeit v in Abhängigkeit von der Zeit t bzw. die konstante Beschleunigung a:
Werbung
Seite erstellt im März 2015. Zuletzt geändert am 13.11.2021.