Auf dieser Seite erfährt man, wie man die Nullstellen, Extremstellen und Wendestellen (bzw. Nullpunkte, Extrempunkte und Wendepunkte) einer Funktion berechnet. Zudem wird gezeigt, welcher grafische Zusammenhang zwischen der Funktionsgleichung f(x), der 1. Ableitung f ´(x) und der 2. Ableitung f ”(x) besteht. Auch weitere wichtige Elemente einer Kurvendiskussion wie Krümmung, Steigung der Tangente und Monotonie werden behandelt. Im Anschluss an die Theorie findet man ein Beispiel.
Inhaltsverzeichnis
Werbung
Übersichtstabelle
Diese Tabelle zeigt, wie man die Nullstellen, Extrempunkte und Wendepunkte einer Funktion f(x) berechnet. Für genauere Informationen sei auf die folgenden Abschnitte verwiesen.
| Nullstellen | Extremstellen | Wendestellen | |
| erforderliche Bedingungen | f(x) = 0 (y-Wert = 0) |
f ´(x) = 0 (Steigung der Tangente = 0) |
f ”(x) = 0 (Krümmung = 0) |
| f ”(x) ≠ 0 | f ”'(x) ≠ 0 | ||
| f ”(x) < 0 ⇒ Hochpunkt H f ”(x) > 0 ⇒ Tiefpunkt T f ”(x) = 0 ⇒ Sattelpunkt S, wenn auch f ”'(x) ≠ 0; kein Extrempunkt!! |
f ´(x) = 0 ⇒ Sattelpunkt S |
||
| Vorzeichen-wechsel | Funktionswert | Steigung der Tangente bzw. Monotonie |
Krümmung |
| f (x) | Funktionsgleichung, y-Wert, Funktionswert |
| f ´(x) | 1. Ableitung der Funktion, Steigung der Tangente an der Stelle x |
| f ”(x) | 2. Ableitung der Funktion, Krümmung der Funktion |
| f ”'(x) | 3. Ableitung der Funktion |
Link zu Unterseite
- Zu den Ableitungen gibt es eine eigene Seite: Differenzieren: Ableitungsregeln & Beispiele.
Hinweis zu Sonderfall:
Sind f(x) = 0, f ´(x) = 0 und f ”(x) = 0 und gilt zudem f ”'(x) ≠ 0, handelt es sich um einen sogenannten Sattelpunkt, der auf der x-Achse liegt: Dieser Punkt ist also ein Wendepunkt mit waagrechter Tangente und zugleich ein Nullpunkt, aber es ist kein Extrempunkt. Wenn auch die x-Koordinate null ist, liegt der Punkt im Ursprung des Koordinatensystems.
Unterschied zwischen Stelle und Punkt
Ein Punkt besitzt in der Ebene stets eine x- und eine y-Koordinate, während mit Stelle nur der x-Wert bezeichnet wird. Den dazugehörenden y-Wert bestimmt man, indem man den x-Wert – also die “Stelle” – in die Funktionsgleichung f(x) einsetzt.
Wichtige Elemente einer Kurvendiskussion
In diesem Kapitel lernt man, was man unter Nullstellen, Extremstellen und Wendestellen einer Funktion versteht und wie man diese Stellen berechnet. Zudem werden grundlegende Begriffe wie Krümmung und Monotonie erklärt.
Zunächst betrachte man den Graphen einer sogenannten Polynomfunktion dritten Grades mit folgender Funktionsgleichung:
$$f(x)=\frac{1}{54}·x^3-\frac{1}{18}·x^2-\frac{4}{9}·x+\frac{40}{27}$$
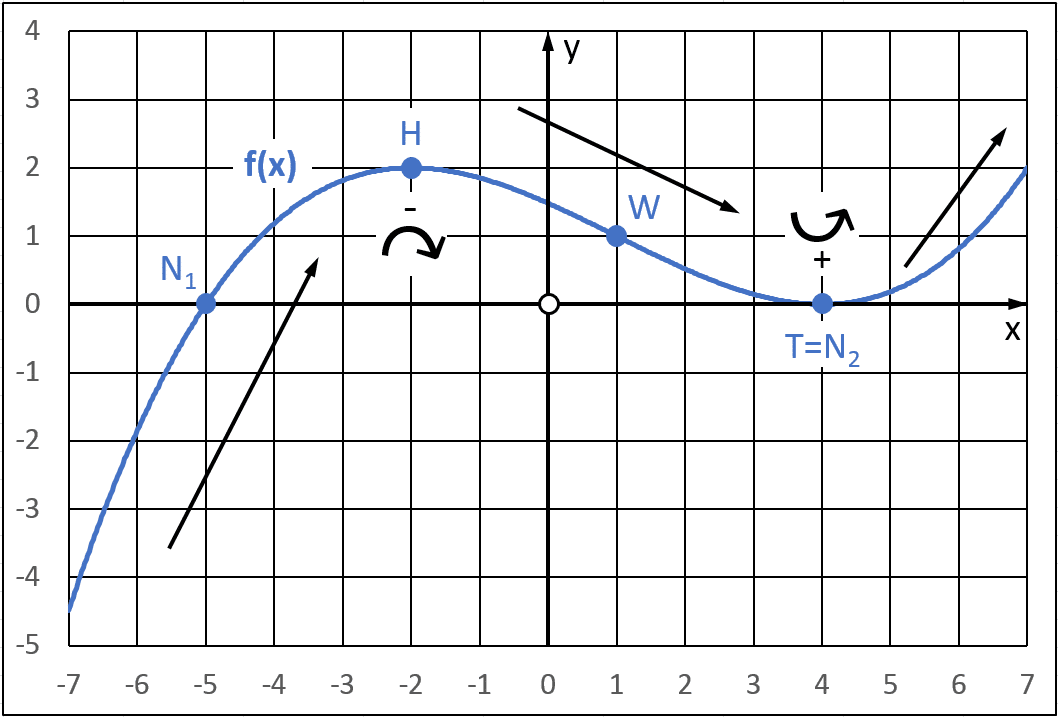
Diese Funktion hat zwei Nullstellen N1 und N2 (= Schnittpunkte mit der x-Achse), zwei Extrempunkte – den Hochpunkt H und den Tiefpunkt T, der zugleich die Nullstelle N2 ist – und einen Wendepunkt W.
Bis zum Hochpunkt H bzw. ab dem Tiefpunkt T ist die Funktion streng monoton steigend, zwischen dem Hochpunkt und dem Tiefpunkt ist sie streng monoton fallend (= Monotonie, dargestellt durch Pfeile).
Die Krümmung links vom Wendepunkt W wird als negativ bzw. rechts gekrümmt bezeichnet (“trauriger Smiley”), rechts vom Wendepunkt ist die Funktion positiv bzw. links gekrümmt (“glücklicher Smiley”).
y-Wert: f(x)
Mit der Funktionsgleichung kann der y-Wert an einer Stelle x bestimmt werden. In den folgenden Abschnitten werden immer nur die Stellen, d. h. die x-Koordinaten eines speziellen Punktes, berechnet. Will man hingegen die Punkte ermitteln, muss die jeweilige Stelle noch in die Funktionsgleichung f(x) eingesetzt werden. Als Ergebnis erhält man die y-Werte der gesuchten Punkte.
Steigung der Tangente: f ´(x) & Monotonie
Die Steigung der Tangente an einer beliebigen Stelle x der Funktion berechnet man durch einmal Ableiten der Funktionsgleichung – man bildet also f ´(x):
| f ´(x) < 0 | f ´(x) = 0 | f ´(x) > 0 |
| ↘ | → | ↗ |
| negative Steigung der Tangente |
keine Steigung, waagrechte Tangente |
positive Steigung der Tangente |
Das Vorzeichen der Steigung der Tangente ändert sich in den Extremstellen, die waagrechte Tangenten besitzen – d. h., die Steigung der Tangenten ist dort 0.
Auch die Monotonie ändert sich in den Extremstellen: Vor einem Hochpunkt bzw. nach einem Tiefpunkt ist die Funktion streng monoton steigend, nach einem Hochpunkt bzw. vor einem Tiefpunkt ist sie hingegen streng monoton fallend, vgl. auch obige Grafik. In einem Sattelpunkt bleibt die Monotonie erhalten, da es sich hierbei um keine Extremstelle handelt.
| f ´(x) > 0 | f ´(x) = 0 | f ´(x) < 0 | f ´(x) = 0 | f ´(x) > 0 |
| ↗ | → | ↘ | → | ↗ |
| positive Steigung der Tangente |
keine Steigung, Hochpunkt H |
negative Steigung der Tangente |
keine Steigung, Tiefpunkt T |
positive Steigung der Tangente |
| streng monoton steigend | streng monoton fallend | streng monoton steigend |
Krümmung: f ”(x)
Die Krümmung einer Funktion berechnet man durch zweimaliges Ableiten der Funktionsgleichung – man bildet also f ”(x). Es gibt drei Möglichkeiten, wie eine Funktion an der Stelle x gekrümmt sein kann, wobei dafür mehrere Bezeichnungen üblich sind:
| f ”(x) < 0 | f ”(x) = 0 | f ”(x) > 0 |
| ↷ | ↺ | |
| – rechts gekrümmt – negativ gekrümmt – konkav |
nicht gekrümmt | – links gekrümmt – positiv gekrümmt – konvex |
| “trauriger Smiley” | “glücklicher Smiley” |
Das Vorzeichen der Krümmung ändert sich in den Wendestellen; dort ist die Krümmung null.
Schnittpunkt mit der y-Achse
Die y-Koordinate des Schnittpunkts einer Funktion mit der y-Achse berechnet man, indem man in der Funktionsgleichung x gleich 0 setzt. Es kann immer nur maximal einen Schnittpunkt mit der y-Achse geben, da es sich sonst um keine Funktion handeln würde: Jeder Stelle x darf nur genau ein y-Wert entsprechen. Die Umkehrung gilt jedoch nicht, da einem y-Wert sehr wohl mehrere x-Werte zugeordnet sein können.
Nullstellen (Schnittpunkte mit der x-Achse)
Eine Nullstelle ist die x-Koordinate jenes Punktes der Funktion, dessen y-Wert Null ist. Nullpunkte sind also die Schnittpunkte der Funktion mit der x-Achse und werden üblicherweise mit N bezeichnet. In einer Nullstelle ändern sich die Vorzeichen der Funktionswerte. Die Nullstellen einer Funktion bekommt man, indem man die Funktionsgleichung f(x) null setzt und anschließend aus dieser Gleichung x berechnet:
$$f(x)=0$$
Extremstellen (lokales Extremum)
In den Extremstellen ändert sich das Vorzeichen der Steigung der Tangente. In der Extremstelle selbst ist die Steigung 0, das heißt, die Tangente verläuft hier waagrecht. Daher berechnet man die Extremstellen einer Funktion durch Nullsetzen der 1. Ableitung f´(x) und anschließendem Lösen dieser Gleichung nach x:
$$f'(x)=0$$
Zusätzlich darf die Krümmung nicht Null sein, also muss gelten:
$$f^{“}(x)≠0$$
Bei Extremstellen handelt es sich um lokale Extrema. Ob ein Hochpunkt oder ein Tiefpunkt vorliegt, kann man mithilfe der 2. Ableitung bestimmen. Meist wird ein Hochpunkt mit H und ein Tiefpunkt mit T bezeichnet.
| f ”(x) < 0 | f ”(x) = 0 | f ”(x) > 0 |
| lokales Maximum Hochpunkt H |
Sattelpunkt S, wenn f ”'(x) ≠ 0; kein Extrempunkt! |
lokales Minimum Tiefpunkt T |
| negative Krümmung | keine Krümmung | positive Krümmung |
Wenn es sich um eine Extremstelle handelt, muss f ”(x) ≠ 0 sein. Ist die 2. Ableitung jedoch gleich 0 und gilt zudem f ”'(x) ≠ 0, handelt es sich um keine Extremstelle, sondern um einen Sattelpunkt. Ein Sattelpunkt ist ein Wendepunkt mit waagrechter Tangente.
Wendestellen
Wendepunkte werden fast immer mit W abgekürzt. In den Wendestellen ändert sich das Vorzeichen der Krümmung, in den Wendestellen selbst ist die Krümmung 0. Daher berechnet man die Wendestellen einer Funktion durch Nullsetzen der 2. Ableitung f ”(x) und anschließendem Lösen dieser Gleichung nach x:
$$f^{“}(x)=0$$
Zusätzlich muss folgende Bedingung erfüllt sein:
$$f^{“‘}(x)≠0$$
Spezialfall: Sattelpunkt
Ein Sattelpunkt – oder auch Terrassenpunkt genannt – ist ein Wendepunkt mit waagrechter Tangente. Für einen Sattelpunkt muss daher noch folgende Bedingung gelten:
$$f'(x)=0$$
Werbung
Anzahl der Nullstellen / Extremstellen / Wendestellen bei Polynomfunktionen
Eine Polynomfunktion kann maximal
- n Nullstellen
- n-1 Extremstellen
- und n-2 Wendestellen
haben, wobei n den Grad der Polynomfunktion angibt. Der Grad entspricht der größten Hochzahl von x.
Eine ungerade Polynomfunktion muss mindestens eine Nullstelle besitzen. Gerade Polynomfunktionen können auch gar keine Nullstelle haben, sie besitzen jedoch immer zumindest eine Extremstelle.
Graphen verschiedener Polynomfunktionen
Es folgen Graphen von 4 verschiedenen Polynomfunktionen 3. Grades, also in der Form f(x) = a·x3 + b·x2 + c·x + d, wobei sich die Anzahl der Nullstellen und Extremstellen durch Variation der Parameter a, b, c und d verändert. Außerdem werden Graphen einer Polynomfunktion 2. Grades und einer Polynomfunktion 4. Grades gezeigt:
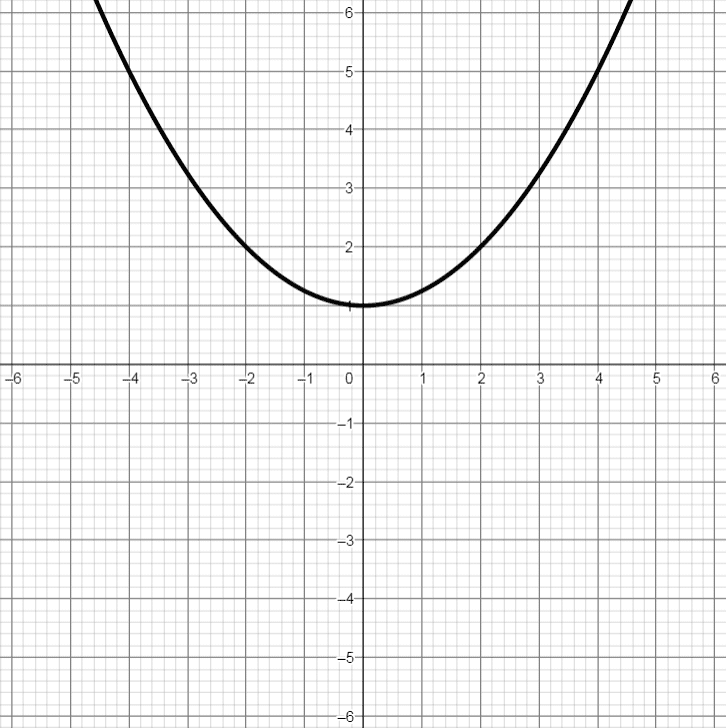
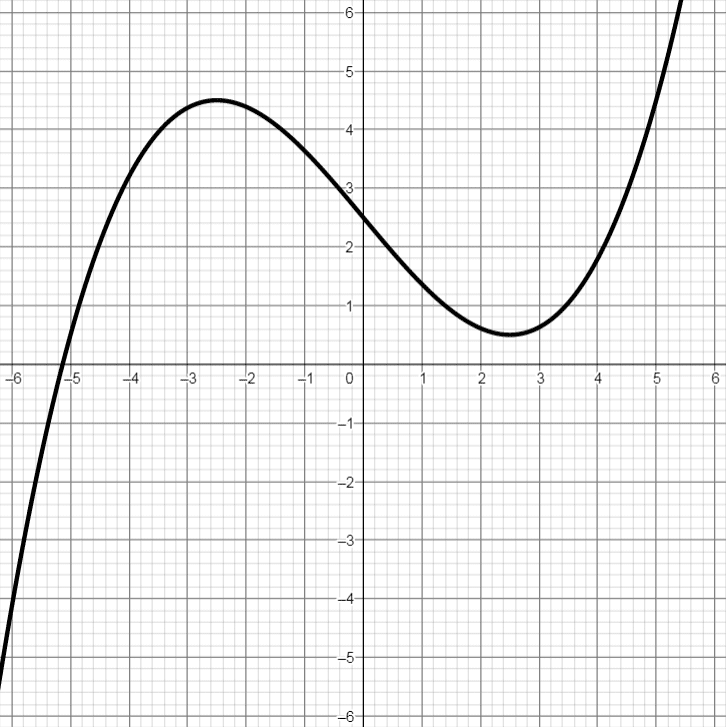
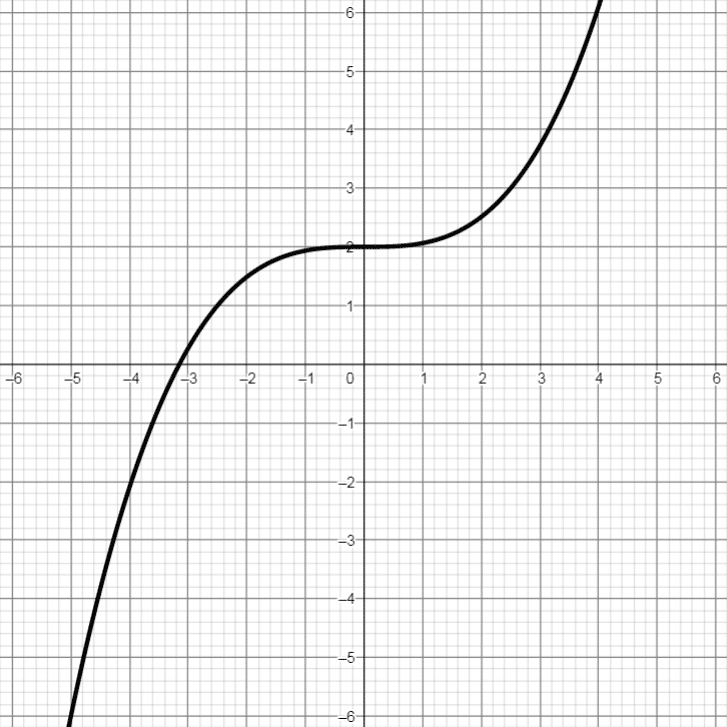
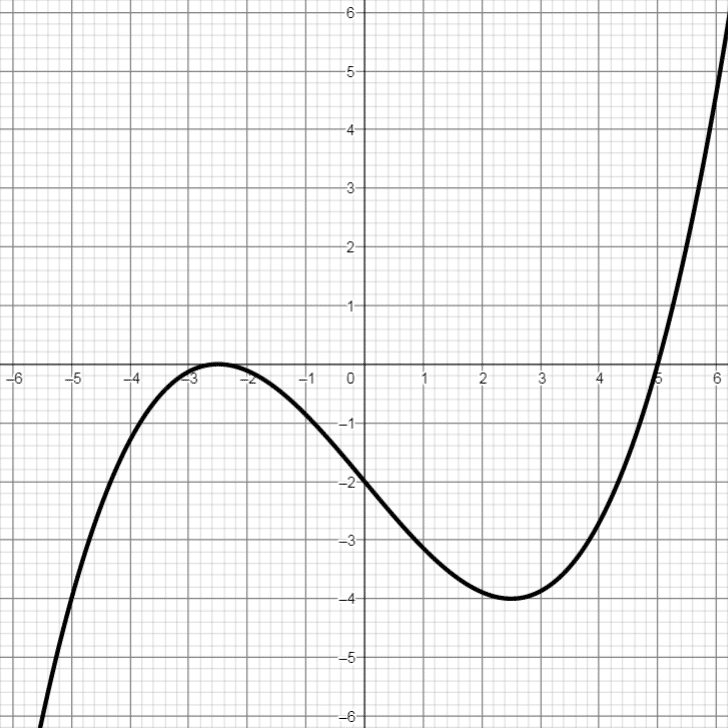
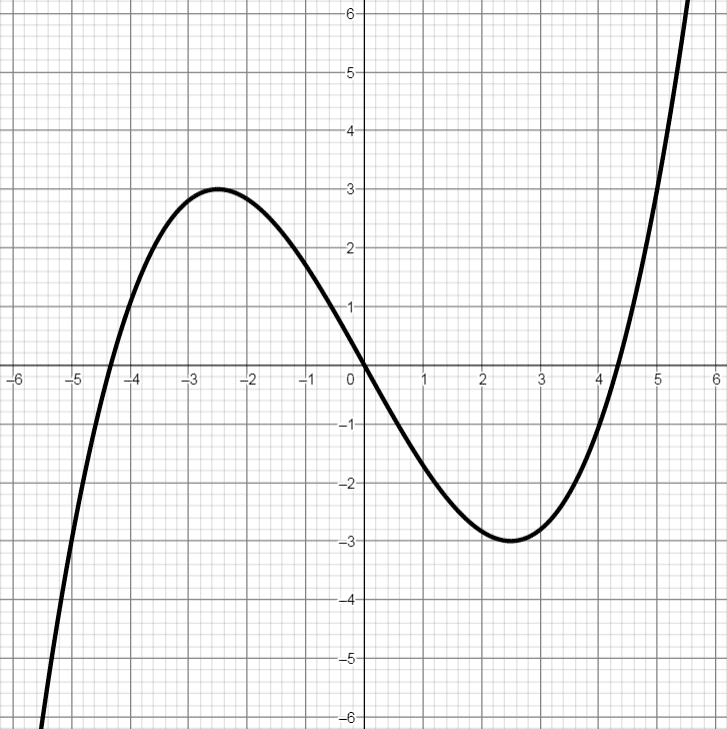
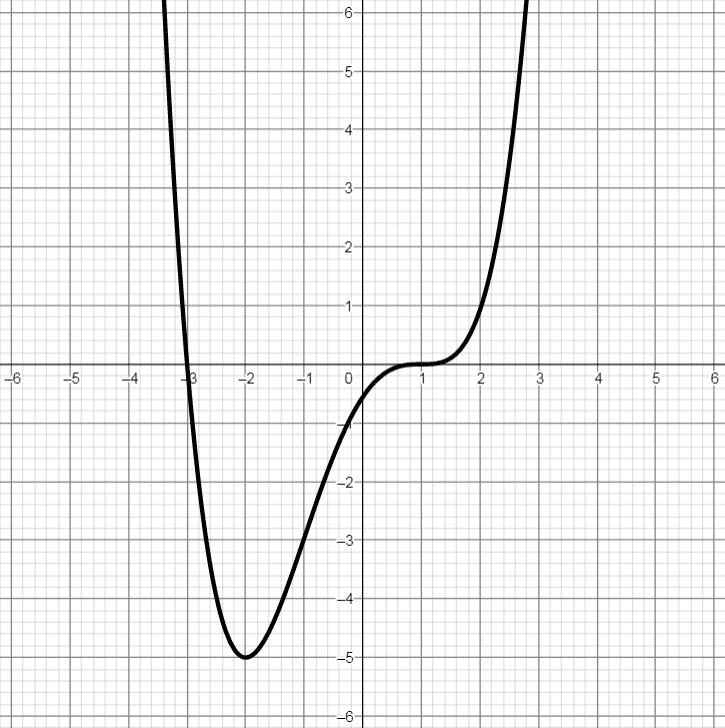
* Dieser Graph wird im Anschluss als Beispiel durchgerechnet!
Grafischer Zusammenhang zwischen f(x), f ´(x) & f ”(x)
Den grafischen Zusammenhang zwischen der Funktion f(x), der 1. Ableitung f ´(x) und der 2. Ableitung f ”(x) zeigt die folgende Abbildung:
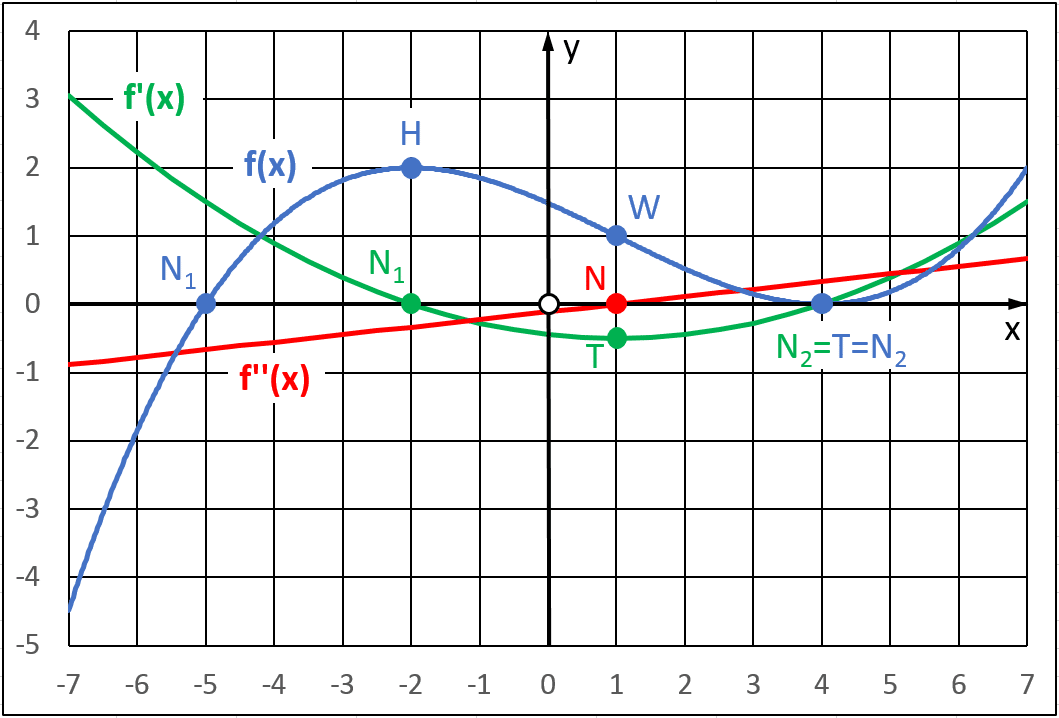
Extremstellen H und T
Die beiden Extremstellen H und T der Funktion f(x) werden zu den Nullstellen N1 und N2 der 1. Ableitung f ´(x), wobei T und N2 zusammenfallen, da die Extremstelle T zugleich die Nullstelle N2 von f(x) ist.
Kontrolle der erforderlichen Bedingungen für Hochpunkt H:
Liest man aus dem obigen Diagramm die Funktionswerte an der Stelle x = -2 ab, kann man überprüfen, ob die erforderlichen Bedingungen für den Hochpunkt H eingehalten werden. Der Funktionswert der 1. Ableitungsfunktion und somit die Steigung der Tangente ist wie gefordert null: f ´(-2) = 0. Der Funktionswert der 2. Ableitung ist ungleich Null: f ”(-2) = -0.33. Da dieser Wert kleiner als 0 ist und folglich die Krümmung an dieser Stelle negativ ist, muss es sich bei dieser Extremstelle um einen Hochpunkt handeln.
Wendestelle W
Die Wendestelle W von der Funktion f(x) wird zur Extremstelle T der 1. Ableitung f ´(x) bzw. zur Nullstelle N der 2. Ableitung f ”(x), diese drei Punkte liegen also genau übereinander.
Beispiel: Berechnung Nullpunkte, Extrempunkte, Wendepunkte – Kurvendiskussion
Es ist folgende Polynomfunktion 4. Grades gegeben:
$$f(x)=\frac{5}{27}·x^4-\frac{10}{9}·x^2+\frac{40}{27}·x-\frac{5}{9}$$
Aufgabe:
Es ist eine (unvollständige) Kurvendiskussion durchzuführen:
- Berechnung der Nullpunkte, Extrempunkte, Wendepunkte, Schnittpunkt mit der y-Achse und der Gleichungen der Wendetangenten.
- Grafische Darstellung der Funktion, der 1. und 2. Ableitung, aller berechneten Punkte und der Wendetangenten.
Berechnung der Nullpunkte
Für die Berechnung der Nullstellen muss man f(x) gleich null setzen:
$$f(x)=0\Rightarrow0=\frac{5}{27}·x^4-\frac{10}{9}·x^2+\frac{40}{27}·x-\frac{5}{9}$$
Die Lösungen dieser Gleichung erhält man z. B. mit einem geeigneten Taschenrechner oder GeoGebra. Man bekommt:
$$x_1=-3\qquad x_2=1\qquad \Rightarrow N_1(-3|0)\qquad N_2(1|0)$$
Berechnung der Extrempunkte
Zunächst bildet man die 1. Ableitung und setzt diese anschließend gleich null:
$$f'(x)=\frac{20}{27}·x^3-\frac{20}{9}·x+\frac{40}{27}\Rightarrow 0=\frac{20}{27}·x^3-\frac{20}{9}·x+\frac{40}{27}$$
Als Lösung für diese Gleichung erhält man:
$$x_1=-2\qquad x_2=1$$
Nun muss mithilfe der 2. Ableitung (= Krümmung) festgestellt werden, um welche Art von Extremstelle es sich jeweils handelt bzw. ob überhaupt eine Extremstelle vorliegt. Die 2. Ableitung der Funktion lautet:
$$f^{“}(x)=\frac{60}{27}·x^2-\frac{20}{9}$$
In diese Gleichung setzt man für x die beiden Extremstellen -2 und 1 ein:
$$f^{“}(-2)=\frac{60}{27}·(-2)^2-\frac{20}{9}=\frac{20}{3}>0\Rightarrow Tiefpunkt$$
$$f^{“}(1)=\frac{60}{27}·1^2-\frac{20}{9}=0\Rightarrow Sattelpunkt?$$
Bei der ersten Extremstelle handelt es sich um einen Tiefpunkt, da die Krümmung positiv ist. In der 2. Extremstelle ist die Krümmung gleich 0, also kann das keine Extremstelle sein. Es liegt wahrscheinlich ein Sattelpunkt vor. Ob diese Annahme zutrifft wird im nächsten Abschnitt überprüft. Durch Einsetzen von x = -2 in f(x) bekommt man die y-Koordinate des Tiefpunkts T:
$$f(-2)=\frac{5}{27}·(-2)^4-\frac{10}{9}·(-2)^2+\frac{40}{9}·(-2)-\frac{5}{9}=-5$$
$$\Rightarrow T(-2|-5)$$Berechnung der Wendepunkte
Zur Berechnung der Wendestellen muss man als Erstes die schon zuvor gebildete 2. Ableitung 0 setzen und aus dieser Gleichung x berechnen:
$$0=\frac{60}{27}·x^2-\frac{20}{9}\qquad \Rightarrow x_1=-1\qquad x_2=1$$
Nun muss man mit Hilfe der 3. Ableitung prüfen, ob es sich bei diesen beiden Lösungen tatsächlich um Wendestellen handelt:
$$f^{“‘}(x)=\frac{40}{9}·x$$
$$f^{“‘}(-1)=-\frac{40}{9}≠0\qquad f^{“‘}(1)=\frac{40}{9}≠0\qquad \Rightarrow Wendestellen$$
Beide Lösungen sind Wendestellen, wobei die 2. Wendestelle eine waagrechte Tangente besitzt und es sich somit tatsächlich um einen Sattelpunkt handelt, vgl. vorigen Abschnitt. Einsetzen dieser Werte in die Funktionsgleichung ergibt:
$$f(-1)=\frac{5}{27}·(-1)^4-\frac{10}{9}·(-1)^2+\frac{40}{27}·(-1)-\frac{5}{9}=-\frac{80}{27}$$
$$\Rightarrow W_1\left(-1\bigg| -\frac{80}{27}\right)$$
$$f(1)=\frac{5}{27}·1^4-\frac{10}{9}·1^2+\frac{40}{27}·1-\frac{5}{9}=0\qquad \Rightarrow W_2=S(1|0)$$
Berechnung des Schnittpunkts mit der y-Achse
Dazu setzt man in der Funktionsgleichung x = 0:
$$f(0)=\frac{5}{27}·0^4-\frac{10}{9}·0^2+\frac{40}{27}·0-\frac{5}{9}=-\frac{5}{9}\qquad \Rightarrow P\left(0\bigg|-\frac{5}{9}\right)$$
Gleichungen der Wendetangenten
Bei den Gleichungen der Wendetangenten handelt es sich um Geraden der Form y = k·x + d. Die Steigung k bekommt man mit der 1. Ableitung, indem man für x die jeweilige Wendestelle einsetzt. Die Steigung der Tangente im 1. Wendepunkt beträgt:
$$f'(-1)=\frac{20}{27}·(-1)^3-\frac{20}{9}·(-1)+\frac{40}{27}=\frac{80}{27}\qquad \Rightarrow k=\frac{80}{27}$$
Die Wendetangente muss natürlich durch den Wendepunkt verlaufen, daher setzt man die Koordinaten des Wendepunkts in die allgemeine Geradengleichung für x und y ein. Die Steigung k wurde soeben berechnet. Durch Umformen bekommt man d und somit auch die gesuchte Gleichung der Wendetangente:
$$y=k·x+d\Rightarrow -\frac{80}{27}=\frac{80}{27}·(-1)+d\Rightarrow d=0\Rightarrow y=\frac{80}{27}·x$$
Der 2. Wendepunkt ist bekanntlich ein Sattelpunkt. Sattelpunkte besitzen waagrechte Tangenten, das heißt, die Steigung k ist in diesem Fall 0. Der Sattelpunkt fällt zudem mit der Nullstelle N2 zusammen, also entspricht die x-Achse der Tangente im Sattelpunkt. Die Gleichung lautet:
$$y=0$$
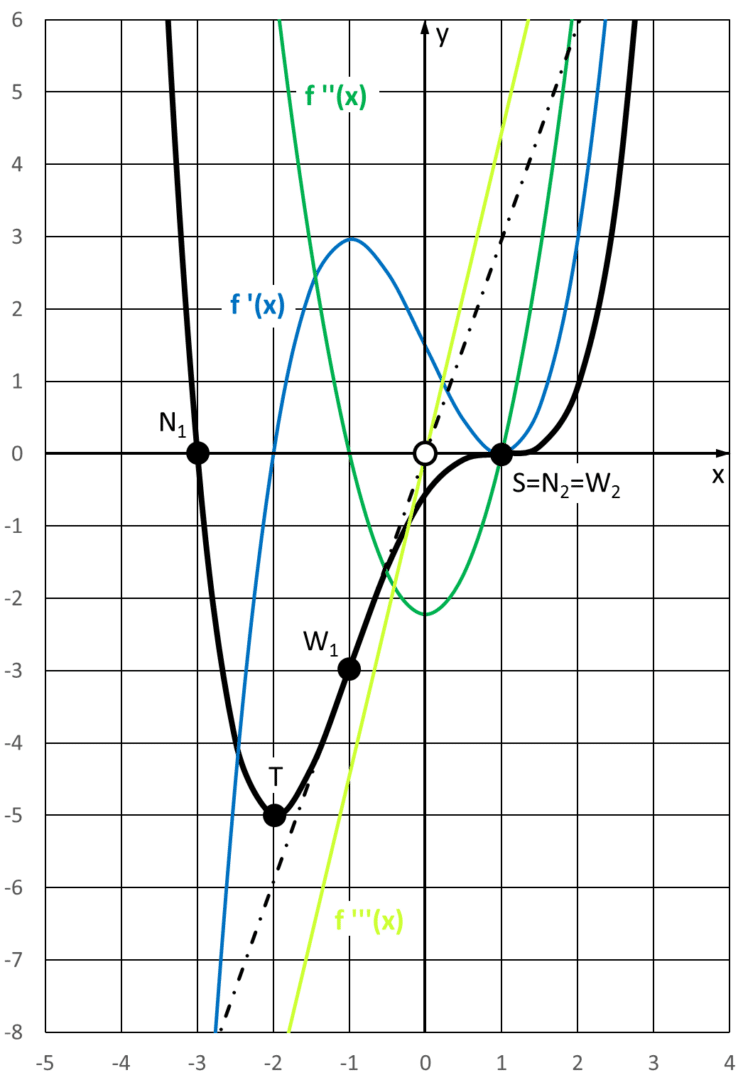
Funktionsgraph mit den drei Ableitungen & Wendetangenten
In der nebenstehenden bzw. nächsten Abbildung ist Folgendes zu sehen:
- Funktion f(x) – in schwarz
- 1. Ableitung f ´(x) – in blau
- 2. Ableitung f ”(x) – in grün
- 3. Ableitung f ”'(x) – in gelb
- Nullpunkte N1 und N2
- Tiefpunkt T
- Wendepunkte W1 und W2 (= Sattelpunkt S)
- Tangente durch W1 – schwarz strichliert
Interessant ist, dass N2 und W2 zusammenfallen. Dieser Punkt ist der Sattelpunkt S, er ist zudem ein Nullpunkt und Extrempunkt von f ´(x) und ein Nullpunkt von f ”(x).
Werbung
Seite erstellt am 31.05.2019. Zuletzt geändert am 01.05.2022.