Mit diesem Online-Rechner kannst du lineare Prozesse (Wachstum und Abnahme) berechnen und auch die zugrunde liegende Funktionsgleichung ausgeben lassen. Der Graph einer linearen Funktion wird Gerade genannt und wird von diesem Rechner auch dargestellt. Nach dem Rechner findest du Hintergrundinformationen, die vom Rechner verwendeten Formeln und ein Anwendungsbeispiel, bei dem die Gleichung einer Geraden durch zwei Punkte mit diesem Rechner ermittelt wird.
Es ist möglich, entweder
- die Steigung k, die Konstante d, die x-Koordinate des Punktes 1 und die y-Koordinate des Punktes 2
- die Steigung k und die zwei Koordinaten des Punkts 1
- die Konstante d und die beiden Koordinaten des Punkts 1
- oder die beiden Koordinaten der Punkte 1 und 2 einzugeben.
Link zu Unterseite:
Werbung
Rechner für lineare Funktionen & Funktionsgraph
Mit der Voreinstellung wird die Funktionsgleichung ermittelt, wenn die x-Koordinate und die y-Koordinate von zwei Punkten einer Geraden bekannt sind. Es werden also k und d und die Funktionsgleichung berechnet.
Mit xmin und xmax wird der minimale bzw. der maximale Wert auf der x-Achse bestimmt, also der darzustellende Bereich des Funktionsgraphen. Natürlich sind auch negative Eingaben zulässig!
Hinweise
- Bei Auswahl von “Steigung k & Konstante d” können bei Bedarf die x-Koordinate und die y-Koordinate von Punkt 1 bzw. von Punkt 2 eingegeben werden. Die jeweiligen anderen Koordinaten werden berechnet.
- Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular.
Erklärung der Abkürzungen
| k | Steigung der Geraden; ist bei Zunahme positiv, bei Abnahme negativ |
| d | Konstante; entspricht dem Funktionswert bei x = 0: d = f(0) |
Hintergrundwissen & Formeln für lineare Funktionen
Lineare Vorgänge sind recht häufig anzutreffen. Zudem verlaufen oft viele Prozesse zumindest in Teilen linear bzw. können ganz gut linearisiert werden. In der folgenden Aufzählung sind ein paar Beispiele angeführt:
- Ein Kind bekommt monatlich 50 € Taschengeld: Das gesamte Guthaben nach einer beliebigen Anzahl von Monaten kann durch eine lineare Funktion dargestellt werden, falls keine Ausgaben getätigt werden. Die Steigung k beträgt in diesem Fall 50 und die Konstante d wäre 0, wenn das Kind zu Beginn kein Geld besitzt.
- In ein quaderförmiges Becken fließt pro Sekunde 1 Liter Wasser. Beim Wasserstand handelt es sich um einen lineare Zunahme.
Man unterscheidet zwei Arten von linearen Funktionen: homogene und inhomogene lineare Funktionen. Die homogene lineare Funktion ist eine Spezialform der inhomogenen linearen Funktion, bei der die Konstante d null ist. Sie ist auch als direkte Proportionalität bekannt.
Steigung k
Die Steigung k kann sowohl negativ als auch positiv sein. Ist die Steigung negativ, handelt es sich um eine lineare Abnahme. Ist k positiv, spricht man von einer linearen Zunahme. Beträgt die Steigung null, verläuft die Gerade parallel zur x-Achse im Abstand der Konstanten d. Die Steigung k wird mit dem Differenzenquotienten berechnet:
$$k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$$
Es werden zur Berechnung von k also die x- und die y-Koordinaten von zwei verschiedenen Punkten benötigt, die auf der Geraden liegen.
Konstante d
Die Konstante d entspricht dem y-Wert bei x = 0, folglich gilt: d = f(0). Die Gerade schneidet die y-Achse daher im Punkt (0/d). Die Konstante d kann auch null sein. In diesem Fall verläuft die Gerade durch den Ursprung, also durch den Punkt (0/0). Es handelt sich dann um eine homogene lineare Funktion.
Beispiel: Berechnung der Gleichung einer Geraden
Gerade durch zwei Punkte
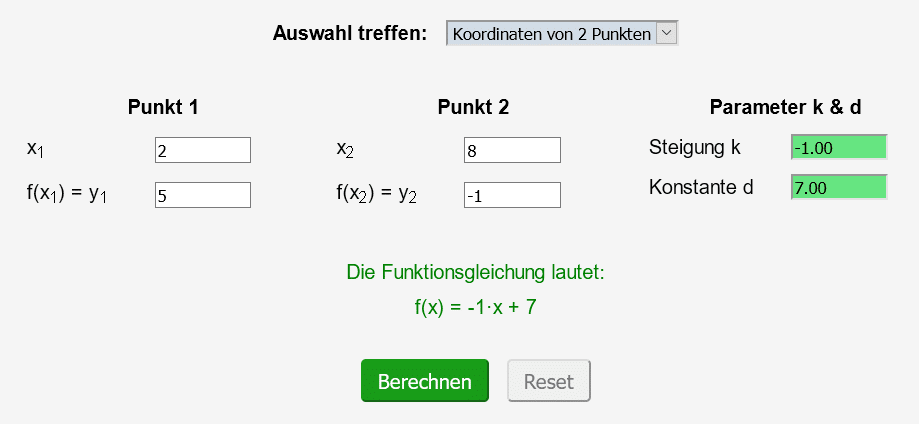
Eine Gerade soll durch die beiden Punkte A (2/5) und B (8/-1) verlaufen. Wie lautet die Funktionsgleichung?
Lösung
Man wählt beim Rechner als Erstes “Koordinaten von 2 Punkten” aus. Dabei handelt es sich um die Voreinstellung. Dann trägt man unter Punkt 1 und Punkt 2 die jeweiligen Koordinaten ein. Den richtig ausgefüllten Rechner zeigt der folgende Screenshot:
Werbung
Seite erstellt am 26.05.2021. Zuletzt geändert am: