This page in English: Cross Sectional Area & Section Modulus (calculator and formulas)
In dieser Formelsammlung finden Sie die Formeln zur Berechnung der axialen und polaren Widerstandsmomente und Flächenträgheitsmomente (auch als Flächenmomente 2. Grades bezeichnet) typischer Stahlprofile. Zudem werden die Formeln zur Berechnung der Torsionsträgheitsmomente und der Torsionswiderstandsmomente dünnwandiger und kreisförmiger Profile angeführt. Im Anschluss wird der rechnerische Zusammenhang zwischen diesen beiden Größen erklärt.
Die Formeln für folgende Querschnitte sind in der Tabelle zu finden:
- Rundstange (Kreis)
- Rundrohr (Kreisring)
- Halb-Rundstab (Halbkreis)
- Rechteck-Profil
- Rechteck-Hohlprofil / Formrohr / Vierkantrohr
- I- bzw. H-Profil (Doppel-T-Träger)
- U- bzw. C-Profil
- T-Profil
- L-Profil (Winkelprofil), gleich- und ungleichschenkelig
- Gleichschenkeliges /gleichseitiges Dreieck
- Sechseck/Sechskant
- Achteck/Achtkant
Links zu Unterseiten:
- Rechner für Flächenträgheitsmomente und Widerstandsmomente
- Balkenrechner (unter anderem Berechnung der Biegespannung)
- Scher- bzw. Schubspannungsrechner
- Herleitung der Formeln zur Berechnung der Flächenträgheitsmomente
Werbung
Formeln für axiale Flächenträgheitsmomente & Widerstandsmomente
Die Einheit für das Flächenträgheitsmoment I ist cm4 oder mm4, für das Widerstandsmoment cm3 oder mm3. Bei der Berechnung von Spannungen bietet sich die Verwendung einer Einheit in mm an, da Spannungen üblicherweise in N/mm2 angegeben werden. In Tabellenbüchern findet man dagegen meist die Einheit cm3 bzw. cm4.
Die Flächenträgheitsmomente werden unter anderem zur Berechnung der Knicksicherheit von Stäben benötigt, die Widerstandsmomente braucht man zur Ermittlung der Spannungen in Trägern bzw. Balken.
Folgende Zusammenhänge gelten für alle Formeln in den Tabellen:
- b3 = B – b
- b4 = B – 2·b
- h3 = H – h
- h4 = H – 2·h
| Querschnittsprofil | Axiale Flächenträgheitsmomente | Widerstandsmomente |
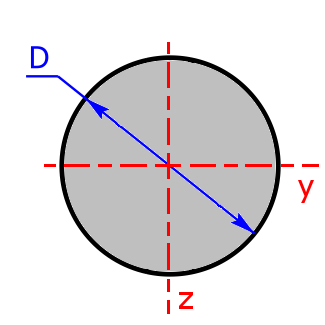 Rundstange (Kreis)
Rundstange (Kreis) |
$$I_y=I_z=\frac{\pi·D^4}{64}$$ | $$W_y=W_z=\frac{\pi·D^3}{32}$$ |
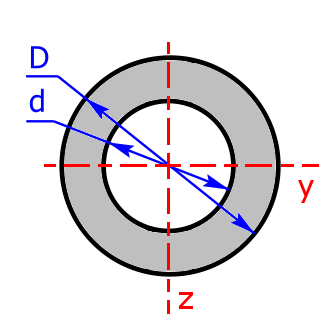 Rundrohr (Kreisring)
Rundrohr (Kreisring) |
$$I_y=I_z=\frac{\pi·(D^4-d^4)}{64}$$ | $$W_y=W_z=\frac{\pi·(D^4-d^4)}{32·D}$$ |
 Quadrat Quadrat |
$$I_y=I_z=\frac{B^4}{12}$$ | $$W_y=W_z=\frac{B^3}{6}$$ |
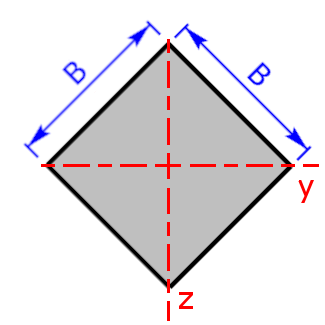 gedrehtes Quadrat |
$$I_y=I_z=\frac{B^4}{12}$$ | $$W_y=W_z=\frac{B^3}{6·\sqrt{2}}$$ $$e_{1,2,3,4}=\frac{\sqrt{2}}{2}·B$$ |
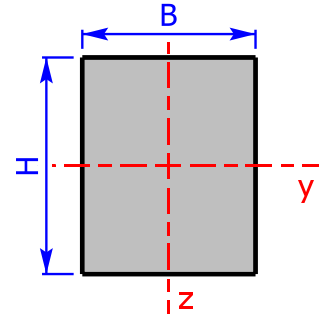 Rechteck-Profil Rechteck-Profil |
$$I_y=\frac{B·H^3}{12}$$ | $$W_y=\frac{B·H^2}{6}$$ |
| $$I_z=\frac{H·B^3}{12}$$ | $$W_y=\frac{H·B^2}{6}$$ | |
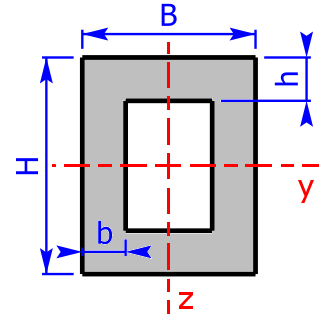 Rechteck- Hohlprofil / Formrohr |
$$I_y=\frac{B·H^3-b_4·(h_4)^3}{12}$$ | $$W_y=\frac{B·H^3-b_4·(h_4)^3}{6·H}$$ |
| $$b_4=B-2·b\qquad h_4=H-2·h\qquad$$ (b4 und h4 = Innenmaße) | ||
| $$I_z=\frac{H·B^3-h_4·(b_4)^3}{12}$$ | $$W_z=\frac{H·B^3-h_4·(b_4)^3}{6·B}$$ | |
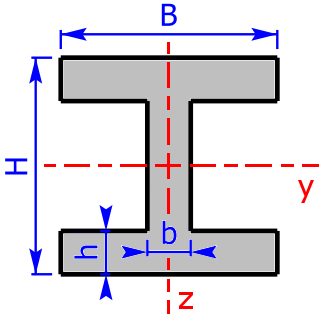 I- bzw. H-Profil |
$$I_y=\frac{B·H^3-b_3·(h_4)^3}{12}$$ | $$W_y=\frac{B·H^3-b_3·(h_4)^3}{6·H}$$ |
| $$b_3=B-b\qquad h_4=H-2·h$$ | ||
| $$I_z=\frac{2·h·B^3+h_4·b^3}{12}$$ | $$W_z=\frac{2·h·B^3+h_4·b^3}{6·B}$$ | |
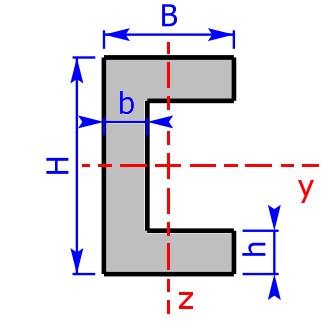 C- bzw. U-Profil $$b_3= B – b$$ $$h_4=H-2·h$$ |
$$I_y=\frac{B·H^3-b_3·(h_4)^3}{12}$$ | $$W_y=\frac{B·H^3-b_3·(h_4)^3}{6·H}$$ |
| $$I_z=\frac{2·h·B^3+h_4·b^3}{3}-(2·h·B+h_4·b)e_3^2$$ | $$W_{{z}_{1,2}}=\frac{I_z}{e_{3,4}}$$ | |
| $$e_3=\frac{1}{2}·\frac{2·h·B^2+h_4·b^2}{2·h·B+h_4·b}$$ | $$e_4=B-e_3$$ | |
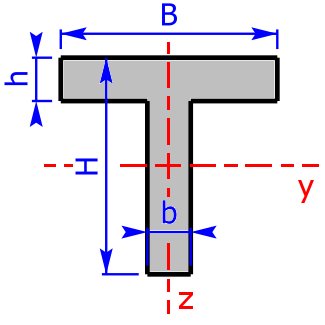 T-Profil $$b_3=B-b$$ $$h_3=H-h$$ |
$$I_y=\frac{b·H^3+b_3·h^3}{3}-(b·H+b_3·h)·e_2^2$$ | $$W_{y_{1,2}}=\frac{I_y}{e_{1,2}}$$ |
| $$e_2=\frac{1}{2}·\frac{b·H^2+b_3·h^2}{b·H+b_3·h}$$ | $$e_1=H-e_2$$ | |
| $$I_z=\frac{h·B^3+h_3·b^3}{12}$$ | $$W_z=\frac{h·B^3+h_3·b^3}{6·B}$$ | |
 L-Profil $$b_3=B-b$$ $$h_3=H-h$$ |
$$I_y=\frac{b·H^3+b_3·h^3}{3}-(b·H+b_3·h)·e_2^2$$ | $$W_{y_{1,2}}=\frac{I_y}{e_{1,2}}$$ |
| $$e_2=\frac{1}{2}·\frac{b·H^2+b_3·h^2}{b·H+b_3·h}$$ | $$e_1=H-e_2$$ | |
| $$I_z=\frac{h·B^3+h_3·b^3}{3}-(h·B+h_3·b)·e_3^2$$ | $$W_{z_{1,2}}=\frac{I_z}{e_{3,4}}$$ | |
| $$e_3=\frac{1}{2}·\frac{h·B^2+h_3·b^2}{h·B+h_3·b}$$ | $$e_4=B-e_3$$ | |
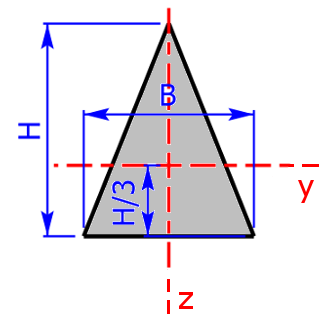 Gleichschenkeliges/ gleichseitiges Dreieck |
$$I_y=\frac{B·H^3}{36}$$ | $$W_{y_1}=\frac{B·H^2}{12}\quad e_1=\frac{H}{3}$$ |
| $$W_{y_2}=\frac{B·H^2}{24}\quad e_2=\frac{2·H}{3}$$ | ||
| $$I_z=\frac{H·B^3}{48}$$ | $$W_{z_{1,2}}=\frac{H·B^2}{24}$$ | |
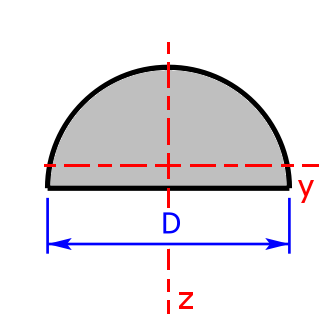 Halbkreis |
$$I_y=0.10976·\left(\frac{D}{2}\right)^4=0.10976·r^4$$ | $$W_{y_1}=0.25861·\left(\frac{D}{2}\right)^3$$ |
| $$W_{y_2}=0.19069·\left(\frac{D}{2}\right)^3$$ | ||
| $$I_z=\frac{1}{2}·\frac{\pi·D^4}{64}=\frac{\pi·D^4}{128}=\frac{\pi·R^4}{8}$$ | $$W_{y_{1,2}}=\frac{1}{2}·\frac{\pi·D^3}{32}=\frac{\pi·D^3}{64}$$ | |
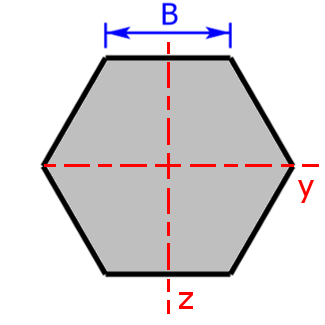 Sechseck/Sechskant |
$$I_y=I_z=\frac{5·\sqrt{3}}{16}·B^4$$ | $$W_y=\frac{5}{8}·B^3$$ |
| $$W_z=\frac{5·\sqrt{3}}{16}·B^3$$ | ||
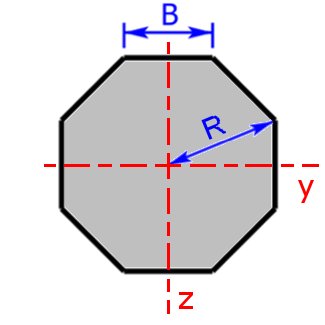 Achteck / Achtkant Achteck / Achtkant |
$$I_y=I_z=1.8595·B^4$$$$I_y=I_z=\frac{1+2·\sqrt{2}}{6}·R^4=0.6381·R^4$$ | $$W_y=W_z=1.5404·B^3$$$$W_y=W_z=0.6906·R^3$$ |
| R ist der Umkreisradius | ||
Wie man auf die hier angeführten Formeln kommt, wird auf dieser Unterseite gezeigt:
Zusammenhang Widerstandsmomente < > Flächenträgheitsmomente
Mit Hilfe der folgenden Formeln können bei bekanntem Flächenträgheitsmoment und bekannten Randfaserabständen die Widerstandsmomente berechnet werden. Das Widerstandsmoment bekommt man, indem man das jeweilige Flächenträgheitsmoment durch den Randfaserabstand dividiert. Ist das Profil bezüglich einer Achse symmetrisch, bekommt man für diese Achse nur ein Widerstandsmoment.
Die Formel zur Berechnung des Widerstandsmoments Wy bezüglich der y-Achse lautet:
$$W_{y_{1,2}}=\frac{I_y}{e_{1,2}}$$
Die Formel für das Widerstandsmoment Wz bezüglich der z-Achse lautet:
$$W_{z_{1,2}}=\frac{I_z}{e_{3,4}}$$
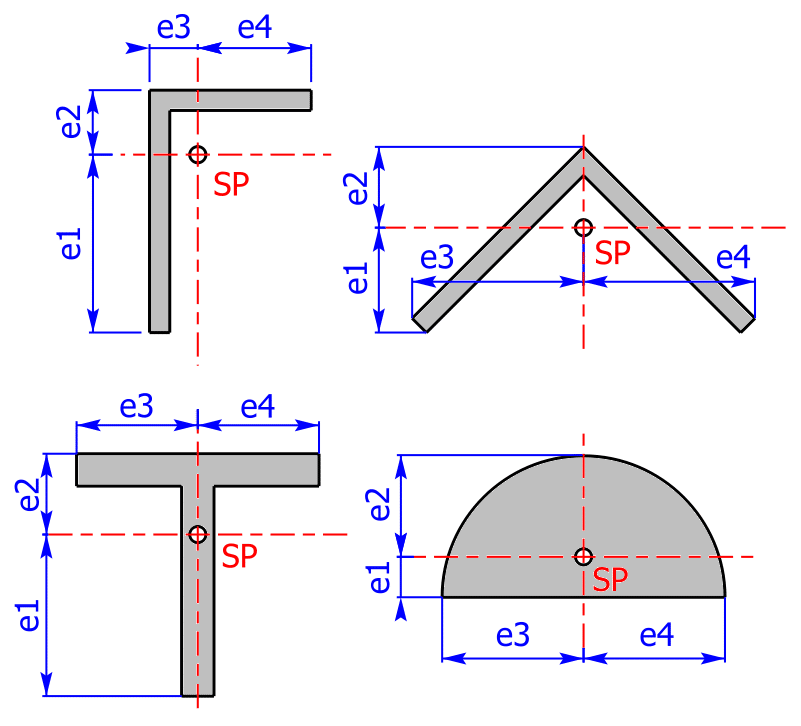
| Iy | Flächenträgheitsmoment bezüglich der y-Achse |
| Iz | Flächenträgheitsmoment bezüglich der z-Achse |
| e1 | unterer Randfaserabstand in z-Richtung |
| e2 | oberer Randfaserabstand in z-Richtung |
| e3 | linker Randfaserabstand in y-Richtung |
| e4 | rechter Randfaserabstand in y-Richtung |
SP ist die Abkürzung für den Flächenschwerpunkt, der sich in der Mitte des Koordinatensystems – also im sogenannten Koordinatenursprung – befindet.
Formel für polares Flächenträgheitsmoment
Das polare Flächenträgheitsmoment Ip ist die Summe der beiden axialen Flächenträgheitsmomente Iy und Iz und wird daher mit folgender Formel berechnet:
$$I_p=I_y+I_z$$
Nur bei kreisförmigen Querschnitten sind polares Flächenträgheitsmoment Ip und Torsionsträgheitsmoment It gleich groß, siehe auch Formeln im nächsten Kapitel:
$$I_p=I_t$$
Formeln für Torsionsträgheitsmomente & Torsionswiderstandsmomente
Anmerkungen:
- Es ist zu beachten, dass die in der Tabelle angeführten Formeln für nicht kreisförmige Flächen Näherungen sind und daher nur bei relativ dünnen Wandstärken gelten!
- Für tmin ist entweder b oder h einzusetzen, je nachdem, welche dieser Größen kleiner ist.
- Ähnliches gilt für tmax: Auch dafür ist b oder h einzusetzen, diesmal aber der größere der beiden Werte.
| Querschnittsprofil | Torsionsträgheitsmomente | Torsionswiderstandsmomente |
 Rundstange (Kreis) |
$$I_t=I_p=\frac{\pi·D^4}{32}$$ | $$W_t=W_p=\frac{\pi·D^3}{16}$$ |
 Rundrohr (Kreisring) |
$$I_t=I_p=\frac{\pi·(D^4-d^4)}{32}$$ | $$W_t=W_p=\frac{\pi·(D^4-d^4)}{16·D}$$ |
 Quadrat |
$$I_t=0.141·B^4$$ | $$W_t=0.208·B^3$$ |
 Rechteck- Hohlprofil |
$$I_t=\frac{2·(b_3·h_3)^2}{\frac{b_3}{h}+\frac{h_3}{b}}$$ | $$W_t=2·b_3·h_3·t_{min}$$ |
| $$b_3=B-b\qquad h_3=H-h$$ | ||
 I- bzw. H-Profil |
$$I_t=\frac{1.3}{3}·(2·B·h^3+h_4·b^3)$$ | $$W_t=\frac{I_t}{t_{max}}$$ |
| $$h_4=H – 2·h$$ | ||
 C- bzw. U-Profil |
$$I_t=\frac{1.12}{3}·(2·B·h^3+h_4·b^3)$$ | $$W_t=\frac{I_t}{t_{max}}$$ |
| $$h_4=H – 2·h$$ | ||
 T-Profil |
$$I_t=\frac{1.12}{3}·(B·h^3+h_3·b^3)$$ | $$W_t=\frac{I_t}{t_{max}}$$ |
| $$h_3=H – h$$ | ||
 L-Profil |
$$I_t=\frac{0.99}{3}·(B·h^3+h_3·b^3)$$ | $$W_t=\frac{I_t}{t_{max}}$$ |
| $$h_3=H – h$$ | ||
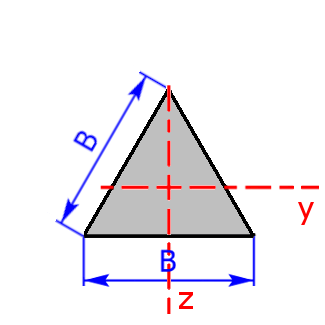 Gleichseitiges Dreieck |
$$I_t=\frac{B^4}{46.19}\qquad H=\frac{\sqrt{3}}{2}·B$$ | $$W_t=\frac{B^3}{20}$$ |
 Sechseck/Sechskant |
$$I_t=1.04·B^4$$ | $$W_t=0.977·B^3$$ |
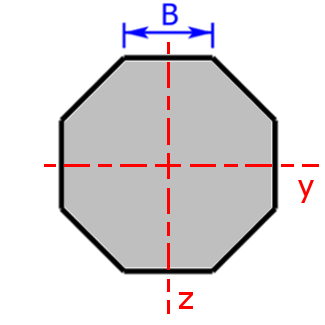 Achteck/Achtkant |
$$I_t=3.67·B^4$$ | $$W_t=2.60·B^3$$ |
Werbung
Seite erstellt am 09.06.2019. Zuletzt geändert am 27.07.2022.