Hier findest du die Formeln zur Berechnung der Druck- bzw. Zugspannungen. Man nennt sie Normalspannungen, da diese Spannungen normal zur Schnittfläche stehen. Zudem werden die Formeln zur Bestimmung der Längenänderung eines Stabes unter Belastung und zur Ermittlung der Dehnung in Kraftrichtung angegeben (Hook’sches Gesetz).
Am Ende wird anhand zweier Beispiele beschrieben, wie man bei der Berechnung eines Verbundstabes vorgeht. Ein Verbundstab besteht aus mehreren, unterschiedlichen Werkstoffen.
Link zu Unterseite:
Werbung
Formel zur Berechnung der Normalspannung
Die Normalspannung berechnet man, indem man die Zugkraft bzw. die Druckkraft durch die ursprüngliche Querschnittsfläche des Stabes dividiert. Die Formel zur Berechnung der Normalspannung, die auch als Zug- oder Druckspannung bezeichnet wird, lautet also:
$$\sigma_{z,\ d}=\frac{F}{A}$$
| σz, d | Druck- bzw. Zugspannung in N/mm² |
| F | Zug- bzw. Druckkraft in N; bei Druck-beanspruchung negatives Vorzeichen |
| A | Unbelastete Querschnittsfläche in mm² |
Hook’sches Gesetz und Dehnung
Den Zusammenhang zwischen Spannung und Dehnung in Richtung der Belastung stellt das sogenannte Hooksche Gesetz dar. Die Normalspannung ist das Produkt aus Elastizitätsmodul und Dehnung:
$$\sigma=E·\epsilon$$
| σ | Normalspannung in N/mm² |
| E | E-Modul in N/mm² |
| Ɛ | Dehnung in Kraftrichtung; dimensionslos |
Die Dehnung in Kraftrichtung ist dabei wie folgt definiert, wobei für die Normalspannung σ die rechte bzw. die untere Formel zu verwenden ist:
Dehnung in %
$$\epsilon=\frac{\Delta l}{l_0}·100$$
Dehnung
$$\epsilon=\frac{\Delta l}{l_0}$$
| Ɛ | Dehnung in Kraftrichtung; in % oder dimensionslos |
| Δl |
Längenänderung in mm; positiv bei Zug-, negativ bei Druckbelastung |
| l0 | ursprüngliche bzw. ungedehnte Länge des Stabes in mm |
Ist die Dehnung negativ, spricht man von einer Stauchung. Dies trifft bei einer Druckbeanspruchung zu.
Gesamtlänge
Die Gesamtlänge des Stabes unter Last bekommt man, indem man die unbelastete Stablänge l0 zur Längenänderung Δl addiert:
$$l_{Last}=l_0+\Delta l$$
Beispiele
Verbundstab
Ein Stab mit der Länge l0 besteht aus zwei verschiedenen Werkstoffen, deren E-Modul sich unterscheidet – innen aus dem Material 1 mit dem E-Modul E1 und außen aus dem Material 2 mit dem E-Modul E2. Die Querschnittflächen A1 und A2 sind bekannt. Gesucht sind die Zugspannungen und die Verlängerung dieses Stabes, die sich aufgrund der Belastung F ergeben, siehe Abbildung.
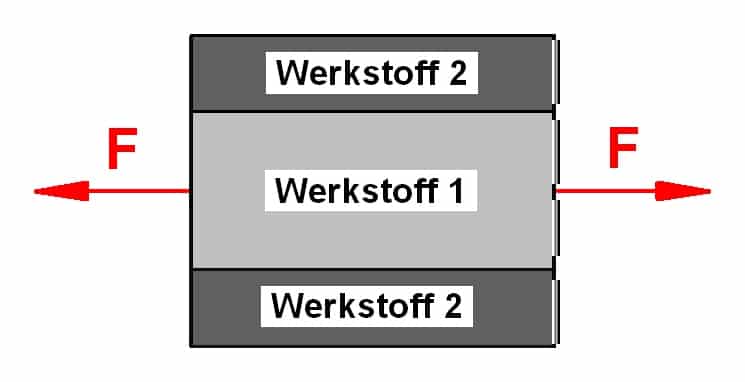
Lösung
Die Längenänderung in den beiden Schichten muss offensichtlich gleich groß sein:
$$\Delta l=\Delta l_1=\Delta l_2$$
Die Dehnung ist ε = Δl/l0. Somit müssen laut der Formel auch die Dehnungen ident sein:
$$\epsilon=\epsilon_1=\epsilon_2$$
$$\sigma_1=E_1·\epsilon_1=E_1·\epsilon$$
$$\sigma_2=E_2·\epsilon_2=E_2·\epsilon$$
Umformen auf ε und gleichsetzen von ε ergibt:
Nun formt man auf die Zugspannung σ1 um:
$$\sigma_1=\frac{E_1}{E_2}·\sigma_2$$
Da E1 und E2 laut Angabe nicht ident sind, müssen die Spannungen σ1 bzw. σ2 und damit auch die Kräfte in den beiden Werkstoffen unterschiedlich sein, da sonst die obige Gleichung nicht stimmen kann. Das Problem ist nun, dass wir eine Gleichung mit zwei Unbekannten haben, die beiden Zugspannungen σ1 und σ2. Wir müssen also eine weitere Gleichung aufstellen. Es gilt für die Kräfte:
Die Summe der beiden Teilkräfte F1 und F2 muss die Gesamtkraft F ergeben:
In diese Gleichung kann man nun die zuvor ausgedrückte Spannung σ1 einsetzen und zunächst die gesuchte Spannung σ2 herausheben:
Dividieren durch den Klammerausdruck ergibt schließlich die Zugspannung σ2:
$$\sigma_2=\frac{F}{\frac{E_1}{E_2}·A_1+A_2}$$
Somit kann auch die Zugspannung σ1 berechnet werden, indem man in die schon zuvor aufgestellte Gleichung einsetzt:
Die Verlängerung des Stabes bekommt man mit einer der folgenden Formeln, die zu Beginn hergeleitet wurden:
Stab aus zwei Werkstoffen
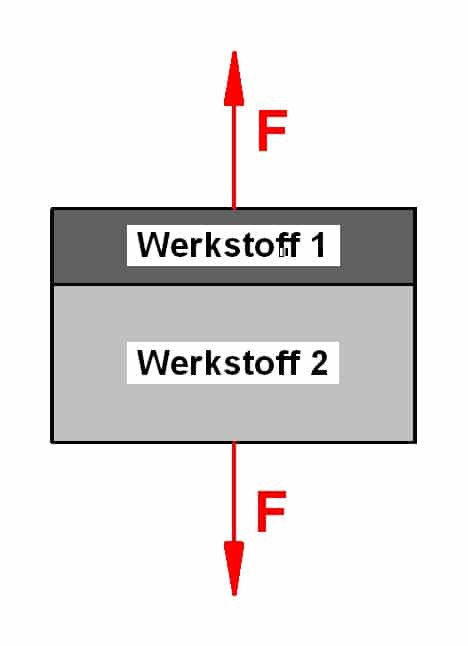
Die nächste bzw. nebenstehende Abbildung zeigt wie schon zuvor einen Stab aus zwei verschiedenen Werkstoffen, deren E-Modul sich unterscheidet. Allerdings sind nun die beiden Materialien hintereinander angeordnet. Die Querschnittflächen A1 und A2 sind bekannt.
Gesucht sind wieder die Zugspannungen und die Verlängerung dieses Stabes, die sich aufgrund der Belastung F ergeben.
Lösung
In diesem Fall sind die Kräfte in beiden Teilen gleich groß:
$$F_1=F_2=F$$
Für die zwei Zugspannungen gilt daher:
$$\sigma_1=\frac{F}{A_1}\qquad \sigma_2=\frac{F}{A_2}$$
Sind auch die beiden Querschnittsflächen gleich groß, folgt:
$$\sigma_1=\sigma_2=\sigma=\frac{F}{A_1}=\frac{F}{A_2}$$
Die gesamte Verlängerung des Stabes setzt sich aus den beiden Teilverlängerungen zusammen:
$$\Delta l=\Delta l_1+\Delta l_2$$
Mit
erhält man schließlich die Formel für die gesamte Verlängerung des Stabes:
$$\Delta l=\frac{\sigma_1·l_0}{E_1}+\frac{\sigma_2·l_0}{E_2}$$
Werbung
Seite erstellt am 22.01.2022. Zuletzt geändert am 17.04.2023.