Auf dieser Seite findest du ausführliche Informationen – also auch Formeln und Beispiele mit grafischen Darstellungen – zu den Sinusschwingungen:
- Wie sieht eine Sinusschwingung aus – inklusive grafische Darstellung.
- Welche Parameter kann man verändern und wie wirkt sich das auf die Darstellung der harmonischen Sinusschwingung aus.
- Ermitteln dieser Parameter mittels Formeln und damit der Funktionsgleichung aus einer Grafik.
- Auch der Zusammenhang zwischen der Sinus- und der der Cosinusfunktion wird erläutert.
Inhaltsverzeichnis
Grundlagen zur Sinusfunktion
Bei der Sinusfunktion handelt es sich um eine der wichtigsten mathematischen Funktionen. Die Funktionsgleichung vom Sinus lautet:
$$f(x)=sin(x)\quad oder:\quad y=sin(x)$$
So sieht die grafische Darstellung der Sinusfunktion aus:
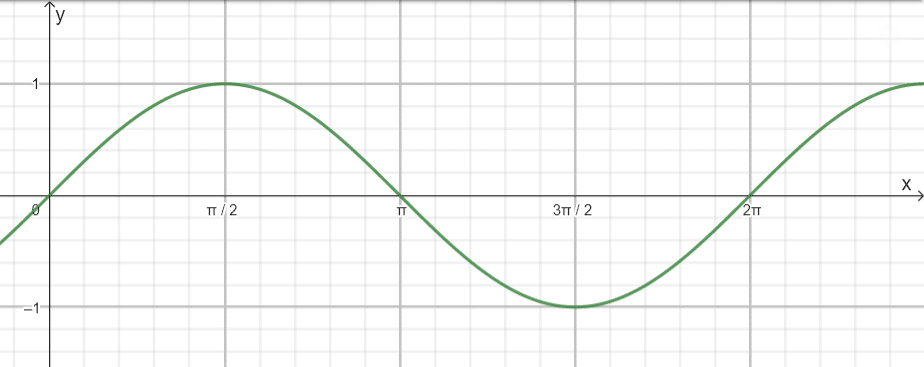
In der Regel wird der Winkel – in dieser Grafik und in der Formel mit x bezeichnet – in Radiant angegeben, der Taschenrechner ist dann im Modus RAD zu verwenden.
Wie man erkennen kann, liegen alle y-Werte – also die Funktionswerte f(x) – stets zwischen -1 und +1. Die Periodendauer T beträgt 2 π oder 360° – das heißt, alle 2·π wiederholt sich die Funktion.
Allgemeine harmonische Sinus-Schwingung
Die Funktionsgleichung einer allgemeinen harmonischen Schwingung wird wie folgt angegeben:
$$f(x)=A·sin(\omega ·x+φ)+d$$
Bei der Sinusfunktion sind alle diese Parameter gleich 1, wobei man die 1 in der Regel nicht anschreibt. Eine ausführliche Erklärung aller in dieser Formel vorkommenden Variablen gibt es nach der folgenden Darstellung einer harmonischen Sinus-Schwingung:
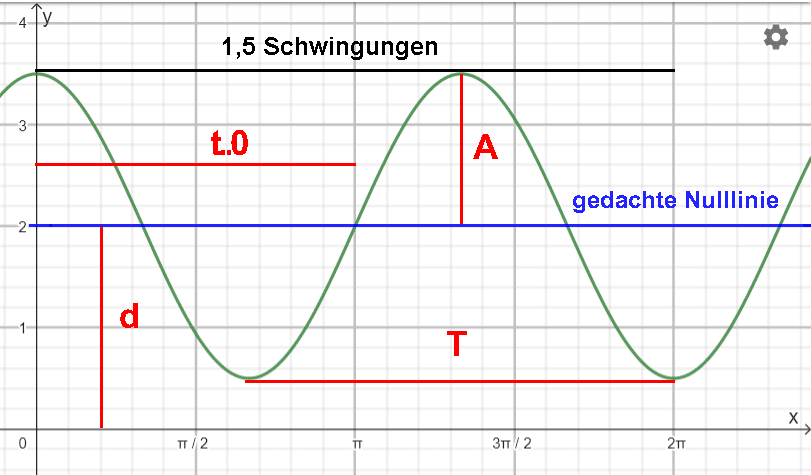
Die Funktionsgleichung dieser Sinusschwingung lautet:
$$f(x)=1,5·sin\left(1,5·x+\frac{\pi}{2}\right)+2$$
Etwas weiter unten auf dieser Seite wird im Zuge eines Beispiels beschrieben, wie man auf diese Gleichung kommt.
Erklärung der Variablen
- A ist die sogenannte Amplitude. Darunter versteht man die maximale Auslenkung vom arithmetischen Mittelwert, also von der gedachten Nulllinie. Werte größer als 1 bewirken eine Streckung in y-Richtung, Werte kleiner als 1 eine Stauchung. Ist die Amplitude negativ, erfolgt eine Spiegelung um die x-Achse.
- Als ω wird die Kreisfrequenz bezeichnet. Werte größer als 1 ergeben eine Stauchung in x-Richtung und die Frequenz f wird erhöht. Werte kleiner als 1 bewirken eine Streckung in x-Richtung, wodurch die Frequenz verringert wird. Die Kreisfrequenz kann in einfachen Fällen direkt aus einer Grafik bestimmt werden oder mittels Formel berechnet werden.
- φ ist der Phasenwinkel. Damit kann die Funktion in x-Richtung verschoben werden. Positive Werte ergeben eine Verschiebung nach links – also in die negative x-Richtung -, negative Werte eine Verschiebung nach rechts. Der Phasenwinkel kann nur dann direkt aus einer Grafik abgelesen werden, wenn ω gleich 1 ist. Andernfalls benötigt man eine Formel, die im Anschluss zu finden ist.
- Mit dem Parameter d erfolgt eine Verschiebung in y-Richtung: Positive Werte bewirken eine Verschiebung nach oben, negative Werte nach unten. Es handelt sich dabei um den Abstand zwischen der x-Achse und der gedachten Nulllinie.
Kreisfrequenz ω
Die Kreisfrequenz ω wird mit der folgenden Formel berechnet:
$$\omega=\frac{2·\pi}{T}$$
T wird als Periodendauer bezeichnet. Es handelt sich dabei um jene Zeit, die eine vollständige Schwingung in Anspruch nimmt, also um den kleinsten Abstand zwischen zwei “Bergen” (=Hochpunkte) bzw. “Tälern” (=Tiefpunkte).
Mit der Defintion der Frequenz f
$$f=\frac{1}{T}$$
kann man die Kreisfrequenz ω auch wie folgt anschreiben:
$$\omega=2·\pi·f$$
Phasenwinkel bzw. Phasenverschiebung φ
Die Phasenverschiebung φ bestimmt man wie folgt, wobei unbedingt das negative Vorzeichen zu beachten ist:
$$φ=-t_0·\omega$$
Der Wert t0 ist der Abstand von der y-Achse des Koordinatensystems zum ersten Anstieg der Funktion.
Beispiel: Finden der Funktionsgleichung
Aus der folgenden, schon bekannten Grafik soll nun die Funktionsgleichung ermittelt werden:

Am besten fängt man der Einfachheit halber mit der Amplitude A an: Der höchste Punkt der Funktion hat den y-Wert 3,5 und die gedachte Nulllinie schneidet bei y=2 die y-Achse. Die Differenz dieser beiden Werte ergibt die Amplitude:
$$A=3,5-2\Rightarrow A=1,5$$
Genauso einfach bekommt man den Parameter d. Ganz offensichtlich befindet sich die gedachte Nulllinie 2 Einheiten über der x-Achse, sie wurde also um 2 nach oben verschoben:
$$d=2$$
Mit etwas Übung sieht man, dass sich in der “normalen” Periodendauer von 2·π hier 1,5 Schwingungen statt nur 1 Schwingung ausgehen. Daher gilt für die Kreisfrequenz ω:
$$\omega=1,5$$
Alternativ ist die Ermittlung der Kreisfrequenz mit der Formel möglich, allerdings ist die Periodendauer T in diesem Beispiel nicht einfach abzulesen – sie beträgt etwa
$$0,7·\frac{\pi}{2}+\pi=4,2412$$
Einsetzen in die Formel für die Kreisfrequenz ergibt:
$$\omega=\frac{2·\pi}{T}=\frac{2·\pi}{4,2412} \Rightarrow \omega=1,48$$
was gerundet 1,5 ergibt.
Zuletzt erfolgt die Bestimmung der Phasenverschiebung. Der Abstand t0 beträgt genau π, daher ergibt sich für die Phasenverschiebung φ mit der Formel:
$$φ=-t_0·\omega\Rightarrow φ=-\pi·1,5\Rightarrow φ=-\frac{3}{2}·\pi$$
Möchte man einen positiven Phasenverschiebungswinkel, gibt man einfach 2·π dazu:
$$φ=-\frac{3}{2}·\pi+2·\pi\Rightarrow φ=\frac{\pi}{2}$$
Damit kann man nun alle berechneten Parameter in die Funktionsgleichung einsetzen. Man bekommt:
$$f(x)=1,5·sin\left(1,5·x+\frac{\pi}{2}\right)+2$$
Zusammenhang zwischen Sinus- und Cosinusfunktion
Den Cosinus bzw. Kosinus bekommt man aus der Sinusfunktion mittels Phasenverschiebung um π/2:
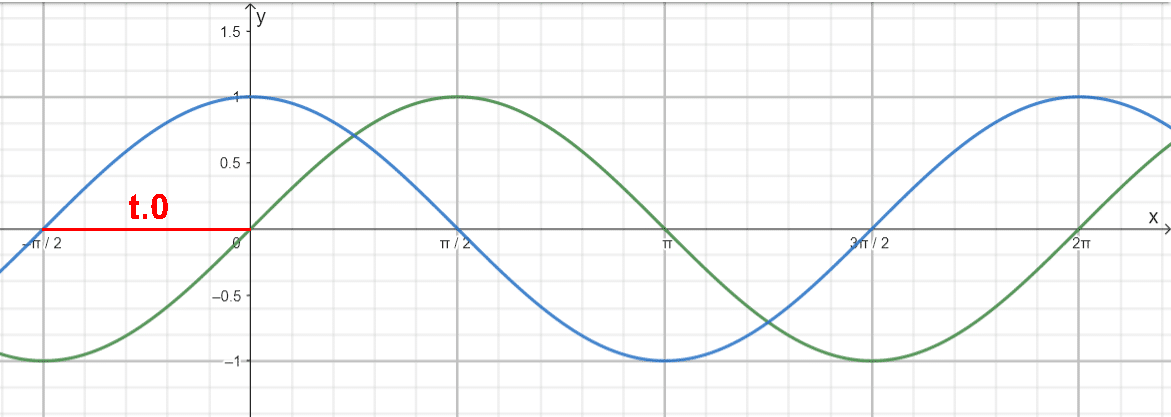
Da die Kreisfrequenz ω gleich 1 ist – beim Cosinus handelt es sich ja nur um eine verschobene Sinusfunktion-, kann der Phasenwinkel direkt aus der Grafik abgelesen werden. Es gilt mit t0 = -π/2
$$φ = -t_0 =-\left(-\frac{\pi}{2}\right) \Rightarrow φ =\frac{\pi}{2}$$
wobei die zwei negativen Vorzeichen zu beachten sind oder man berechnet φ mit der Formel
$$φ=-t_0·\omega\Rightarrow φ=-\left(-\frac{\pi}{2}·1\right)=\frac{\pi}{2}$$
Es gilt daher:
$$cos(x)=sin\left(x+\frac{\pi}{2}\right)$$
Seite erstellt am 29.01.2023. Zuletzt geändert am 06.02.2023.