Auf dieser Seite findest du alles zum Thema Integrieren, also die Stammfunktionen von wichtigen Funktionen, die Integrationsregeln samt ein paar Beispielen und weitere Formeln, zum Beispiel zum Berechnen des Volumens von Drehkörpern. Beim Integrieren geht es darum, für eine gegebene Funktion f(x) die Stammfunktion F(x) – also das Integral – zu bestimmen, was aber nicht immer so einfach möglich ist.
Integrieren ist das Gegenteil von differenzieren. Vor allem in der Schule ist auch der Begriff aufleiten als Gegenstück zu ableiten recht geläufig. Willst du nur Integrale berechnen, ist die Seite integralrechner.de sehr zu empfehlen.
Inhaltsverzeichnis
Werbung
Wichtige Stammfunktionen
Von manchen Funktionen lässt sich die Stammfunktion ziemlich einfach bilden. Das trifft zum Beispiel auf Potenzfunktionen zu. Für andere Funktionen findet man deren Integrale in Tabellen bzw. ist die Berechnung teilweise nur recht schwierig und mit viel Erfahrung möglich.
Wichtig:
Niemals auf die Integrationskonstante C vergessen!
Stammfunktion einer konstanten Funktion
Das Integral der konstanten Funktion f(x) = k wird wie folgt berechnet:
$$y=f(x)=k⟹F(x)=∫k\, dx=k·x+C$$
| k | Konstante |
| F(x) | Stammfunktion der Funktion f(x) |
| dx | gibt an, dass nach x zu integrieren ist |
| C | Integrationskonstante; ihr Wert ist prinzipiell unbekannt, kann aber bei gegebenen Anfangsbedingungen berechnet werden. |
Das dx am Ende des Integrals besagt, dass die Funktion f nach x zu integrieren ist. Eine konstante Funktion wird also integriert, indem man die Konstante k mit x multipliziert und am Ende eine Integrationskonstante C ergänzt.
Die Integration der Zahl 0 ergibt die Integrationskonstante C:
$$∫0\, dx=C$$
Beispiel
Die folgende Funktion f(x) ist zu integrieren:
$$y=f(x)=5⟹F(x)=∫5\, dx=5·x+C$$
Stammfunktion einer Potenzfunktion
Das Integral einer Potenzfunktion wird auf folgende Weise berechnet:
$$y=f(x)=x^n⟹F(x)=∫x^n\, dx=\frac{x^{n+1}}{n+1}+C$$
n Exponent oder Hochzahl; konstant
Die Stammfunktion einer Potenzfunktion bekommt man folglich durch Erhöhung der Hochzahl um 1 und anschließender Division durch diese um 1 vermehrte Hochzahl. Die Integrationskonstante C muss auch in diesem Fall hinzugefügt werden.
Beispiel
Es ist das Integral von x² zu bestimmen:
$$∫x^2\, dx=\frac{x^{2+1}}{2+1}+C⟹F(x)=\frac{x^3}{3}+C$$
Formelsammlung: Stammfunktionen von wichtigen Funktionen
Für einige grundlegende Funktionen sind hier ihre Integrale angeführt. Auch die Stammfunktionen einer konstanten Funktion und einer Potenzfunktion werden der Vollständigkeit halber nochmals angeführt.
Die Integrationskonstante C wurde in dieser Formelsammlung aus Platzgründen weggelassen, sie muss bei Berechnungen aber immer angegeben werden!
0
$$\int 0 \, dx=C$$
Konstante Funktion
$$\int k \, dx=k·x$$
Potenzfunktion (n≠-1)
$$∫x^n\, dx=\frac{x^{n+1}}{n+1}$$
Potenzfunktion (n=-1)
$$∫x^{-1}\, dx=∫\frac{1}{x}\, dx=ln|x|$$
Weitere Funktionen
$$∫\frac{1}{x+a}\, dx=ln|x+a|$$
$$∫\frac{1}{(x+a)^2}\, dx=-\frac{1}{x+a}$$
Natürliche Exponentialfunktion
$$\int e^x\, dx=e^x$$
$$\int e^{a·x}\, dx=\frac{e^{a·x}}{a}$$
Exponentialfunktion
$$\int a^x\, dx=\frac{a^x}{ln(a)}$$
Natürliche Logarithmusfunktion
$$\int ln(x)\, dx=x·ln(x)-x$$
Logarithmusfunktion
$$\int \log_a (x)\, dx=$$
$$\frac{1}{ln(a)}·(x·ln(x)-x)$$
Sinusfunktion
$$\int sin(x)\, dx=-cos(x)$$
Kosinusfunktion
$$\int cos(x)\, dx=sin(x)$$
Tangensfunktion
$$\int tan(x)\, dx=-ln|cos(x)|$$
Kotangensfunktion
$$\int cot(x)\, dx=ln|sin(x)|$$
Weitere Funktionen
$$\int \frac {1}{cos^2(x)}\, dx=tan(x)$$
$$\int \frac {1}{sin^2(x)}\, dx=-cot(x)$$
$$\int \frac {1}{\sqrt{1-x^2}}\, dx=arcsin(x)$$
$$\int \frac {-1}{\sqrt{1-x^2}}\, dx=arccos(x)$$
$$\int \frac {1}{1+x^2}\, dx=arctan(x)$$
$$\int \frac {-1}{1+x^2}\, dx=arccot(x)$$
$$\int \frac {1}{\sqrt{x^2+1}}\, dx=arcsinh(x)$$
$$\int \frac {1}{\sqrt{x^2-1}}\, dx=arccosh(x)$$
für |x| < 1 gilt:
$$\int \frac {1}{1-x^2}\, dx=arctanh(x)$$
für |x| > 1 gilt:
$$\int \frac {1}{1-x^2}\, dx=arccoth(x)$$
$$\int sin(a·x)·cos(a·x)\, dx=$$
$$\frac{1}{2·a}·sin^2(a·x)$$
$$\int \frac{\, dx}{sin(a·x)·cos(a·x)}=$$
$$\frac{1}{a}·ln|tan(a·x)|$$
Zusammenhang
$$\int \frac{f'(x)}{f(x)}\, dx=ln|f(x)|$$
Rechenregeln für das Integrieren
Terme, die durch Plus- oder Minuszeichen getrennt sind, werden einzeln integriert:
$$∫\left[f(x)±g(x)\right]\, dx=∫f(x)\, dx±∫g(x)\, dx$$
Alle Konstanten, die nicht durch Plus- oder Minuszeichen von einander getrennt sind, kann man vor das Integral schreiben:
$$∫[k·f(x)]\, dx=k·∫f(x)\, dx$$
k Konstante
Beispiel
Das Integral der Funktion f(x) ist zu bestimmen:
$$y=f(x)=e^{2·x}+3·x^2-6⟹F(x)=∫\left[e^{2·x}+3·x^2-6\right]\, dx$$
Anwenden der obigen Rechenregeln ergibt:
$$F(x)=∫e^{2·x}\, dx+3·∫x^2\, dx-∫6\, dx$$
Die einzelnen Integrale berechnet man nun mit Hilfe der Formelsammlung Stammfunktionen von wichtigen Funktionen:
$$F(x)=\frac{e^{2·x}}{2}+\frac{3·x^3}{3}-6·x+C=\frac{e^{2·x}}{2}+x^3-6·x+C$$
Partielle Integration
Das Integral eines Produkts von zwei Funktionen f(x) und g(x) kann manchmal mittels (mehrfacher) partieller Integration berechnet werden. Zu beachten ist eine sinnvolle Reihenfolge der Funktionen, also ob man das Integral als f(x) · g(x) oder g(x) · f(x) anschreibt. Die Funktion g(x) sollte sich beim Ableiten vereinfachen, siehe Beispiel.
$$\int[f(x)·g(x)]\, dx=F(x)·g(x)-\int [F(x)·g'(x)] \, dx$$
| F(x) | Stammfunktion der Funktion f(x) |
| g'(x) | 1. Ableitung von g(x) |
Beispiel
Integriere:
$$∫\left[3·x^2·sin(x)\right]\, dx$$
Die Konstante, also die Zahl 3, kann man vor das Integral setzen. In diesem Beispiel ist es notwendig, den Term x² als Funktion g(x) zu wählen, da sich dieser Term beim Ableiten vereinfacht, während sin(x) beim Differenzieren zu cos(x) würde, was nichts bringen würde. Man erhält:
$$F(x)=3·∫\left[sin(x)·x^2\right]\, dx$$
Dann berechnet man sich die einzelnen Terme zur Anwendung der obigen Formel. Das Integral von sin(x) findet man in der Formelsammlung Stammfunktionen von wichtigen Funktionen:
$$f(x)=sin(x)⟹F(x)=-cos(x)$$
$$g(x)=x^2⟹g'(x)=2·x$$
Einsetzen in die Formel für die partielle Integration ergibt:
$$3·\int\left[sin(x)·x^2\right]\, dx=3·\{-cos(x)·x^2-\int [-cos(x)·2·x] \, dx\}$$
Das sich nun ergebende Integral kann noch immer nicht gelöst werden, daher muss man nochmals partiell integrieren. Die Konstante setzt man am besten wieder vor das Integralzeichen, minus mal minus ergibt plus. Man bekommt:
$$3·\{-cos(x)·x^2+2·\int [cos(x)·x] \, dx\}$$
$$f(x)=cos(x)⟹F(x)=sin(x)$$
$$g(x)=x⟹g'(x)=1$$
Nochmaliges Einsetzen in die Formel für die partielle Integration ergibt:
$$3·\{-cos(x)·x^2+2·\{sin(x)·x-\int [sin(x)·1] \, dx\}\}$$
Das noch verbleibende Integral kann nun problemlos berechnet werden:
$$3·\{-cos(x)·x^2+2·\{sin(x)·x-[-cos(x)]\}\}$$
Durch Vereinfachen, Ausmultiplizieren der Klammern und Herausheben bekommt man das Ergebnis, wobei man zuletzt auch die Integrationskonstante anschreibt:
$$6·x·sin(x)+cos(x)·\left [6-3·x^2\right ]+C$$
Integration durch Substitution
Viele Integrale lassen sich oft nur mithilfe der Substitution ermitteln. Schwierig ist oftmals das Finden einer passenden Substitution. Mit der folgenden Formel werden nur wenige etwas anfangen – die nächsten Beispiele sind wesentlich verständlicher:
$$\int f(x)\, dx=\int[f(g(u))·g'(u)]\, du$$
Beispiel 1
Die folgende Funktion f(x) soll integriert werden:
$$y=f(x)=(3+x)^2⟹F(x)=∫(3+x)^2\, dx$$
Es gibt nun 2 Möglichkeiten, das Integral der Funktion f(x) zu bestimmen:
1) Anwenden der 1. binomischen Formel
$$f(x)=(3+x)^2⟹f(x)=9+6·x+x^2$$
Dieser Ausdruck kann nun ganz einfach integriert werden:
$$F(x)=\int (9+6·x+x^2)\, dx⟹F(x)=9·x+3·x^2+\frac{x^3}{3}+C$$
2) Substituieren
Zunächst setzt man den Ausdruck in der Klammer gleich u:
$$u=3+x$$
Dann leitet man u nach x ab und formt auf dx um:
$$\frac{du}{dx}=1⟹dx=du$$
Einsetzen für 3 + x = u und dx = du und anschließendes Integrieren ergibt:
$$F(x)=∫(3+x)^2\, dx⟹F(u)=∫(u)^2\, du=\frac{u^3}{3}+C$$
Einsetzen von u = 3 + x liefert das Ergebnis:
$$F(x)=\frac{(3+x)^3}{3}+C$$
Unterschiedliche Ergebnisse für beide Varianten – Erklärung
Es ist nicht offensichtlich, dass die Ergebnisse aus 1) und 2) äquivalent sind. Daher wendet man auf das letzte Ergebnis noch eine binomische Formel an:
$$F(x)=\frac{3^3+3·3^2·x+3·3·x^2+x^3}{3}+C$$
Vereinfachen ergibt:
$$F(x)=9+9·x+3·x^2+\frac{x^3}{3}+C$$
Die beiden Ergebnisse sind also fast gleich, sie unterscheiden sich nur durch die Konstante 9. Das ist aber für Stammfunktionen zulässig.
Beispiel 2
Es ist die Stammfunktion F(x) der Funktion f(x) zu berechnen:
$$f(x)=\frac{1}{2·x}$$
Auch hier gibt es 2 Möglichkeiten, dieses Integral zu ermitteln:
1) Vorziehen der Konstanten vor das Integral
$$F(x)=\int\frac{1}{2·x}\, dx⟹F(x)=\frac{1}{2}·\int\frac{1}{x}\, dx$$
Man bekommt:
$$F(x)=\frac{1}{2}·ln|x|+C$$
2) Substituieren
Als Erstes setzt man den Nenner gleich u:
$$u=2·x$$
Dann leitet man u nach x ab und formt auf dx um:
$$\frac{du}{dx}=2⟹dx=\frac{du}{2}$$
Einsetzen für 2·x = u und dx = du/2 und anschließendes Integrieren ergibt:
$$F(u)=\int\frac{1}{u}·\, \frac{du}{2}⟹F(u)=\frac{1}{2}·ln|u|+C$$
Einsetzen von u = 2·x liefert das Ergebnis:
$$F(x)=\frac{1}{2}·ln|2·x|+C$$
Unterschiedliche Ergebnisse für beide Varianten – Erklärung
Es sieht so aus, als wären die Ergebnisse aus 1) und 2) nicht äquivalent. Wenn man jedoch beide Ergebnisse ableitet, bekommt man jeweils die Angabe. Für Fall 1:
$$F'(x)=f(x)=\left(\frac{1}{2}·ln|x|+C\right)’=\frac{1}{2}·\frac{1}{x}⟹\frac{1}{2·x}$$
Für Fall 2 (innere Ableitung nicht vergessen!):
$$F'(x)=f(x)=\left(\frac{1}{2}·ln|2·x|+C\right)’=\frac{1}{2}·\frac{1}{2·x}·2⟹\frac{1}{2·x}$$
Also sind die beiden gefundenen Lösungen tatsächlich Stammfunktionen von f(x). Dies lässt sich auch mit Hilfe der Rechenregeln für den Logarithmus zeigen:
$$F(x)=\frac{1}{2}·ln|2·x|+C=\frac{1}{2}·\left[ln|2|+ln|x|\right]+C=\frac{1}{2}·ln|2|+\frac{1}{2}·ln|x|+C$$
Die beiden Ergebnisse sind also ähnlich, sie unterscheiden sich nur durch die Konstante 1/2·ln|2|. Das ist jedoch für Stammfunktionen zulässig.
Beispiel 3
Berechne das folgende Integral:
$$\int\frac{1}{(1+x)·\sqrt x}\, dx$$
Man substituiert die Wurzel aus x und drückt sich auch x aus:
$$u=\sqrt x=x^{\frac{1}{2}} ⇔ x=u^2$$
Die Ableitung von u nach x ist:
$$\frac{du}{dx}=\frac{1}{2}·x^{-\frac{1}{2}}=\frac{1}{2·\sqrt x}$$
Umformen nach dx ergibt:
$$dx=2·\sqrt x \, du$$
Einsetzen in die Angabe für x und dx und kürzen liefert:
$$F(x)=\int\frac{2·\sqrt x}{(1+u^2)·\sqrt x}\, du=2·\int\frac{1}{1+u^2}\, du$$
Dieses Integral ist in der Formelsammlung Stammfunktionen von wichtigen Funktionen zu finden. Man erhält:
$$F(x)=2·arctan(u)+C$$
Rückeinsetzen liefert schließlich das Ergebnis:
$$F(x)=2·arctan(\sqrt x)+C$$
Bestimmtes Integral & Flächeninhalte
Ein bestimmtes Integral erkennt man an den Integrationsgrenzen a und b. Sein Wert wird berechnet, indem man die Grenzen a und b in die Stammfunktion F(x) einsetzt und diese beiden Terme anschließend voneinander abzieht:
$$\int_a^b f(x)\, dx=F(b)-F(a)$$
a, b Integrationsgrenzen
Beispiel
Integriere:
$$\int_2^3(x^2-2·x)\, dx$$
Zunächst berechnet man das Integral, kürzt und schreibt die Grenzen dahinter an:
$$\left.\left[\frac{x^3}{3}-x^2+C\right]\right/_2^3$$
Dann setzt man die obere und die untere Grenze ein und zieht die beiden Terme von einander ab:
$$\left[\frac{3^3}{3}-3^2+C\right]-\left[\frac{2^3}{3}-2^2+C\right]=\left[9-9+C\right]-\left[\frac{8}{3}-4+C\right]=[C]-\left[-\frac{4}{3}+C\right]$$
Die Integrationskonstante C fällt weg und kann daher bei bestimmten Integralen immer weggelassen werden. Man erhält:
$$C+\frac{4}{3}-C=\frac{4}{3}$$
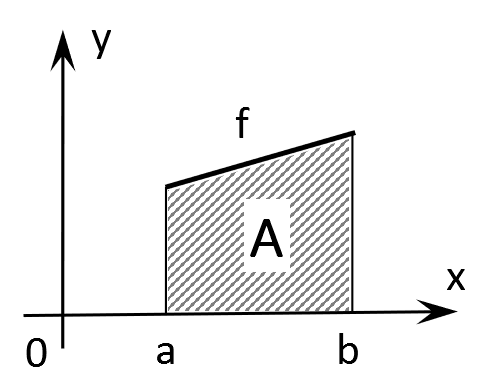
Flächeninhalt zwischen f(x) und der x-Achse
Schneidet die Funktion f(x) zwischen den Stellen a und b nicht die x-Achse (das heißt, dass sie in diesem Intervall keine Nullstellen hat), entspricht der Betrag des bestimmten Integrals der Fläche A zwischen der Funktion f(x) und der x-Achse im Intervall [a; b]. Die Buchstaben a und b entsprechen den Integrationsgrenzen:
$$A=\left|\int_a^b f(x)\, dx \right|$$
Flächeninhalt zwischen zwei Funktionen f(x) und g(x)
Den Flächeninhalt A zwischen zwei Funktionen f(x) und g(x) im Intervall [a; b] bestimmt man mit der folgenden Formel:
$$A=\int_a^b [f(x)-g(x)]\, dx$$
Dabei muss für alle x zwischen den Stellen a und b stets gelten: f(x) ≥ g(x). Das heißt, die Funktion f(x) muss sich immer über g(x) befinden.
Haben die beiden Funktionen mehrere gemeinsame Schnittpunkte, muss man das Integral in einzelne Bereiche aufteilen, damit die obere Bedingung auch immer erfüllt ist.
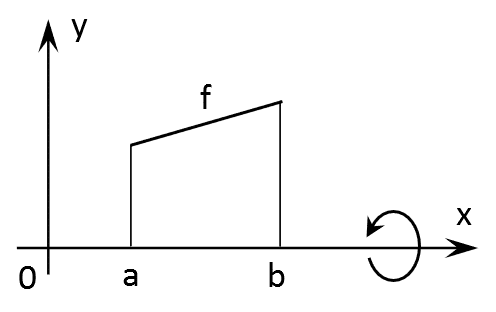
Volumen von Drehkörpern (Rotationskörpern)
Das Volumen V eines Rotationskörpers kann man mit Hilfe der Integralrechnung berechnen.
Die Formel für das Volumen V bei Drehung um die x-Achse lautet:
$$V=π·∫_a^b[f(x)]^2\, dx=π·∫_a^b y^2 \, dx$$
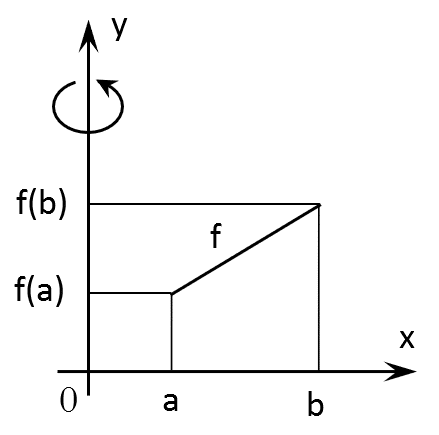
Bei Drehung um die y-Achse gilt für die Berechnung des Volumens V, wobei f -1 die Umkehrfunktion ist:
$$V=π·∫_{f(a)}^{f(b)}[f^{-1}(y)]^2\, dy=π·∫_{f(a)}^{f(b)} x^2 \, dy$$
Werbung
Seite erstellt am 23.06.2021. Zuletzt geändert am: