Auf dieser Seite findest du die Formeln zur Berechnung der maximal möglichen Geschwindigkeit in Kurven und zwar sowohl für Schienenfahrzeuge als auch für Straßenfahrzeuge. Für Schienenfahrzeuge ist normalerweise die freie Seitenbeschleunigung relevant, während für Straßenfahrzeuge in der Regel die Haftreibungszahl zwischen Reifen und Fahrbahn von Bedeutung ist.
Es werden sowohl die exakten Formeln als auch die vereinfachten Formeln angegeben. Zudem gibt es hier Skizzen und Tabellen mit typischen Werten für die minimalen Kurvenradien und die freie Seitenbeschleunigung.
Links zu Unterseiten:
Inhaltsverzeichnis
Werbung
Allgemeines
Der Faktor 3.6 am Ende der Formeln dient der Umrechnung von m/s in km/h. Die SI-Einheit ist m/s, allerdings können viele Menschen damit nicht so viel anfangen. Deshalb ist eine Angabe in km/h meist zweckmäßiger.
Erklärung der Variablen
In den folgenden Formeln kommen diese Variablen vor:
| v: | zulässige Geschwindigkeit in km/h |
| aq: | erlaubte freie Seitenbeschleunigung in m/s² |
| g: | Erdbeschleunigung in m/s² |
| µ: | Haftreibungszahl |
| r: | Radius in Gleismitte/Fahrbahnmitte in m |
| D: | vertikaler Abstand = Überhöhung |
| b: | horizontaler Abstand |
| α: | Steigungswinkel der Straße bzw. Bahnstrecke in ° |
| β: | Überhöhungswinkel in ° |
Anmerkungen:
- Die freie Seitenbeschleunigung aq, der Steigungswinkel α, der Überhöhungswinkel β und die Überhöhung D können auch negativ sein!
- Für kleine Winkel kann man in guter Näherung cos(α) und cos(β) gleich eins setzen. Das wird auch bei den vereinfachten Formeln so gemacht.
- Was man unter den Winkeln α und β genau versteht, wird im übernächsten Abschnitt anhand von Skizzen näher ausgeführt.
Vereinfachte Formeln
Für viele Anwendungen sind die folgenden, vereinfachten Formeln ausreichend. Für große Überhöhungen oder steile Straßen und auch für Achterbahnen sind die weiter unten befindlichen exakten Formeln zu gebrauchen.
Seitenbeschleunigung relevant (Schienenverkehr)
Wenn die freie Seitenbeschleunigung bekannt ist, erhält man die maximale Kurvengeschwindigkeit v mit einer Formel aus dem Gleisbau:
$$v=\sqrt{\left (a_q+\frac{g⋅D}{b}\right)⋅r}⋅3.6$$
Formel für den Radius r:
$$r=\frac{\left(\frac{v}{3.6}\right)^2}{a_q+\frac{g⋅D}{b}}$$
Formel für die Überhöhung D:
$$D=\left[\frac{\left(\frac{v}{3.6}\right)^2}{r}-a_q\right]⋅\frac{b}{g}$$
Formel für die freie Seitenbeschleunigung aq:
$$a_q=\frac{\left(\frac{v}{3.6}\right)^2}{r}-\frac{g⋅D}{b}$$
Haftreibungszahl relevant (Straßenverkehr)
Ist hingegen die Haftreibungszahl µ relevant, bekommt man die zulässige Geschwindigkeit v in Kurven mit der folgenden Formel:
$$v=\sqrt{\frac{µ+sin(\beta)}{1-sin(\beta)⋅µ}⋅g⋅r}⋅3.6$$
Formel für den Radius r:
$$r=\frac{\left(\frac{v}{3.6}\right)^2}{\frac{µ+sin(\beta)}{1-sin(\beta)⋅µ}⋅g}$$
Formel für die Überhöhung D:
$$D=\frac{\left(\frac{v}{3.6}\right)^2-µ⋅g⋅r}{\left(\frac{v}{3.6}\right)^2⋅µ+g⋅r}⋅b$$
Formel für die Haftreibungszahl µ:
$$µ=\frac{\left(\frac{v}{3.6}\right)^2-sin(\beta)⋅g⋅r}{\left(\frac{v}{3.6}\right)^2⋅sin(\beta)+g⋅r}$$
Formeln & Skizzen zur Berechnung der Winkel
Der Steigungswinkel und auch der Überhöhungswinkel kommen in vielen der Formeln vor, weshalb sie hier definiert werden. Für Umrechnungen zwischen Längen und Winkeln sei auch auf meinen Steigungsrechner hingewiesen!
Steigungswinkel α
Verläuft die Straße bzw. die Bahnstrecke eben oder nur mäßig steil, kann der Ausdruck cos(α) in allen Formeln gleich eins gesetzt werden. Der Steigungswinkel α einer Straße oder Bahnstrecke wird wie folgt berechnet:
$$\alpha=arctan\left(\frac{h}{a}\right)$$
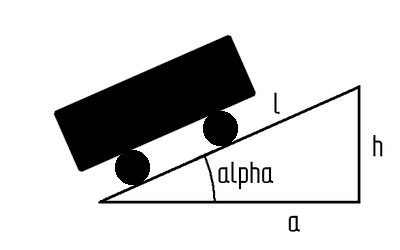
| a: | horizontaler (= waagrechter) Abstand |
| h: | Höhenunterschied (= vertikaler Abstand) |
| l: | Länge der Schrägen, also z. B. die Länge der Straße |
| α: |
Steigungswinkel; Winkel zwischen der Fahrbahn bzw. dem Gleis und der Horizontalen |
Überhöhungswinkel β
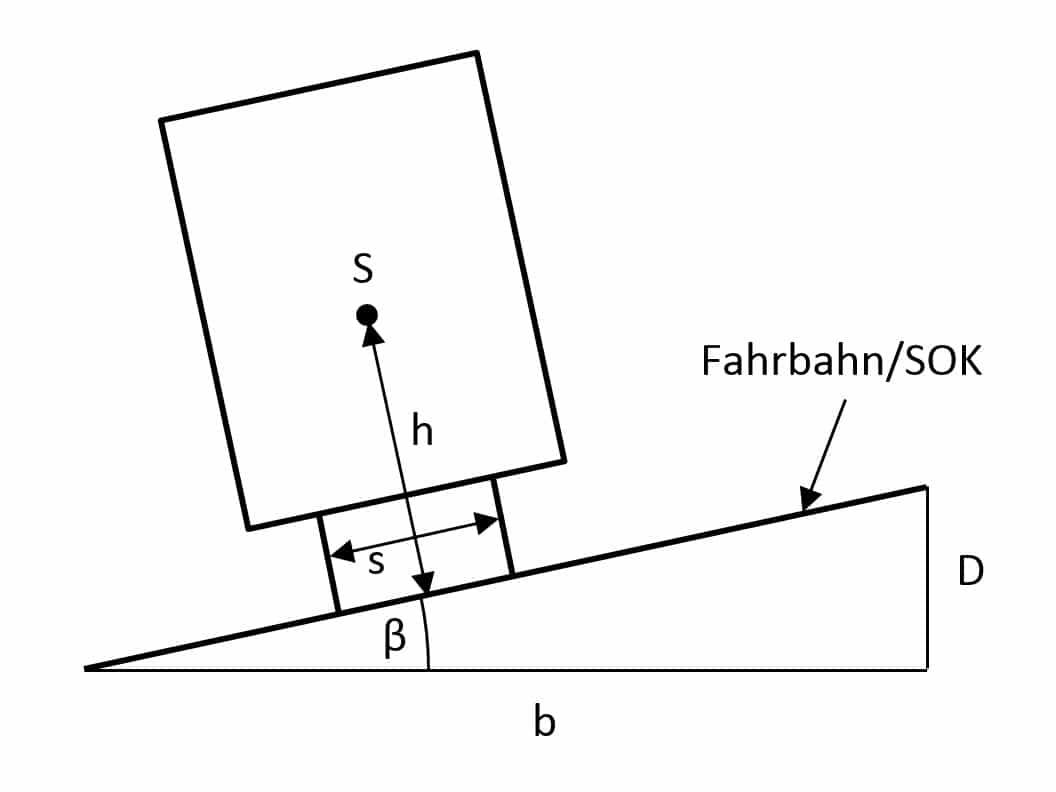
Der Überhöhungswinkel β beträgt:
$$\beta=arctan\left(\frac{D}{b}\right)$$
| D: | vertikaler Abstand = Überhöhung |
| b: | horizontaler Abstand |
| s: | Abstand zwischen den Radaufstandspunkten |
| β: |
Überhöhungswinkel |
Hinweise für die Eisenbahn
- Der Abstand s beträgt für eine Normalspurbahn (Spurweite 1435 mm) 1500 mm. Es gilt zudem: b ≈ s. Die Regelüberhöhung D lautet 160 mm. Eine stärkere Überhöhung ist nicht zulässig, da sonst die Gefahr eines Kippens nach innen besteht, falls einmal ein Zug in der überhöhten Kurve stehen bleiben oder langsam fahren muss. Auch wirkt sich eine sehr große Überhöhung negativ auf den Fahrgastkomfort aus, wenn es zum Stillstand des Zuges kommt.
- Für eine Gartenbahn mit der Spurweite 5 Zoll kann man für b und s ca. 130 mm annehmen. Der Gartenbahnbetrieb unterscheidet sich vom Vorbild: Eine Überhöhung ist wegen der geringen Geschwindigkeit meist nicht nötig (siehe Diagramme weiter unten). Aufgrund der relativ engen Radien und der mitunter hohen Schwerpunktlage der Fahrzeuge durch darauf sitzende Personen kann es leicht zum Kippen der Fahrzeuge kommen. Daher empfiehlt es sich, die Gleise maximal 5 mm (Spur 5) zu überhöhen, wobei die freie Seitenbeschleunigung einen Wert von 0.5 m/s² nicht überschreiten sollte.
- Bei Modelleisenbahnen wird meist auf eine Kurvenüberhöhung komplett verzichtet.
Exakte Formeln & Werte
Bei steilen Straßen und/oder bei großen Überhöhungen ist es nicht zulässig, den cos gleich eins zu setzen. Statt den vereinfachten Formeln sind die folgenden, exakten Formeln zu verwenden. Neben den Formeln findest du hier auch Werte für die freie Seitenbeschleunigung und für Kurvenradien.
Formeln mit freier Seitenbeschleunigung
Ist die zulässige freie Seitenbeschleunigung aq bekannt, was in der Regel auf Schienenfahrzeuge zutrifft, berechnet sich die zulässige Geschwindigkeit v in Kurven mit der folgenden Formel:
$$v=\sqrt{\left (\frac{a_q+g⋅sin(\beta)⋅cos(\alpha)}{cos(\beta)}\right)⋅r}⋅3.6$$
Man kann nun die obige Formel auf getrennten Nenner bringen und dann den allgemein gültigen Zusammenhang tan(β) = sin(β)/cos(β) verwenden. Mit der Formel tan(β) = D/b bekommt man schließlich:
$$v=\sqrt{\left (\frac{a_q}{cos(\beta)}+g⋅\frac{D}{b}⋅cos(\alpha)\right)⋅r}⋅3.6$$
In der folgenden Tabelle findet man typische Werte für die zulässige freie Seitenbeschleunigung auf Eisenbahnstrecken in Österreich:
| Beispiel | freie Seitenbeschleunigung in m/s² |
| Regelwert für Neubaustrecken | 0.65 |
| Maximalwert für existierende Strecken | 0.85 |
| Straßenbahn (straßenabhängig) | 1.00 * |
| Für Fahrzeuge mit Neigetechnik | ~ 2.00 |
* Quelle: RIS
Vergleichswerte für den Kurvenradius (Eisenbahn)
| Beispiel | Minimaler Radius in m |
Spurweite in mm |
| Straßenbahn Lissabon | 9 | 900 |
| Straßenbahn Salzburg | 15 | 1435 |
| Straßenbahn Graz | 17.5 | 1435 |
| Straßenbahn Wien | 20; in Ausnahmefällen nur 18 * | 1435 |
| Badner Bahn | 19.3 | 1435 |
| U-Bahn Wien: U2 | 100 (zw. Schottentor und Rathaus) | 1435 |
| U-Bahn Wien: U4 | 110 (bei Landstraße) | 1435 |
| U-Bahn Wien: U6 | 120 (bei Tscherttegasse) | 1435 |
| Ybbstalbahn (Regelbetrieb †) | 60 | 760 |
| Mariazellerbahn | 80 | 760 |
| Mühlkreisbahn | 112 | 1435 |
| Gutensteinerbahn | 139 | 1435 |
| Semmeringbahn | 190 | 1435 |
Quelle: Wikipedia
* Quelle: TU Wien, Institut für Eisenbahnwesen
Formeln mit der Haftreibungszahl
Ist hingegen die Haftreibungszahl µ von Bedeutung, was eigentlich nur bei Straßenfahrzeugen der Fall ist, berechnen sich die zulässige Geschwindigkeit v in Kurven und die benötigte Überhöhung D wie folgt:
$$v=\sqrt{\frac{cos(\beta)⋅µ+sin(\beta)}{cos(\beta)-sin(\beta)⋅µ}⋅g⋅r⋅cos(\alpha)}⋅3.6$$
$$D=\frac{\left(\frac{v}{3.6}\right)^2-µ⋅g⋅r⋅cos(\alpha)}{\left(\frac{v}{3.6}\right)^2⋅µ+g⋅r⋅cos(\alpha)}⋅b$$
Werbung
Seite erstellt am 25.09.2021. Zuletzt geändert am