Wie schnell kann man in eine Kurve fahren? Finden Sie es mit diesem Rechner heraus!
Eine der folgenden Größen können Sie mit diesem Online-Rechner bestimmen: maximal mögliche Geschwindigkeit bei einer Kurvenfahrt, Radius, Überhöhung oder Haftreibungszahl bzw. freie Seitenbeschleunigung. Der Rechner ist sowohl für Straßenfahrzeuge (Auto, LKW, Motorrad bzw. Fahrrad) als auch für Züge geeignet. Zudem wird berechnet, ob das Fahrzeug bei einer gegebenen Geschwindigkeit nach außen kippt. Dazu passendes Hintergrundwissen finden Sie im Anschluss, während die vom Rechner verwendeten Formeln auf einer eigenen Seite stehen:
Mit der Voreinstellung wird die maximal zulässige Geschwindigkeit eines PKW in einer nicht überhöhten Kurve mit einem Radius von 25 m berechnet, wobei die Fahrbahn als sauber und trocken angenommen wird.
Werbung
Rechner für maximal mögliche Geschwindigkeit in Kurven
Unter “Vorauswahl” findet man passende Werte für Straßen- und Eisenbahnfahrzeuge.
Achtung: Dabei ändern sich auch die Eingabefelder!
* Die Haftreibungszahl bzw. die freie Seitenbeschleunigung wird automatisch durch die Auswahl der Straßenbedingung bzw. der Streckenart eingetragen, sie kann jederzeit geändert werden. Die Seitenbeschleunigung aq kann auch negativ sein!
** Die Überhöhung D darf auch negativ sein! Oft ist statt b und D der Winkel bekannt; es gilt: tan(β) = D/b. Für Umrechnungen bei einem gegebenen Winkel sei auch auf meinen Steigungsrechner verwiesen.
*** Es ist die Steigung der Straße bzw. Bahnstrecke gemeint. Auch negative Werte sind möglich!
Was die verschiedenen Abkürzungen (D, b, s, h und γ) bedeuten, erfährt man im übernächsten Abschnitt: Skizzen und allgemeine Information.
Hinweise für die Verwendung des Rechners
- Dieses Berechnungsprogramm ist sowohl für Eisenbahnen als auch für alle Straßenfahrzeuge (Auto, LKW, Zweiräder) gedacht.
- Mit dem Rechner kann eine der folgenden Größen ermittelt werden:
- Notwendiger Radius (in Gleis- bzw. Fahrzeugmitte)
- Freie Seitenbeschleunigung (Schiene) bzw. Haftreibungszahl (Straße)
- Maximal zulässige Geschwindigkeit für verschiedene Bedingungen
- Nötige Überhöhung – für geringe Überhöhungen (Formel ist nur Näherung für kleine Winkel)
- Bei Zweirädern: Winkel zwischen Rad und Straße, da es hier keine freie Seitenbeschleunigung gibt.
- Außerdem wird berechnet, ob das Fahrzeug bei einer vorgegebenen Geschwindigkeit nach außen kippt – abhängig von der Lage des Schwerpunkts und vom Abstand zwischen den Radaufstandspunkten. Kippen nach innen aufgrund von starker Überhöhung und zu geringer Geschwindigkeit oder Stillstand kann noch nicht bestimmt werden!
- Folgende Dinge werden bei der Berechnung nicht berücksichtigt:
- Federn, Dämpfer, Reifen und dgl. – es wird das vereinfachte Modell eines starren Körpers angenommen!
- Seitenwind kann vor allem bei hohen Fahrzeugen von Bedeutung sein.
- Schienenfahrzeuge können zudem auf der Schiene aufklettern (Entgleisungskriterium nach Nadal).
- Bei unebener Fahrbahn und vor allem bei höherem Tempo werden die Räder eines Fahrzeuges zeitweise entlastet – zu diesen Zeitpunkten können folglich nur geringere Querkräfte übertragen werden.
- Beim Bremsen bzw. Beschleunigen in der Kurve ergibt sich eine kleinere zulässige Geschwindigkeit, da sich dann die für die Kurvenfahrt zur Verfügung stehende Haftreibungszahl verringert.
- Für die richtige Funktion wird keine Gewähr übernommen – für Berichtigungen und Verbesserungs-Vorschläge bitte um Nachricht mittels Kontaktformular!
Hintergrundwissen
Die vom Rechner verwendeten Formeln und auch typische Zahlenwerte für die freie Seitenbeschleunigung und für Kurvenradien bei Eisenbahnen sind auf einer eigenen Seite zu finden:
Bei diesem Rechner spielen die Haftreibungszahlen eine sehr wichtige Rolle. Ausführliche Informationen dazu gibt es auf dieser Unterseite:
Freie Seitenbeschleunigung
Die freie Seitenbeschleunigung aq multipliziert mit der Masse des Fahrgastes ergibt jene Kraft, die der Fahrgast bei einer Kurvenfahrt verspürt – sie drückt ihn in der Regel nach außen. Besonders bei langsamer Kurvenfahrt kann die freie Seitenbeschleunigung auch negativ sein.
Von einer ausgeglichenen Seitenbeschleunigung spricht man, wenn bei einer Kurvenfahrt keinerlei Kräfte auf die Fahrgäste wirken. Das ist allerdings – in Abhängigkeit von Kurvenradius und Überhöhung – immer nur für genau eine Geschwindigkeit möglich.
Skizzen und allgemeine Informationen
Die folgenden Abbildungen zeigen die Situation für einen Zug bzw. ein Kraftfahrzeug (PKW, LKW) und für einen Zweiradfahrer:
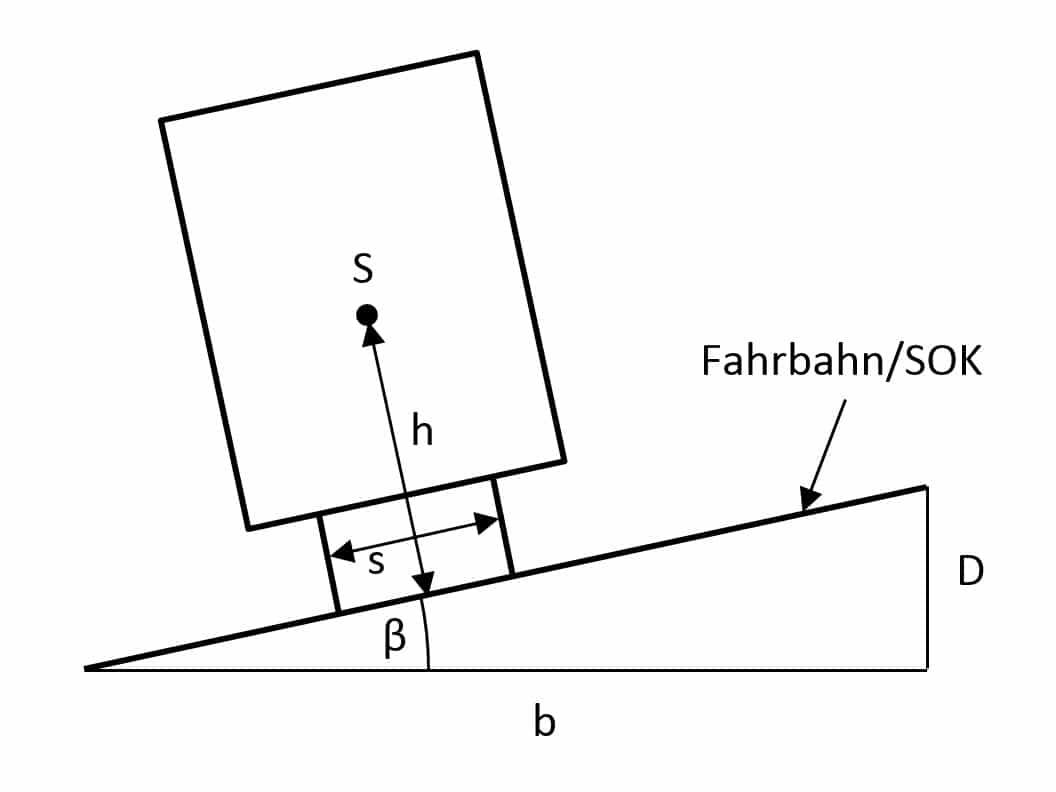
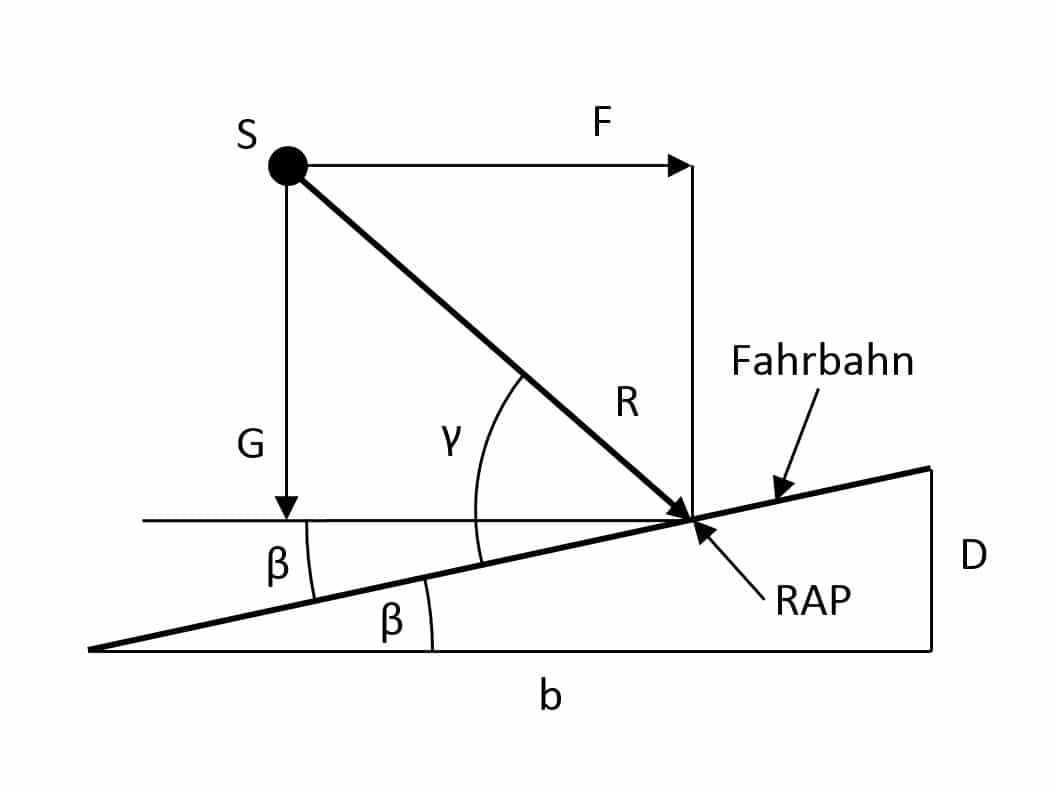
Erklärung der Abkürzungen
| F: | Fliehkraft |
| G: | Gewichtskraft |
| R: | Resultierende Kraft, geht bei Zweirad-fahrern stets durch den Radaufstandspunkt |
| S: | Schwerpunkt des Fahrzeugs |
| β: | Winkel der Kurvenüberhöhung |
| b: | horizontaler Abstand |
| D: |
vertikaler Abstand = Überhöhung; auch negative Werte sind möglich! |
| h: | Abstand Schwerpunkt – Fahrbahn bzw. SOK |
| s: | Abstand zwischen den Radaufstandspunkten |
| γ: | Winkel zwischen Zweirad & Fahrbahn |
| RAP: | Radaufstandspunkt |
| SOK: | Schienenoberkante |
Was man unter dem Steigungswinkel α versteht, zeigt die folgende Abbildung:
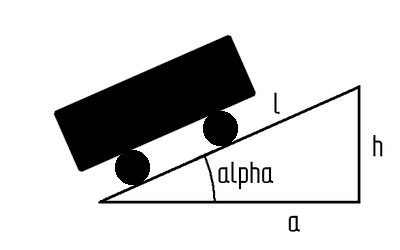
| a: | horizontaler (= waagrechter) Abstand |
| h: | Höhenunterschied (= vertikaler Abstand) |
| l: | Länge der Schrägen, also z. B. die Länge der Straße |
| α: |
Steigungswinkel; Winkel zwischen der Fahrbahn bzw. dem Gleis und der Horizontalen |
Für Umrechnungen von Winkel und Längen sei auch auf meinen Steigungsrechner verwiesen!
Diagramme – speziell für Gartenbahn & Straßenbahn
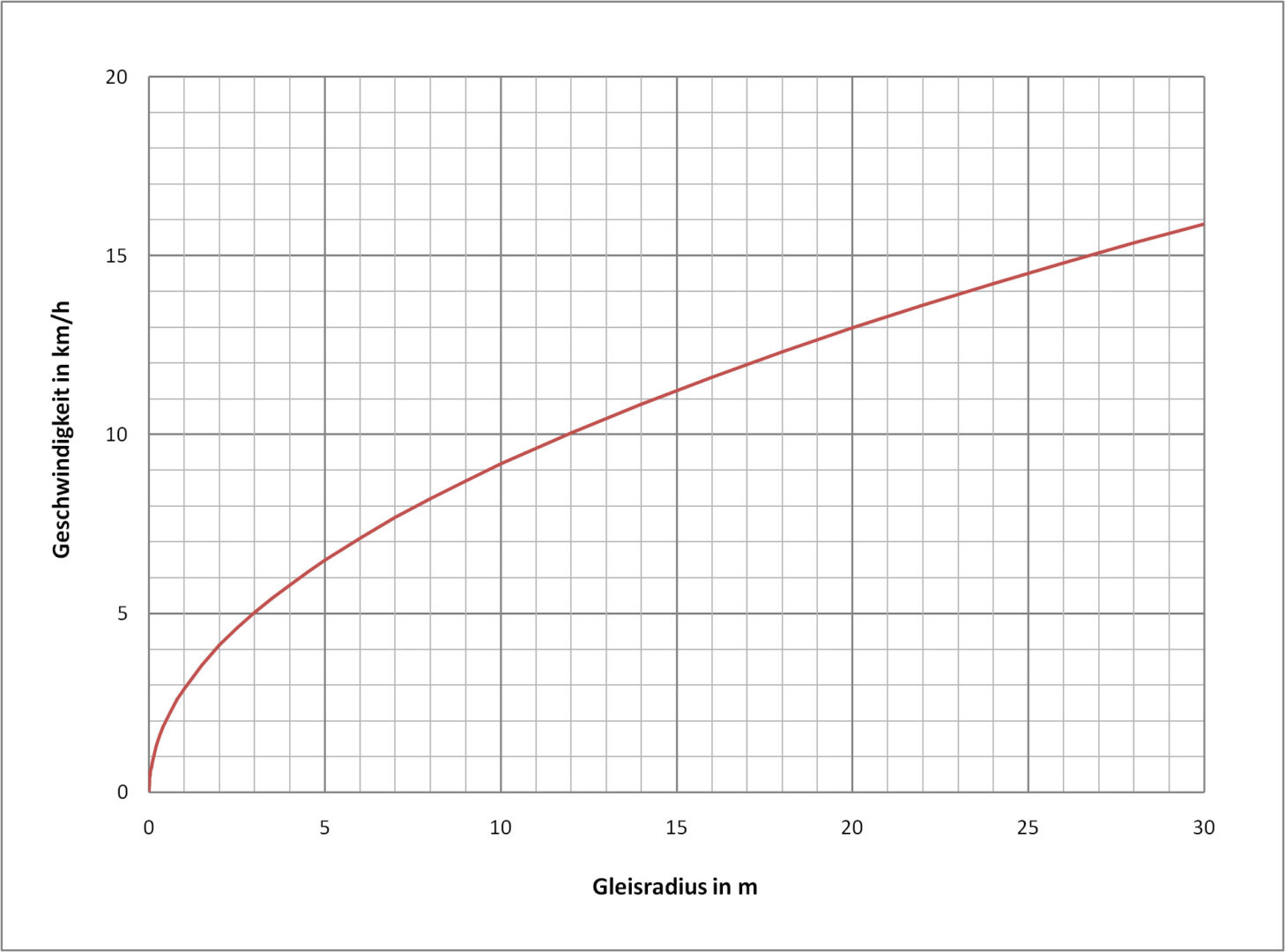
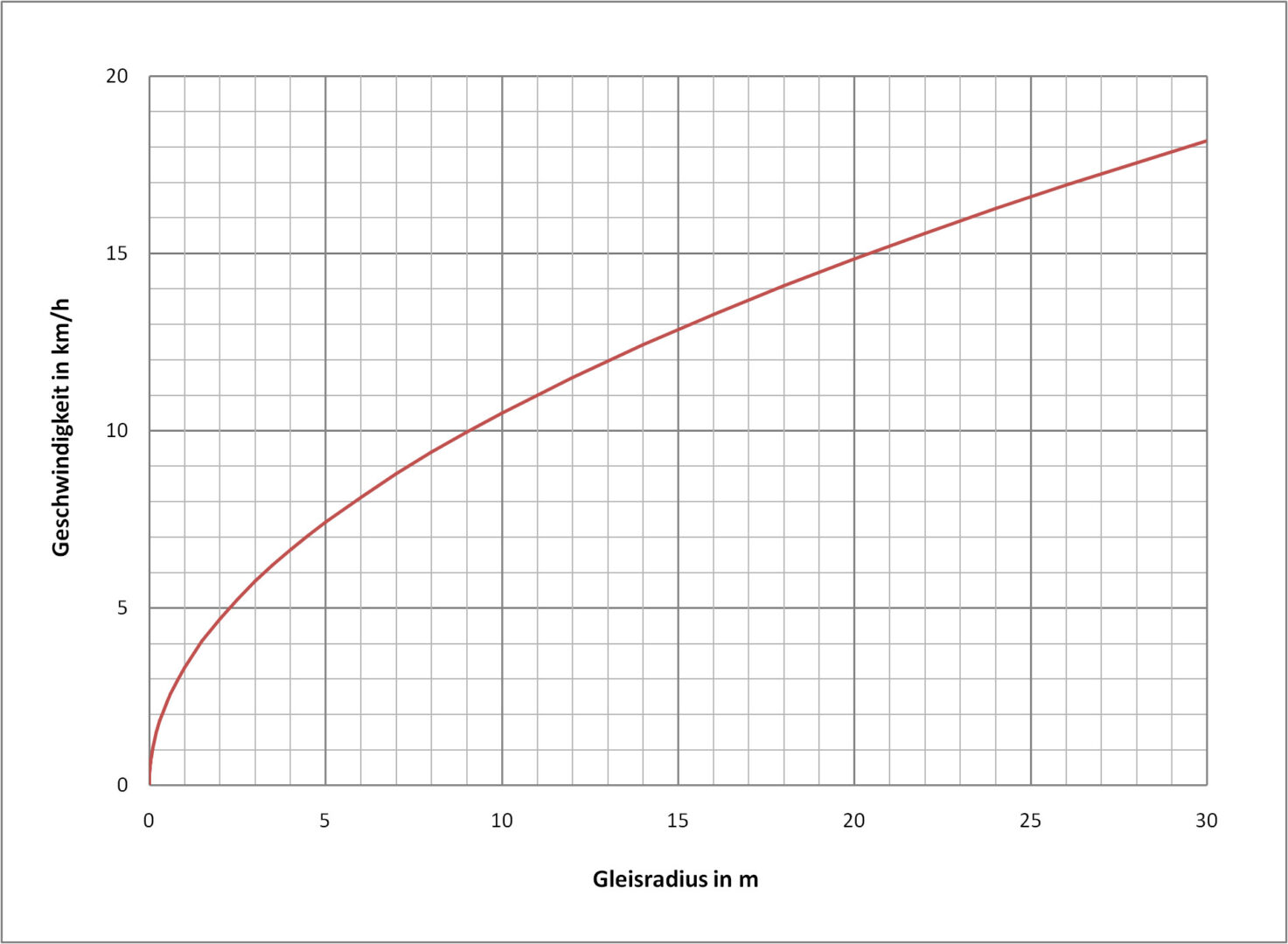
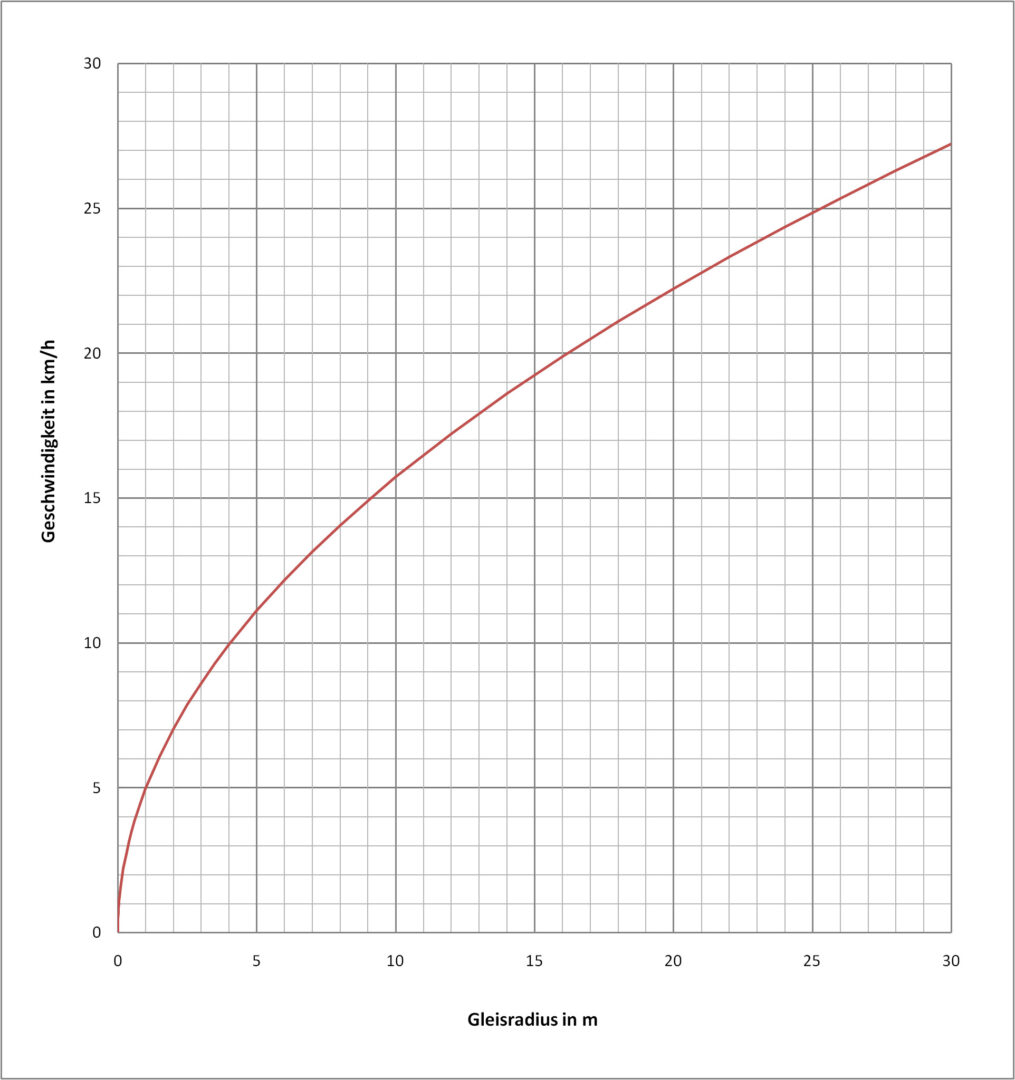
Die folgenden Diagramme zeigen die zulässige Geschwindigkeit in Kurven in Abhängigkeit vom Gleisradius. Aufgrund der engen Radien sind diese Diagramme nur für Gartenbahnen oder Straßenbahnen sinnvoll. Die freie Seitenbeschleunigung aq und die Überhöhung D variieren:
- Aus den ersten beiden Diagramme kann die erlaubte Kurvengeschwindigkeit bei einer freien Seitenbeschleunigung von 0.65 m/s² bzw. 0.85 m/s² abgelesen werden – die Überhöhung ist in beiden Fällen 0.
- Das letzte Diagramm zeigt die maximale Geschwindigkeit für eine 5 Zoll Gartenbahn, wenn die Seitenbeschleunigung 0.85 m/s² beträgt und das Gleis 14 mm überhöht wird – das entspricht einer Überhöhung von 162 mm bei einer Normalspurbahn.
Werbung
Seite zuletzt geändert am 08.03.2022.