This page in English: Calculator for Axial & Polar Area Moment of Inertia and Section Modulus
Dieser Online-Rechner berechnet die polaren und axialen Widerstands- & Flächenträgheitsmomente (auch als Flächenmomente 2. Grades bezeichnet), die Randfaserabstände und die Querschnittsfläche verschiedener Holz- oder Stahlprofile. Von vielen kreisförmigen und dünnwandigen Profilen können auch die Torsionsträgheitsmomente und die Torsionswiderstandsmomente ermittelt werden. Zudem kann man bei Bedarf die Masse eines Trägers bestimmen. Als Werkstoff stehen Stahl, Aluminium und unterschiedliche Holzarten zur Auswahl.
Links zu Unterseiten:
- Formeln für die axialen/polaren Widerstandsmomente und Flächenträgheitsmomente
- Theorie, Beispiele & Herleitung der Formeln zur Berechnung des Flächenträgheitsmoments
Werbung
Flächenträgheitsmoment- & Widerstandsmoment-Rechner
Mit der Voreinstellung können Sie die (Flächen-)Trägheitsmomente, die Widerstandsmomente, die Masse und den Flächeninhalt für einen idealisierten I-Träger (I100) berechnen.
* Diese beiden Felder sind nur dann auszufüllen, wenn auch die Masse berechnet werden soll, da die Trägheitsmomente und die Widerstandsmomente geometrische Größen und daher vom gewählten Werkstoff unabhängig sind!
Es wird immer das kleinste Widerstandsmoment ausgegeben! Die Berechnung erfolgt für idealisierte Profile, das heißt, schräge Kanten und Abrundungen können nicht berücksichtigt werden!
Erklärung der Abkürzungen
| Dm | Durchmesser in mm |
| Iy, Iz | axiale Flächenträgheitsmomente |
| Wy, Wz | Widerstandsmomente |
| It | Torsionsträgheitsmoment |
| Wt | Torsionswiderstandsmoment |
| Ip | polares Flächenträgheitsmoment: Ip = Iy + Iz für kreisförmige Querschnitte gilt: It = Ip |
| e1-4 | Randfaserabstände, siehe folgender Abschnitt |
Randfaserabstände
Der Randfaserabstand ist der Abstand von der neutralen Faser zur Randfaser. Die neutrale Faser verläuft bei homogenen Querschnitten stets durch den Schwerpunkt SP der Fläche, der in der Mitte des Koordinatensystems liegt. Die 4 Randfasern (= Querschnittsrand) sind von den jeweiligen Koordinatenachsen am weitesten entfernt.
Die Skizze zeigt an vier Beispielen, welche Längen die Randfaserabstände e1, e2, e3 und e4 bezeichnen. Die Längen e1 und e2 sind also die vertikalen Randfaserabstände und die Längen e3 und e4 entsprechen den horizontalen Randfaserabständen
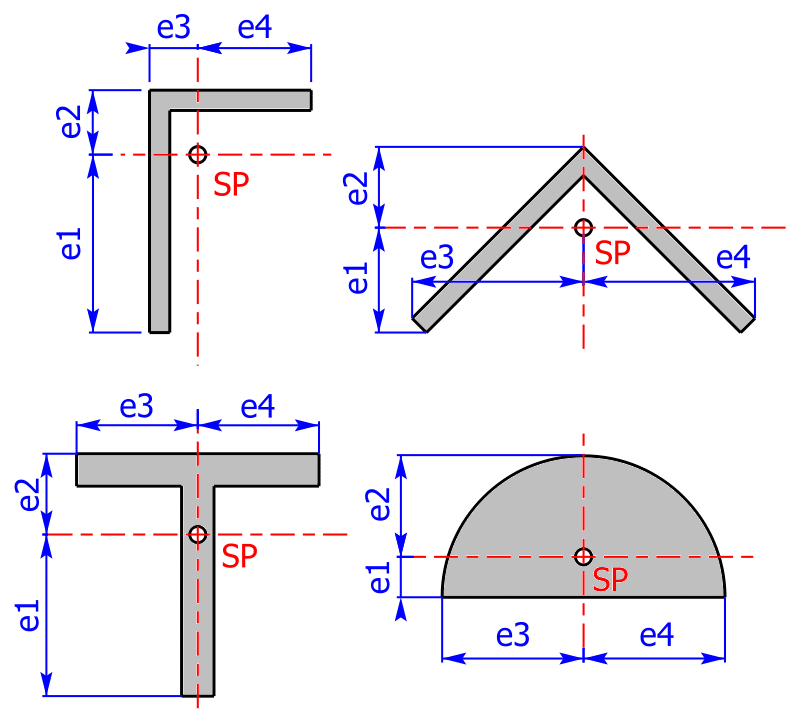
Ist der Querschnitt bezüglich einer Achse nicht symmetrisch und folglich e1 ≠ e2 und/oder e3 ≠ e4, gibt es zwei unterschiedliche Widerstandsmomente um diese Achse! Der Rechner gibt stets das kleinere der beiden Widerstandsmomente aus.
Hinweise für die Verwendung des Rechners
- Folgende Querschnitte sind verfügbar, wobei die mit * bezeichneten Profile auch ein Durchgangsloch bzw. eine Bohrung besitzen können:
- Rundstange (Kreis), auch mit Passfedernut *
- Rundrohr (Kreisring)
- Halb-Rundstab (Halbkreis)
- Rechteck-Profil *
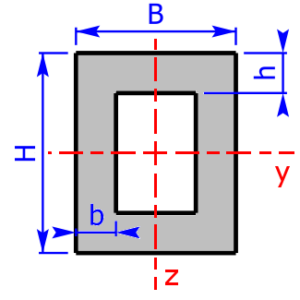
- Rechteck-Hohlprofil / Formrohr / Vierkantrohr *
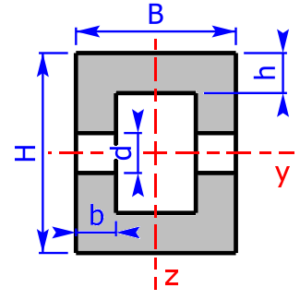
- Rechteck mit Bohrung
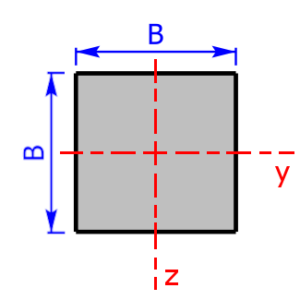
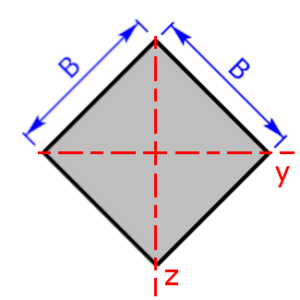
- Quadrat / Quadrat um 45 Grad gedreht
- I- bzw. H-Profil (Doppel-T-Träger) *
- U- bzw. C-Profil *
- T-Profil
- L-Profil (Winkelprofil), gleich- und ungleichschenkelig
- L-Profil (gleichschenkelig) um 45° gedreht
- Gleichschenkeliges / gleichseitiges Dreieck
- Sechseck / Sechskant
- Achteck / Achtkant
- Weiter unten findet man Skizzen von allen Querschnittsprofilen. Die Querschnitte müssen immer symmetrisch zu den beiden Koordinatenachsen sein.
- Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular!
Hintergrundwissen zum Rechner
Die vom Rechner verwendeten Formeln bzw. deren Herleitungen findet man auf folgenden Unterseiten:
Vergleich: idealisiertes Modell und reales I-Profil I100
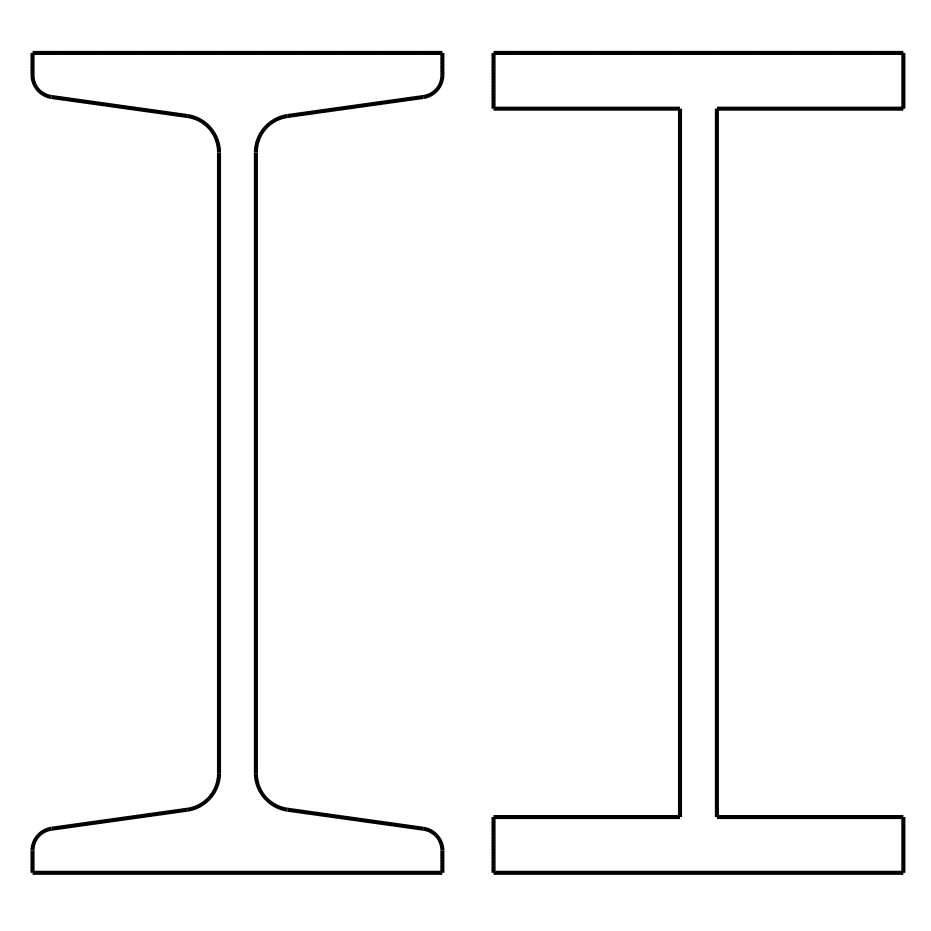
In der Abbildung sieht man einen schmalen I-Träger I100 und ein vereinfachtes Modell, wie es der Flächenträgheitsmomentrechner verwendet.
Die Abweichungen bei der Berechnung entstehen also dadurch, dass der reale I-Träger schräge Flanschflächen besitzt und die inneren Kanten abgerundet sind, wie man sehr gut in der Graphik erkennen kann.
Alle Zeichnungen wurden übrigens mit den beiden frei nutzbaren Programmen FreeCAD bzw. GIMP erstellt.
Die folgende Tabelle vergleicht die mit dem Rechner bestimmten und die realen Werte:
| Iy in cm4 |
Wy in cm3 |
Iz in cm4 |
Wz in cm3 |
A in mm2 |
m’ in kg/m |
|
| mit Rechner bestimmt | 172.1 | 34.4 | 14.2 | 5.7 | 1069 | 8.40 |
| tatsächliche Werte | 171 | 34.2 | 12.2 | 4.88 | 1060 | 8.34 |
| Abweichungen in % | 0.64 | 0.58 | 16.4 | 16.8 | 0.85 | 0.72 |
Wie man sieht, stimmen Iy und Wy, die Querschnittsfläche A und die Masse pro Meter sehr gut überein. Die z-Werte unterscheiden sich etwas mehr, sind aber durchaus als Abschätzung noch brauchbar.
Anmerkungen:
- I-Träger werden z. B. bei Brücken immer hochkant eingebaut, da sie in dieser Lage wesentlich höher belastbar sind, man vgl. Wy mit Wz. Gerade bei diesem in der Praxis meist relevanten Wert Wy stimmt die Berechnung sehr gut mit der Realität überein!
- Ähnliches gilt natürlich auch für die anderen Profile.
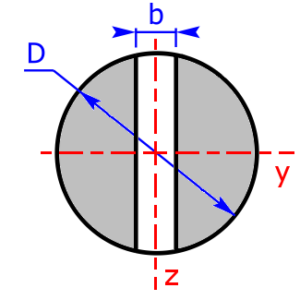
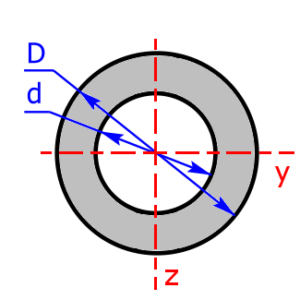
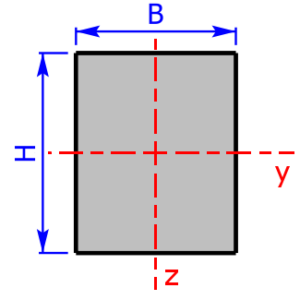
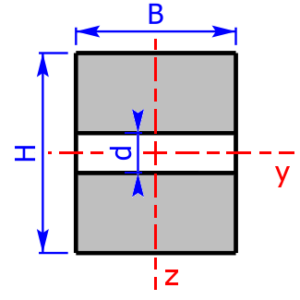
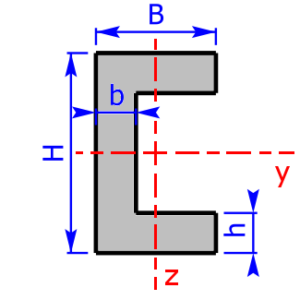
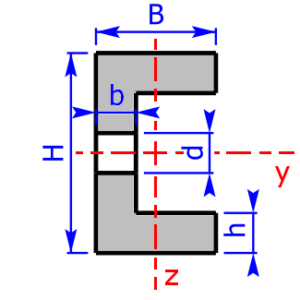
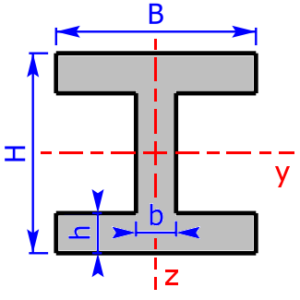
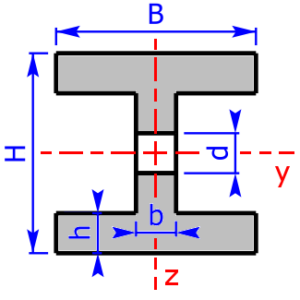
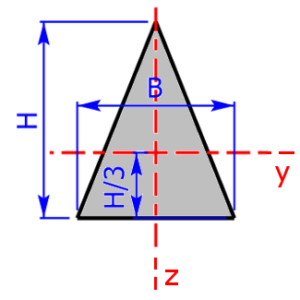
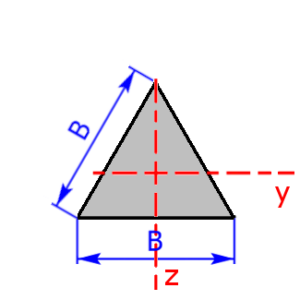
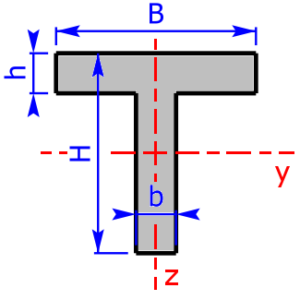
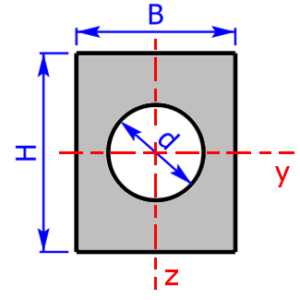
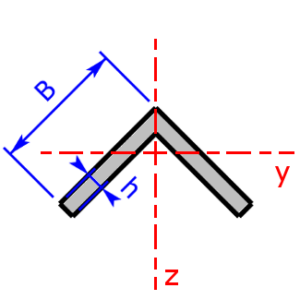
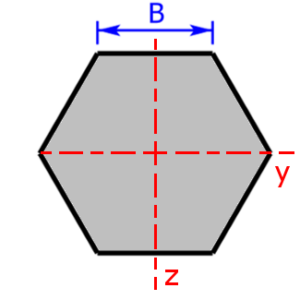
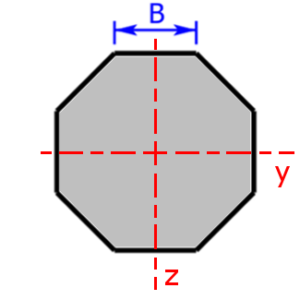
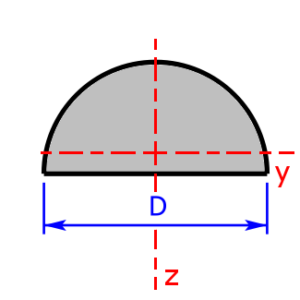
Skizzen der verfügbaren Querschnittsprofile
Die folgenden 23 Profile können beim Rechner als Querschnitt ausgewählt werden. Die Formeln zur Berechnung findet man auf einer eigenen Seite:
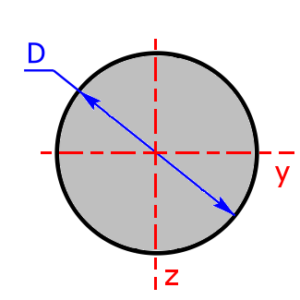
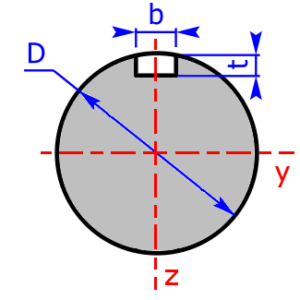

Werbung
Seite erstellt im März 2018. Zuletzt geändert am: