Stützt sich ein starrer Körper auf vier Punkten ab (= Vierpunktstützung), handelt es sich im Prinzip um ein einfach statisch unbestimmtes System und es müssten daher auch die Verformungen berücksichtigt werden.
Falls jedoch die Rahmenkonstruktion teilweise nachgiebig ist bzw. die Abstützung gefedert erfolgt und/oder die Belastung relativ hoch ist, sodass an allen vier Stellen guter Kontakt zum Boden herrscht, können die Auflagerkräfte mit diesem Online-Rechner näherungsweise berechnet werden. Die vom Rechner verwendeten Formeln findet man am Ende der Seite.
Werbung
Skizze & Rechner zur Ermittlung der Auflagerkräfte
Die mit A, B, C und D beschrifteten Kreise bezeichnen die vier Auflager und können z. B. Räder oder Tischbeine symbolisieren (Draufsicht). Der Koordinatenursprung befindet sich genau in der Mitte des Rechtecks, das heißt, alle vier Punkte sind gleich weit davon entfernt. Die Berechnung erfolgt näherungsweise für relativ nachgiebige Konstruktionen bzw. für hohe Belastungen:
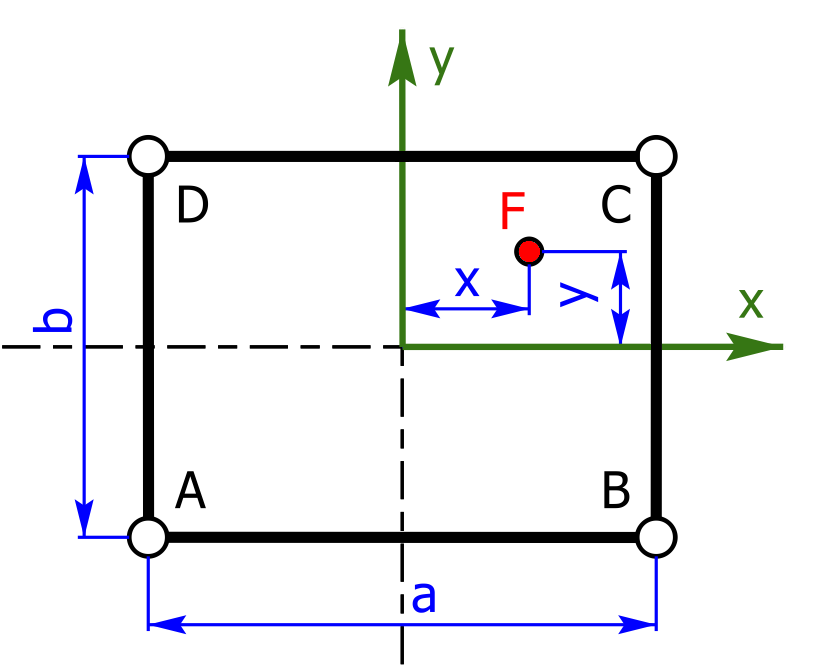
* Die Abstände x und y können je nach Lage von der Belastung F auch negative Werte annehmen. Zudem ist es möglich, dass x oder y größer als a/2 bzw. b/2 ist – das heißt, die Belastung kann sich auch außerhalb des Rahmens befinden! In diesem Fall werden zwei der Auflagerkräfte negativ, da sie nun in die andere Richtung wirken. Ein Abheben vom Boden muss z. B. durch eine Verschraubung vermieden werden.
Anmerkungen
- Ein kleiner, unbelasteter Tisch wird fast immer wackeln, da meist nur drei der vier Beine Bodenkontakt haben. In diesem Fall ist die Berechnung mit diesem Rechner auf jeden Fall unzulässig!
- Vorsicht ist auch bei einem unebenen Boden geboten, da in diesem Fall eine gute Vierpunktauflage oft nicht möglich ist.
- Statt Kilogramm (kg) kann man natürlich auch Newton (N), Kilonewton (kN), Tonnen (t) oder eine andere Einheit benützen: Jene Einheit, die für die Last F verwendet wird, kommt für die vier Aufstandskräfte heraus. Das kann man gut erkennen, wenn man sich die vom Rechner verwendeten Formeln ansieht.
- Ähnliches gilt für die Abstände: Hier kann jede beliebige Längenmaßeinheit benützt werden, aber natürlich muss man für die vier Längen a, b, x und y dieselbe Einheit verwenden!
- Gibt man F = 100 kN ein (= Voreinstellung), erhält man die Verteilung der Belastung auf die vier Stützpunkte in % von F.
- Wirken mehrere Belastungen (z.b. Eigenwicht des Tisches und eine Last) gleichzeitig, können die gesamten Auflagerkräfte durch Superposition bestimmt werden.
- Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular.
Anwendungsbeispiele
- Berechnung der Radlasten von Kranfahrwerken oder Katzfahrwerken bei außermittiger Last. Dafür sind die vom Rechner verwendeten Formeln prinzipiell vorgesehen.
- Ermittlung der Radlasten eines Autos oder eines vierachsigen Anhängers bei symmetrischer und insbesondere unsymmetrischer Beladung. Zur Ermittlung der Achslast müssen noch die berechneten Radlasten der beiden Hinterräder und der zwei Vorderräder addiert werden.
- Berechnung der Auflagerkräfte eines Tisches mit vier Beinen, der relativ stark belastet wird und dessen Platte nicht allzu steif ist. Es ist stets sicherzustellen, dass alle vier Beine (guten) Bodenkontakt haben.
Beispiel: Person steht auf Tisch mit vier Beinen
Auf der Unterseite Superposition findet man ein vollständig durchgerechnetes Beispiel: Eine Person steht auf einem Tisch mit vier Beinen, die Auflagerkräfte in den Aufstandspunkten sind gesucht. Zur Lösung dieser Aufgabe wird auch dieser Rechner verwendet.
Formeln für die Auflagerkräfte bei Vierpunkt-Stützung
Die folgenden Formeln werden zur Ermittlung der Auflagerkräfte in den Punkten A bis D vom Rechner verwendet und lauten:
$$A=F·\frac{\frac{a}{2}-x}{a}· \frac{\frac{b}{2}-y}{b}$$
$$B=F·\frac{\frac{a}{2}+x}{a}· \frac{\frac{b}{2}-y}{b}$$
$$C=F·\frac{\frac{a}{2}+x}{a}· \frac{\frac{b}{2}+y}{b}$$
$$D=F·\frac{\frac{a}{2}-x}{a}· \frac{\frac{b}{2}+y}{b}$$
Herleitung der Formel für die Auflagerkraft in C
Zur näherungsweisen Berechnung der Auflagerkräfte in den Punkten A, B, C und D erstellt man ein Modell, das aus drei Balken besteht:
Balken I stützt sich auf die Lager P und Q ab. Diese Lager sind als Fest- bzw. Loslager ausgeführt, sodass es sich um drei statisch bestimmte Teilsysteme handelt.
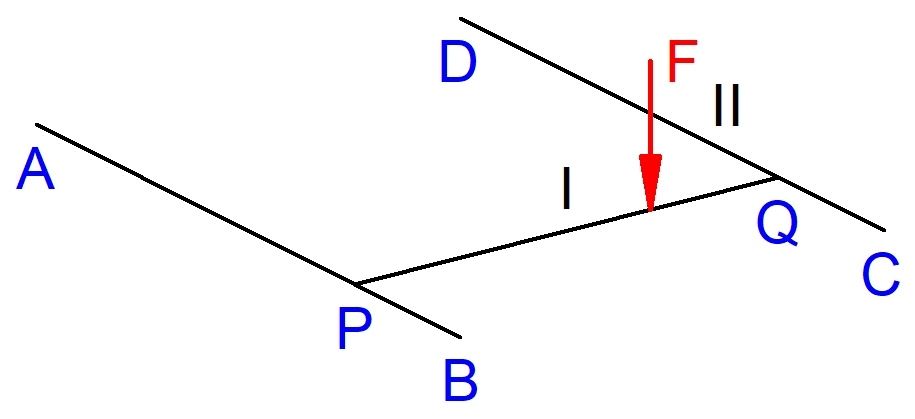
Zunächst sieht man sich Balken I an und berechnet die Auflagerkraft in Q. Dazu bildet man die Summe der Momente um P:
$$\sum M_P=0=-F·\left(\frac{b}{2}+y\right)+Q·b$$
$$\Rightarrow Q= F· \frac{\frac{b}{2}+y}{b}$$
Dann betrachtet man Balken II und schreibt die Summe der Momente bezüglich D an. Auf diese Weise bekommt man die Kraft C:
$$\sum M_D=0=+Q·\left(\frac{a}{2}+x\right)-C·a$$
$$\Rightarrow C= Q· \frac{\frac{a}{2}+x}{a}$$
Zuletzt setzt man für Q den schon zuvor berechneten Ausdruck ein und erhält die gesuchte Auflagerkraft in C:
$$\Rightarrow C= F · \frac{\frac{b}{2}+y}{b} · \frac{\frac{a}{2}+x}{a}$$
Ähnlich geht man bei der Berechnung der anderen Auflagerkräfte vor.
Werbung
Seite erstellt im Mai 2019. Zuletzt geändert am 15.09.2022.