Formeln für Knicken von Stäben (Euler & Tetmajer)

This page in English: Buckling of Columns (calculator and formulas)

Hier wird anhand eines allgemeinen Bei­spiels be­schrieben, welche Schritte bzw. Formeln nötig sind, um die Sicherheit gegen Knicken berechnen zu können, wenn die Last und die Quer­schnitts­form bekannt sind. Es sind die vier klas­sischen Euler­fälle zu berück­sichtigen, wobei ent­weder nach Tet­majer (unelas­tischer Bereich) oder Euler (Hooke­scher bzw. elas­tischer Bereich) gerechnet wird. Benötigte Werte findet man in Tabellen.


Link zu Unterseite:

Werbung

Wie geht man bei der Be­rech­nung gegen Knicken vor?

In den folgenden Ab­schnitten werden alle benötigten Formeln zur Berechnung dieser Größen ange­geben:

  • Knicklänge lk
  • Knick­spannung σK
  • Schlank­heits­grad λ
  • Grenz­schlankheit λg
  • Knick­druck­kraft FK
  • Knick­sicher­heit S

Die vier Eulerfälle – Faktor β zur Berech­nung der Knick­länge lk

Zuerst muss man ent­scheiden, welcher der vier Euler­fälle vor­liegt. Das folgende Bild zeigt die vier Euler­schen Knick­fälle, wobei der dazu­gehörende Faktor β ange­geben wird. Die roten Pfeile stellen dabei die Kraft F dar:
 

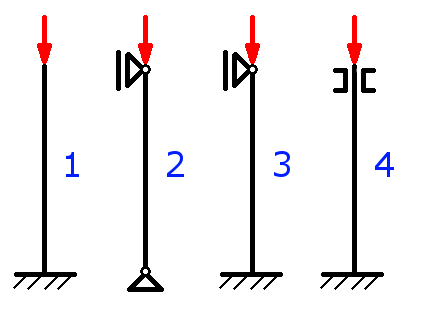
Die vier Eulerschen Knickfälle
Die vier Eulerschen Knickfälle
  • Fall 1: Der Stab ist am Boden fest ein­ge­spannt und das obere Ende ist kom­plett frei beweg­lich. Für diese Anord­nung gilt: β = 2.
  • Fall 2: Am unteren Ende befindet sich ein Fest­lager, oben ein Los­lager: β = 1. Das ist der in Praxis am häufig­sten vor­kom­mende Fall.
  • Fall 3: Am Boden wird der Stab fest ein­ge­spannt, während oben ein Los­lager ver­wendet wird. Hier gilt: β = 0.699.
  • Fall 4: Auch hier befindet sich unten eine feste Ein­span­nung. Das obere Ende wird hin­gegen in einem Längs­schlitz ge­führt: β = 0.5.


Die Knick­länge lk wird durch Multi­pli­kation von Faktor β und Stab­länge l berech­net. Es gilt also der folgende Zusammen­hang:

$$l_k=\beta·l$$

l Länge des Stabes in mm
β Faktor zur Berechnung von lk


Abhängig von den Lagerungs­bedin­gungen ergeben sich daher unter­schied­liche Knick­längen.

Formel für Schlankheitsgrad λ

Zunächst berechnet man sich den Schlank­heits­grad λ, wobei neben den schon bekannten Größen auch die Fläche und das kleinste Flächen­träg­heits­moment des Stabes benötigt werden:

$$\lambda=\sqrt{\frac{A}{I_{min}}}·\beta · l= \sqrt{\frac{A}{I_{min}}} · l_k $$

A Querschnittsfläche des Stabes in mm2
Imin Kleinstes axiales Flächenträgheitsmoment in mm4


Der Schlankheits­grad λ ist eine dimen­sions­lose Größe (korrekt: Größe der Dimension 1) und wird daher nur als Zahlen­wert ohne Ein­heit ange­geben.

Formel & Tabelle für Grenzschlankheit

Die Grenz­schlankheit λg des verwendeten Werk­stoffes kann mit der nächsten Formel bestimmt werden:

$$\lambda_g=\pi · \sqrt{\frac{E}{0.8 · R_{p0.2}}}$$

E E-Modul in N/mm²
Rp0.2 Elastizitätsgrenze/Fließgrenze bzw. Streck­grenze in N/mm²


Durch Einsetzen der werk­stoff­spezifischen Werte in die obige Formel erhält man die in der folgenden Tabelle zu findenden Grenz­schlank­heiten λg für die wichtigsten Werk­stoffe. Zusätz­lich wird auch die Streck­grenze ange­geben:

 

 Werkstoff Grenz­schlankheit λg Streckgrenze Rp0.2
 S235 (früher St37) 105 235
 S355 (früher St52) 85 355
 Grauguss (EN-GJL-200) 80* /
 Fichtenholz 100*  


* Hinweis:

Besitzt ein Werkstoff keine Streck­grenze, kann die Grenz­schlank­heit alter­nativ durch Gleich­setzen der Knick­spannungen nach Euler und Tet­majer bestimmt werden (Schneiden von zwei Funk­tionen).

Diagramm für Knick­span­nung in Abhängigkeit von λ

Falls der berechnete Schlank­heits­grad λ über der Grenz­schlank­heit λg liegt, wird nach Euler (Hooke­scher bzw. elas­tischer Bereich), andern­falls nach Tetmajer (unelas­tischer Bereich) gerechnet.

Liegt der Schlankheits­grad hin­gegen unter λp, spricht man von quetschen. Es handelt sich dann um kein Stabili­täts­problem, da in diesem Fall die Knick­spannung größer als die Streck­grenze ist, der Werk­stoff in der Regel (vor allem im Maschinen­bau!) aber nicht über die Streck­grenze be­lastet werden darf. Wie man die Quetsch­grenze λp be­rechnet, findet man etwas weiter unten auf dieser Seite.

Schlankheitsgrad-Knick­spannung-Dia­gramm für S235

Im folgenden Dia­gramm ist der Zusammen­hang zwischen dem Schlank­heits­grad λ und der Knick­spannung σK für den Bau­stahl S235 darge­stellt:
 

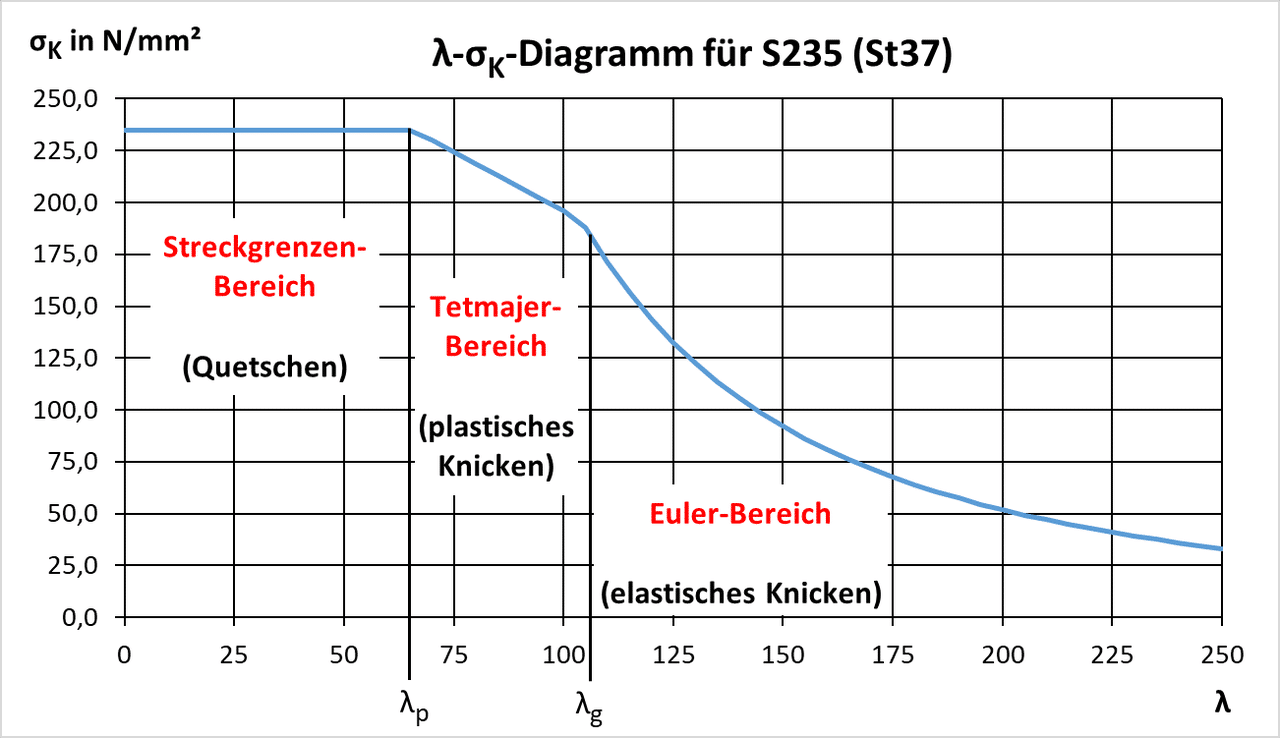
Schlankheitsgrad-Knickspannung-Diagramm (Baustahl S235 bzw. St37)
Schlankheitsgrad-Knickspannung-Diagramm (Baustahl S235 bzw. St37)

Schlankheitsgrad-Knick­spannung-Dia­gramm für S355

Für den Baustahl S355 sieht dieses Dia­gramm recht ähn­lich aus, wobei es in diesem Fall jedoch keinen Streck­grenzen-Bereich gibt, da die Knick­spannung σK stets unter­halb der Streck­grenze von 355 N/mm2 liegt:
 

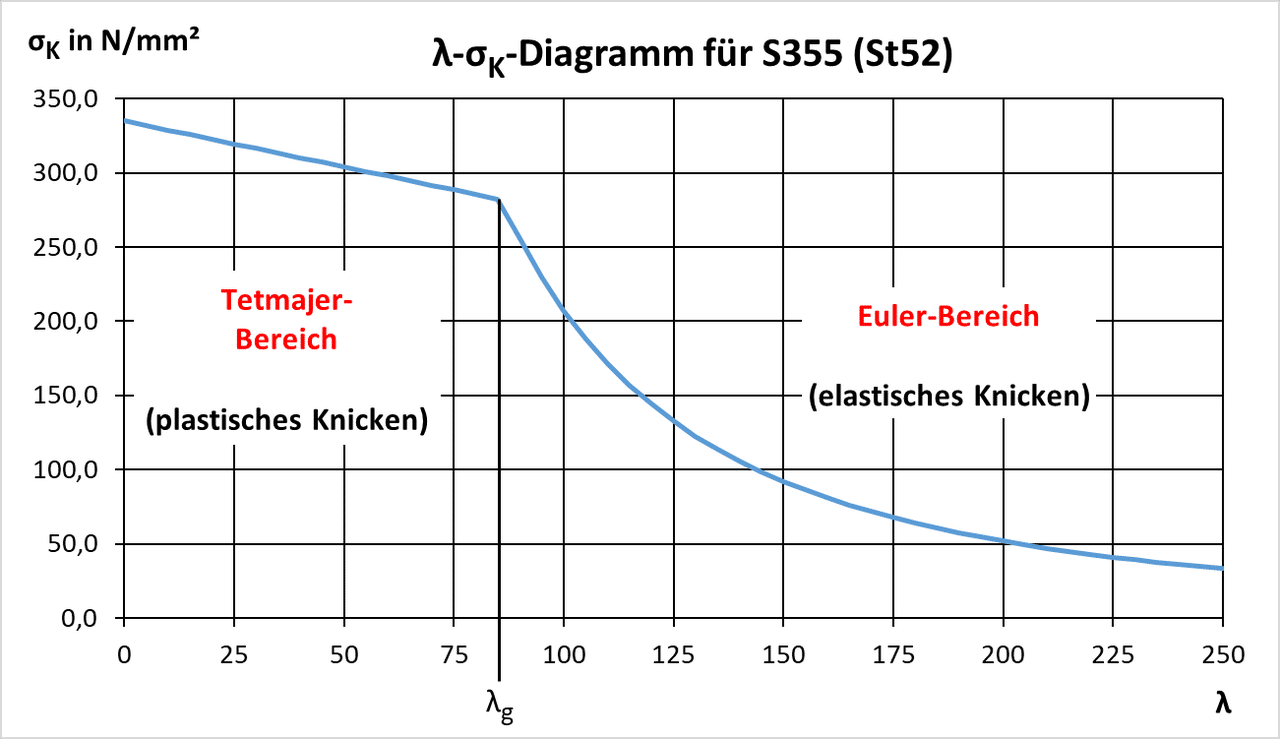
Schlankheitsgrad-Knickspannung-Diagramm (Baustahl S355 bzw. St52)
Schlankheitsgrad-Knickspannung-Diagramm (Baustahl S355 bzw. St52)

Formeln für Knick­span­nung & Knick­druck­kraft (Knick­last)

Die Formeln für die Knick­spannung σK und für die Knick­druck­kraft FK (= Knicklast) lauten:

Streckgrenze

Konstante

0 < λ < λp

$$σ_K > σ_{max} = R_{p0.2}$$

$$F_K > F_{max}=σ_{max}·A$$

Die Knick­spannung liegt über der Streck­grenze, somit liegt kein Stabili­täts­problem vor! Es handelt sich hier um quetschen.

Tetmajer (unelastischer Bereich)

Tetmajer-Gerade

λp < λ < λg

$$\sigma_K=a+b·\lambda+c · \lambda^2$$

$$F_K=(a+b·\lambda+c · \lambda^2) · A$$

Euler (elastischer Bereich)

Euler-Hyperbel

λg < λ < λmax = 250

$$\sigma_K=\frac{\pi^2 · E}{\lambda^2}= \frac{\pi^2 · E · I_{min}}{l_k^2 · A} $$

$$F_K= \frac{\pi^2 · E · I_{min}}{l_k^2} $$

 
λp, λg Grenzwerte; Formeln zur Berechnung und Tabellen siehe weiter oben bzw. unten!
λ Schlankheitsgrad
σK Druckspannung, bei der der Stab seitlich ausknickt; in N/mm²
FK Kraft, bei der der Stab seitlich ausknickt; in kN
Rp0.2 Elastizitätsgrenze bzw. Streck­grenze in N/mm²
σmax Üblicherweise maximal zulässige Spannung
E E-Modul in N/mm²; passende Werte findet man z. B. in Wikipedia
lk = β · l Knicklänge
β Faktor aufgrund der Lagerung des Stabes
l Länge des Stabes in mm
Imin Kleinstes axiales Flächenträgheitsmoment in mm4
A Querschnittsfläche des Stabes in mm²
a, b, c Koeffizienten für die Tetmajer-Gleichung


Achtung:

Im Euler-Bereich knicken bei identer Lagerung und Quer­schnitts­form alle Stähle unter der­gleichen Last, da sie den­selben E-Modul besitzen!

Tabelle mit Werten für die Koeffizienten der Tetmajer­gleichung

(negative Vor­zeichen von b be­achten!)
 

 Werkstoff Koeffizient a Koeffizient b Koeffizient c
 S235 (früher St37) 310 -1.14 0
 S355 (früher St52) 335 -0.62 0
 Grauguss 776 -12.0 0.053
 Fichtenholz 29.3 -0.194 0

Quelle: Wikipedia

Berechnung der Quetschgrenze λp

Im oberen Dia­gramm für den Stahl S235 ist auch eine Quetsch­grenze λp ein­ge­zeichnet. Diesen Wert bekommt man, indem man die Knick­spannung nach Tet­majer gleich der Streck­grenze Rp0.2 setzt und danach diese Gleichung um­formt:

$$\lambda_p=\frac{a-R_{p0.2}}{-b}$$

Das sei hier für den Bau­stahl S235 ge­zeigt:

$$R_{p0.2}=a+b · \lambda\Rightarrow235=310-1.14 · \lambda$$

$$\Rightarrow310-235=1.14 · \lambda\Rightarrow\frac{310-235}{1.14}=\lambda$$

$$\Rightarrow\lambda_p=65.79$$

 

 Werkstoff Grenze λp
 S235 (früher St37) 65.8
 S355 (früher St52) /


Für den Bau­stahl S355 existiert keine Quetsch­grenze, weil sich die Knick­spannung immer unter­halb der Streck­grenze befindet!

Sicherheit gegen Knicken

Zuletzt wird die Knicksicher­heit S berechnet:

$$S=\frac{F_K}{F}$$

FK Kraft, bei der der Stab seitlich ausknickt; in kN
F gegebene Kraft in kN


Es sind immer relativ große Sicher­heiten einzu­planen, da die Berech­nungen eigent­lich nur für einen idealen Stab gelten:

  • Der Stab muss homogen sein.
  • Die Kraft hat genau in der Stab­achse anzu­greifen und das im rechten Winkel zum Quer­schnitt.
  • Es dürfen keine anderen Kräfte oder Mo­mente vor­handen sein (zum Bei­spiel Wind­lasten).


In welchem Bereich die Sicher­heit gegen Knicken liegen sollte, kann man der folgenden Tabelle ent­nehmen:
 

  Sicherheit
Maschinenbau Stahlbau
 Euler 5 – 10 2.5
 Tetmajer 3 – 8 1.5

Werbung

Seite erstellt am 10.06.2019. Zuletzt geändert am: