Rechner für Knicken von Stäben (Euler & Tetmajer)

This page in English: Buckling of Columns (Euler and Tetmajer)

In der Technischen Mechanik bezeichnet man als Knicken das seitliche Ausweichen eines Stabes unter einer axialen Druckbelastung und das anschließende Versagen.

Mit diesem Online-Rechner können die Sicherheit gegen Knicken, die Knickdruckkraft (Knicklast), die Knickspannung und der Schlankheitsgrad λ von idealen Stäben berechnet werden, wobei die Last und die Querschnittsform bekannt sein müssen. Es werden die vier klassischen Eulerfälle berücksichtigt, wobei entweder nach Tetmajer (unelastischer Bereich) oder Euler (Hookescher bzw. elastischer Bereich) gerechnet wird.

Link zu Unterseite:

Formeln, Zahlenwerte und Hintergrundwissen für Knicken von Stäben

Rechner für Knicksicherheit & Knicklast von Stäben

Mit der Voreinstellung wird die Sicherheit gegen Knicken für einen idealen I-Träger (I100) aus S235 berechnet, wobei der zweite Eulerfall vorliegt. Die Knickkraft beträgt 10 kN und die Knicklänge 2 m.

Querschnitt
Höhe H	mm
Breite B	mm
Höhe h	mm
Breite b	mm

Werkstoff
Kraft F	kN
Eulerfall
Faktor β *
Stablänge l	m

Spannung σ_vorh	N/mm²
Knickspannung σ_K	N/mm²

Knicksicherheit S
Knickdruckkraft F_K	kN

Für Experten: Eingabe individueller & Ausgabe spezieller Werte

E-Modul	N/mm²
Koeff. a
Koeff. b ***
Koeff. c

R_e \| R_p0.2	N/mm²
λ_g
I_min **	cm⁴
Fläche A **	mm²

* Der Faktor β wird automatisch durch die Auswahl eines Eulerfalls eingetragen, kann jederzeit geändert werden.
** Um diese Werte eingeben zu können, wählt man unter Querschnitt –> Sonstige Profile –> “Eigenes Profil”.
*** Der Koeffizient b muss bei diesem Rechner normalerweise ein negatives Vorzeichen haben!

Hinweise

Die Koeffizienten a, b und c sind nur relevant, wenn die Berechnung nach Tetmajer erfolgt. Ob nach Euler oder Tetmajer gerechnet wird, hängt von der Grenzschlankheit λ_g ab, die bei Kenntnis von E-Modul und Streckgrenze R_e ermittelt werden kann, siehe Formel.
Die Berechnung erfolgt für idealisierte Profile, das heißt, schräge Kanten und Abrundungen werden nicht berücksichtigt!
Der Rechner geht von einem idealen Stab aus. In der Realität gibt es jedoch viele Imperfektionen, weshalb große Sicherheiten einzuplanen sind. Alternativ ist eine Berechnung nach DIN EN 1993-1-1:2010 (Eurocode 3) möglich – allerdings nicht mit diesem Rechner.
Dieser Rechner kann zum Beispiel auch dann verwendet werden, wenn die Kraft F bei gegebener Knicksicherheit gesucht ist: In diesem Fall bestimmt man die Lösung per Iteration.
Als Material stehen die beiden Baustähle S235 (St37) und S355 (St52), Grauguss EN-GJL-200, Aluminium ENAW-6082 und Fichtenholz zur Verfügung. Es ist zudem möglich, individuelle Werkstoffkennwerte einzugeben. Das minimale axiale Flächenträgheitsmoment und die Querschnittsfläche können entweder näherungsweise berechnet oder aber direkt eingegeben werden, wenn diese Werte aus Tabellen bekannt sind.

Erklärung der Abkürzungen und Einheiten

Dm	Durchmesser in mm
β	Faktor zur Berechnung von l_k, abhängig vom Eulerfall
l_k	Knicklänge; l_k = β × l (Stablänge) in m
σ_vorh	vorhandene Druckspannung im Stab; σ_vorh = F ÷ A; in N/mm²
σ_K	Druckspannung, bei der der Stab seitlich ausknickt; in N/mm²
F_K	Kraft, bei der der Stab seitlich ausknickt; in kN
S	Sicherheit gegen Knicken; S = F_K ÷ F
R_e	Streckgrenze in N/mm²
R_p0.2	0.2-%-Dehngrenze in N/mm²
λ_g	Grenzschlankheit: bestimmt, ob im vorliegenden Fall nach Tetmajer (unelastischer Bereich) oder Euler (Hookescher bzw. elastischer Bereich) zu rechnen ist.
I_min	Kleinstes axiales Flächenträgheitsmoment in cm⁴
A	Querschnittsfläche des Stabes in mm²
a, b, c	Koeffizienten für die Tetmajer-Gleichung; Koeffizient b benötigt im Regelfall ein negatives Vorzeichen!

Weitere Hinweise für die Verwendung des Rechners

Folgende Querschnittsflächen sind verfügbar:

Rundstange (Zylinder)
Rundrohr (Hohlzylinder)
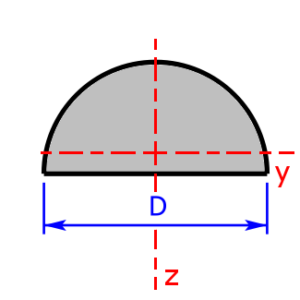
Halb-Rundstab
Rechteck-Profil

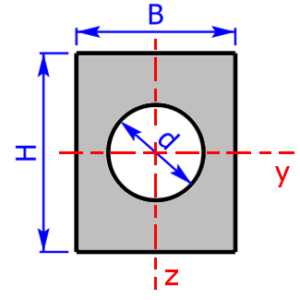
Rechteck mit Bohrung
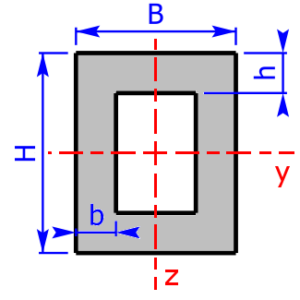
Rechteck-Hohlprofil
I- / H-Profil (Doppel-T-Träger)
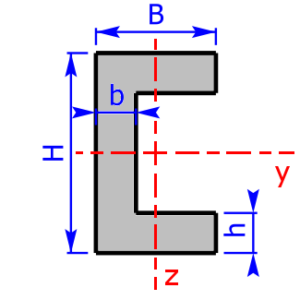
U- bzw. C-Profil

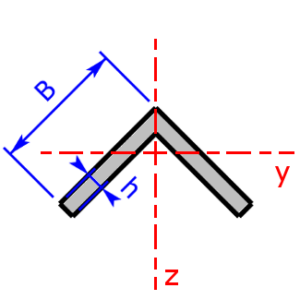
L-Profil (gleichschenkelig)
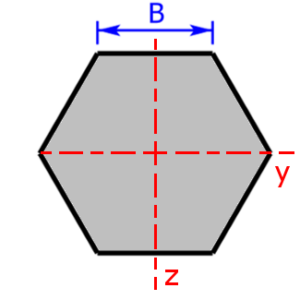
Sechseck/Sechskant
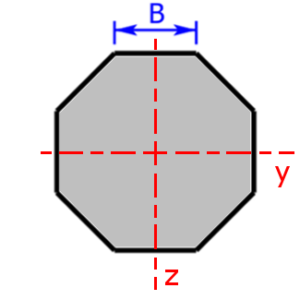
Achteck/Achtkant
Eigenes Profil

Im Maschinenbau sind die Sicherheiten ca. doppelt so hoch wie im Stahlbau zu wählen. Der Rechner verwendet die minimalen Sicherheiten vom Stahlbau. Man muss immer relativ große Sicherheiten einplanen, da die Berechnungen eigentlich nur für einen idealen Stab gelten:
- Die Kraft muss genau in der Stabachse angreifen und zwar im rechten Winkel zum Querschnitt.
- Der Stab wird als homogen angenommen; das heißt, er ist an jeder Stelle gleich beschaffen.
- Es darf keine anderen Kräfte und Momente geben, wie zum Beispiel Windlasten.
Die Querschnitte müssen immer symmetrisch zu den beiden Koordinatenachsen sein.
Im elastischen Bereich (Euler) knicken beim gleichen Aufbau (Lagerung, Querschnittsform und Länge) alle Stähle unter derselben Last, da sie den gleichen E-Modul besitzen!! Es hilft in diesem Fall z. B. nicht, wenn man einen Baustahl S355 statt S235 verwendet!
In der Praxis liegt oft Eulerfall 2 vor, da die übliche Befestigung am Boden nicht als feste Einspannung gewertet werden kann.
Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular!

Hintergrundwissen zum Rechner

Die vom Rechner verwendeten Formeln, Zahlenwerte (z. B. Werte für die Sicherheit) und weiteres Wissen finden Sie auf der folgenden Unterseite:

Formeln, Zahlenwerte und Hintergrundwissen für Knicken von Stäben

Welcher Stab knickt früher?

Ein Stab knickt bei Überschreitung der Knickdruckkraft. Die Knickdruckkraft ist umso größer, je größer das Flächenträgheitsmoment ist, da das Flächenträgheitsmoment I_min im Zähler der Formel steht:

$$F_K=\frac{\pi^2·E·I_{min}}{(\beta·l)^2}= \frac{\pi^2·E·I_{min}}{l_k^2} $$

Daher knickt bei den gleichen Lagerungsbedingungen und derselben Länge zuerst stets jener Stab, der das kleinere minimale Flächenträgheitsmoment hat (identer E-Modul vorausgesetzt). Die Knickdruckkraft hängt in diesem Fall also nur von der Form des Querschnitts ab.

Verwendung des Rechners:

Beliebige Länge, Eulerfall, Werkstoff und Kraft annehmen, da nur die Querschnittsfläche relevant ist.
Verschiedene Querschitte auswählen, eventuell Abmessungen anpassen und “Berechnen” drücken. Die jeweiligen Werte für die Knickdruckkraft bzw. die Knicksicherheit notieren.
Vergleichen der Knickdruckkräfte bzw. der Knicksicherheiten: Der Stab mit der kleineren Knickdruckkraft bzw. mit der kleineren Knicksicherheit knickt früher.